Cost Reduction in Supply Chain Management by Shorter Purchasing Lead-time: A Case Study of Flexible Printed Circuit Boards

INTRODUCTION

Supply Chain Management (SCM) encompasses materials/supply management from raw material to finished product (Tan et al., 1998). A supply chain contains four levels, supplier, manufacturer, distributor, and consumer, where each may be comprised of numerous facilities (Beamon, 1999).

A shorter lead-time implies better customer service, less inventory, and higher efficiency, and thus is more and more important for obtaining competitive advantage and increased market shares (Wedel and Lumsden, 1995). Taking made-to-order manufacturing as an example, 54% of the delivery time is waiting, which suggest that there is significant potential for improvement (Jahnukainen and Lahti, 1999).

The definition of a supply chain has changed along with the various technology breakthroughs seen in the last few decades. In the early and middle 1990’s, a supply chain was defined as a group of firms/organizations which function as a network flowing from raw material to final product or service (Ellram, 1991). With the rise of the Internet, business entities within the supply chain became more strategically allied and began to exchange more information to accelerate business processes.

Disregarding the finer points of these changes in definition, a supply chain is commonly seen as being organized into several groups for specific purposes, which are raw material supplier, sub-component supplier, assembler/manufacturer, distribution providers, and customer/consumer (Thomas and Griffin, 1996; Kopczak, 1997). Beamon (1999) defined that a supply chain contained the suppliers, manufacturers, distributors and consumers, and they were grouped differently depending on whether they play as a supplier, producer, wholesaler, or retail outlet.

Shin et al. (2000) constructed a supply chain measurement model in terms of supplier and buyer performance. Supplier performance includes cost, quality, delivery reliability, lead-time, and on-time delivery. Beamon (1998) presented a different measurement approach based on both qualitative and quantitative aspects. Furthermore, Beamon (1999) also identified output and flexibility as the major performance measurements. Accordingly, most of the available performance measurement models have been cost-related. Lawrence (1999) argued that the cost of safety stock and stock out were influenced by lead-time and variability, as well as the results of Gilbert and Ballou (1999) study. In addition, Tyworth and Zeng (1998) found that the expected total annual logistics cost is the sum of transportation, holding, ordering, and shortage costs, in which transportation cost is further related to the freight rate, annual demand, and weight of goods. The application of SCM or cost reduction is often found in the management literature (Ahmadi and Teimouri, 2008; Ebrahimipoor et al., 2009; Emongor and Kirsten, 2006; Hemalatha and Vivekanandan, 2008; Kocsoy et al., 2008; Lee et al., 2008; Alqedra et al., 2011; Reaz et al., 2009; Shafia et al., 2009; Shirazi et al., 2008).

The aim of this study was to understand how purchasing lead-time at the manufacturing level influenced the overall cost of the supply chain. A cost model constructed in this study was used to analyze the effects arising from a reduction in purchasing lead-time. Furthermore, a case study of flexible Printed Circuit Boards (PCB) was included to illustrate this approach.

THE OPTIMAL EXPECTED TOTAL COST REDUCTION MODEL

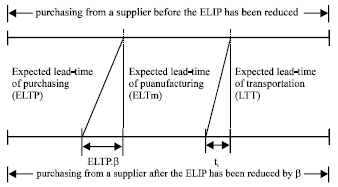
This study investigates how a manufacturer can reduce the costs resulting from the vendor’s delivery lead-time which is identical to manufacturer’s purchasing lead-time. Utilizing the proposed optimal expected total cost reduction model, guidelines are developed for an incentive program in which vendors will be motivated to reduce the lead-time for each purchase. This model is constructed under the following conditions (1) material will be brought solely from a single vendor, (2) the quality of material from this vendor is acceptable and constant, (3) the vendor is able to reduce the purchasing lead-time at a constant ratio of β (0≤β≤1) when encouraged by the incentive program, (4) the quality of products manufactured is acceptable and constant and (5) the manufacturer has to use the fastest transportation method to ensure on-time delivery. The Expected Delivery Time (EDT) of a manufacturer in a supply chain is composed of the following three major elements, as shown in Fig. 1:

•	Expected lead-time of purchasing (ELTP): The expected time frame from placing an order to the receipt of raw material
•	Expected lead-time of manufacturing (ELTM): The expected time frame from the receipt of material to the finished products being shipped
•	Lead-time of transportation (LTT): The time frame from shipment to the receipt by customers

The top of Fig. 1 represents the EDT of a manufacturer that purchases from a supplier with the regular ELTP.


Fig. 1:	The structure of manufacturer’s expected delivery time (EDT)

The bottom represents the EDT of a manufacturer who purchases from the same supplier after conducting ELTP reduction by β. In order to objectively compare the manufacturer’s cost of purchasing from the same supplier before and after this reduction, the manufacturer’s EDTs remain identical, regardless of the changes in the ELTP. As a result, when the manufacturer purchases from a supplier with reduced ELTP, the ELTM and/or the LTT tend to have more flexibility to respond to the changes in the schedule.

The following symbols and notations used throughout this study are as follows:

b	:	Direct labor cost (amount per thousand units)
C	:	Cost of the material (amount per item)
D	:	Annual demand of the material (units per year)
d	:	Daily demand of the material (units per day)
E_(Z)	:	Unit normal loss integral
e	:	Equipment depreciation (amount per thousand units)
F_i	:	Freight rate of approach i where i = 1, 2, 3, …, n (amount per kg)
I	:	Holding cost (expressed as a percentage of the item cost)
k	:	Stock out cost (amount per order)
P	:	Daily shipment (thousand units per day)
Q	:	Economic Order Quantity (EOQ) after the ELTP has been reduced by β (units per order)
q	:	Economic Order Quantity (EOQ) before the ELTP has been reduced (units per order)
S	:	Ordering cost (amount per order)
s	:	Working days (days per year)
T_i	:	Transportation lead-time for approach i where i = 1, 2, 3, …, n (days)
t_i	:	Increased transportation lead-time, compared with the first approach when using approach i where i = 1, 2, 3, …, n (days)
w	:	Weight per thousand units (kg)
Z	:	The number of standard deviation
β	:	Lead-time reduction ratio for each purchase (percentage)
σ²_d	:	Variance of daily material demand
σ²_LTP	:	Variance of purchasing lead-time
λ	:	Daily demand of product (thousand units per day)
μ	:	Daily production capacity (thousand units per day)
μ_i	:	Daily production capacity when using transportation approach i (thousand units per day)

When the EDT remained, any changes in ELTP, ELTM and LTT might influence the total cost. For a given β, the reduced lead-time is (1-β) ELTP and the standard deviation and variance are (1-β)σ_LTP and (1-β)² σ²_LTP, respectively. The above change will result in (1) cost reduction in relevant inventory, (2) cost reduction in transportation method and (3) cost reduction in capacity.

The effect of a reduction in ELTP on expected relevant inventory cost: The influence of a reduction in ELTP on the inventory cost is explored in this subsection where the cost structure is based on the following assumptions:

•	The demand is continuous and given
•	The purchasing lead-time and demand are both based on normal distribution
•	The ordering cost is constant
•	The back order is not allowed
•	The holding cost is linear and
•	The lead-time can be reduced by a ratio of β for each purchase

Based on the relevant cost model presented by Lawrence (1999) and Ballou (1992), the following equations are developed by this study where the Expected Relevant Inventory Cost (ERIC) before ELTP reduction can be obtained as follows:

(1)

where, q (EOQ) is:

(2)

and Safety Stock (ss) is:

(3)

According to Eq. 1, the first term is the cost of order processing, where the period can be of any length. However, it must be long enough to last through a purchasing cycle. Yearly demand is a common choice for this cycle which can be divided by q (EOQ) to obtain the number of orders placed in a year. In the second term, the cost of holding average inventory is presented where q divided by two represents average inventory. The next term is the cost of holding safety stock. The final term is the cost of stock outs, where the combined term of:

represents the expected numbers of stock outs during an order cycle. When Z is 1.645 for the desired service level of 95%, E_(Z) is then equal to 0.0211 (Ballou, 1992).

According to the above when the purchasing lead-time is reduced by β for each purchase, the ERIC, q, and ss would be reformulated as follows:

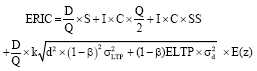(4)

where, Q (EOQ) is:

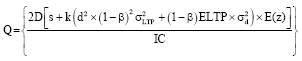(5)

and Safety Stock (SS) is:

(6)

When comparing Eq. 1 and 4, one can see that when the ELTP is reduced, EOQ will also decrease. This thus results in an increase in the cost of order processing and a decrease in the cost of holding average inventory. In addition, the reduction in both ELTP and variance will cause the cost of holding safety stock and stock outs to decrease.

Based on the above, if provided with the purchasing lead-time reduced by β for each purchase, the Expected Cost Reduction of Relevant Inventory (ECRRI) can be obtained by subtracting Eq. 4 from 1, as follows:

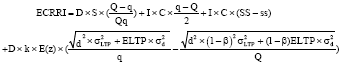(7)

In Eq. 7, the q, ss, Q, and SS are those stated in Eq. 2, 3, 5 and 6. The first term presents the cost difference of orders processing in Eq. 4 and 1 which is always a negative value to illustrate the increasing cost.

The effect of a reduction in ELTP on transportation cost: According to Tyworth and Zeng (1998), the freight rate and weight affect the transportation cost. The assumptions of transportation are as follows:

•	The transportation cost is weight related
•	The freight rate is based on transportation time which normally requires more money to deliver with in a shorter time, and
•	There are n available transportation methods

According to the above, the first transportation method (T₁), the most expensive and fastest way to deliver products, has been normally selected to avoid any delay. The reduction in transportation cost comes from extra transportation time being allowed, which results from the reduced ELTP, provided there is a fixed EDT. The extra transportation time obtained, t_i, can be expressed as:

(8)

where, LTT_i is the lead-time of transportation approach i.

Accordingly, t_i can be employed to utilize other flexible transportation approaches with less cost. The Cost Reduction of Transportation approach i (CRT_i) can be formulated as the equation below, which also uses the most expensive freight rate, F₁ as the basis for comparisons:

(9)

where, s is the number of working days in a year.

When a transportation approach with less cost is adopted, a cost benefit, CRT_i, can be achieved. The optimal approach i happens while the sum of CRT_i and the Expected Cost Reduction of Capacity for approach i (ECRC_i) reaches a maximum value.

The effect of a reduction in ELTP expected capacity cost: The required production capacity can be analyzed based on the M/M/1 queuing model presented by Gilbert and Ballou (1999). The assumptions of the queuing model are as follows:

•	The processing times are exponentially distributed
•	The arrival of material is a Poisson process
•	There is only one set of production equipment available and
•	The finished products must be shipped instantly

According to the M/M/1 queuing model, the ELTM can be obtained as follows:

(10)

then,

(11)

As shown in Fig. 1, based on the ELTP being reduced by a ratio of β and the LTT increased by t_i, the Expected Lead-Time of Manufacturing for approach i (ELTM_i) can be formulated as follows:

(12)

Assuming constant demand, the following equations can be derived using the M/M/1 queuing model and daily production capacity for approach i (μ_i) can be obtained with the following equation:

(13)

Replacing ELTM_i in Eq. 13 for that in Eq. 12 when ELTP is reduced by a ratio of β and LTT is increased by t_i, Eq. 13 can be further updated to:

(14)

From Eq. 11 and 14, the following can be obtained:

(15)

where, Δμ_i refers to the reduction in capacity for approach i.

Maintaining the excess capacity leads to cost increases due to production equipment, labor force, and storage space (Lawrence, 1999). Since the cost of space is very difficult to measure, only equipment and direct labor costs are considered in this study. The ECRC_i can thus be obtained, as follows:

(16)

In Eq. 16, multiplying the reduction of capacity for approach i (Δμ_i) by the sum of unit equipment and direct labor cost (e+b) gives the daily capacity cost reduction for approach i. Replacing the Δμ_i in Eq. 15 for that from 15, then:

(17)

From Eq. 17, the equipment investment and labor cost are reduced when the ELTM increases.

The optimal expected total cost reduction modeling: Based on the above equations derived, lead-time reduction ratio, β, for each purchase will lead to cost reductions for ECRRI, CRT_i and ECRC_i. From Eq. 7, 9 and 16, the Expected Total Cost Reduction of approach i (ETCR_i) in a year can be obtained. Furthermore, the Optimal Expected Total Cost Reduction (OETCR) in a year resulting from ELTP reduction, when using approach i, is given as follows:

(18)

Subject to

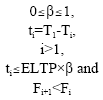In the Eq. 18, there is a trade-off between CRT_i and ECRC_i. The longer the t_i is, the greater the OETCR becomes. Since the growth of ECRC_i is limited, only one t_i exists for a given OETCR. If the first approach has been selected, the reduced ELTP can be achieved by utilizing ECRC_i instead of CRT_i.

CASE STUDY

A flexible Printed Circuit Board (PCB) manufacturing company located in Taiwan, which is a supplier to notebook PC, printer, hard disk drive, and digital camera manufacturers, has been investigated to verify the proposed approach. Similar to other electronic companies, the subject company has to deal with short delivery times and rush orders, which often results in excess inventory and capacity. Accordingly, the subject company would like to aggressively reduce the ELTP to pursue more cost effective operations.

Optimal expected total cost reduction model solution: The flexible PCB production flow is shown in Fig. 2 which includes design, front processes, patterning, lamination, surface treatment, and back processes. During the patterning process, etching has always been a bottleneck due to low yield. Cover lay is the main raw material, which has to be purchased in rolls. The subject company’s detailed information is listed in Table 1.

As to the CRT_i, it takes 1.6 rolls of cover lay for every 1,000 pieces output. Accordingly, 12.8 rolls are needed for the daily 8,000 output, 281.6 rolls for monthly (22 working days) production, and 3,380 rolls for annual demand (D). Based on Eq. 12, the EOQ can be obtained as 30 rolls. As mentioned before, if the desired service level is 95%, then, the Z and E_(Z) are 1.645 and 0.0211, respectively. As to the stock out cost per order (k), three scenarios are presented. First, the customer requests a stock out item and is willing to wait based on the regular lead-time. Second, the customer requests a stock out item and is unable to wait for the regular lead-time, and so the company has to initiate an expedited order. Third, the sale will be lost when the material is stock out (Lawrence, 1999).


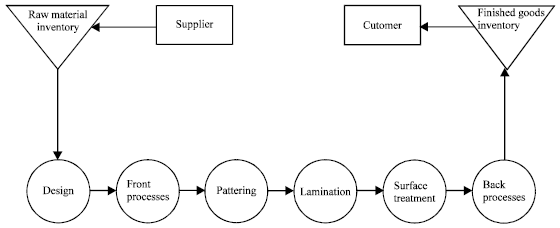Fig. 2:	The Supply Chain of the Flexible PCB Processing

Table 1:	Information about the Flexible PCB manufacturing company

Table 2:	The ECRRI in different β levels

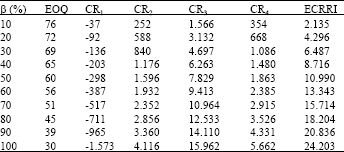CR₁: Cost reduction of orders processing; CR₂: Cost reduction of holding average inventory; CR₂: Cost reduction of holding average inventory; CR₄: Expected cost reduction of stock out

In case of the first and second scenarios, the added ordering costs will be 20 and 50%, respectively. Under the third circumstance, the cost of the lost sale for the company is $1,000. Based on the Table 1, the expected stock out cost is equal to $108.58, considering the probability for each scenario provided. Accordingly, Eq. 14 is used to obtain the ECRRI for different β, and these are summarized in Table 2.

As for the ECRC_i, air freight is used to transport products from Taiwan to Japan in order to meet limited time frame. The product weighs two kgs per 1,000 pieces. There are three approaches to be considered. The freight rate of the first is $8.696 (F₁) per kg, which takes only two days (T₁); the second is $6.667 (F₂) per kg, with three days (T₂) needed; and the third is $5.507 (F₃) per kg in four days (T₃). Therefore, the CRT_i of each transportation approach for different β can be obtained with Eq. 9.

As for the ECRC_i, if the daily output (λ) is 8,000 pieces, this is also number of the shipping units. To manage rush orders and variations in quality, the daily capacity (μ) has to be increased to the level of 12,000 pieces, which results in an ELTM of 0.25 day in Eq. 10.

Table 3:	Maximum cost reduction of i for different β levels

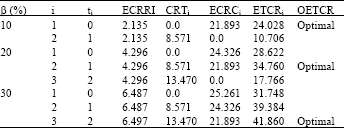β: Percentage of lead-time reduction ratio for each purchase

Table 4:	Scenarios analysis of case study

β: Percentage of lead-time reduction ratio for each purchase; R*: Percentage of the OETCR to total annual purchased amount ($2,028,000)

Since the manufacturing equipment costs $85,000 and the depreciation period is three years, the equipment cost per 1,000 pieces share (e) is $13.415. Under current operational arrangements, the equipment requires five operators with a wage of $20 per operator per day. The direct labor cost per 1,000 pieces (b) is thus equal to $12.5. As a result, the ECRC_i of each transportation approach for different β can be obtained from Eq. 17.

Consequently, given the ELTP reduction ratio, β, the variance can be lowered proportionally. By substituting β with 10, 20, and 30% in Eq. 18, Table 2 can be obtained, where the ETCR_i reaches its most cost-effective status with 10% ELTP reduction when i equals one. As β becomes 20 and 30%, the maximum ETCR_i (OETCR) occurs when i is equal to two and three, respectively. Table 3 also reveals a trade-off between ECRC_i and ECRC_i. When β equals 10%, if the one day saving in ELTP can be applied to the ECRC_i, the cost can be reduced by $21,893 while the CRT_i reduces it by only $8,571. When utilizing the time saved in ECRC_i, an i equal one becomes the most cost effective option when β equals 10%. Accordingly, it also results in i equals two and three with a β of 20 and 30%, respectively, to achieve a similar outcome. More information about i with different levels of β is given in Table 4.

Vendor policy: The vendor can usually be motivated to reduce the lead-time for each purchase through the utilization of the proposed total cost reduction model. For a manufacturer, the ELTP varies from one vendor to another, and thus different cost reductions can be achieved.

Table 5:	Sensitivity analysis in OETCR

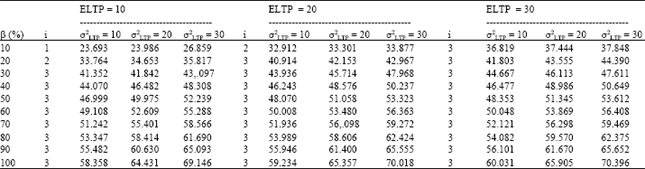β: Percentage of lead-time reduction ratio for each purchase

Table 6:	Sensitivity analysis in R^*

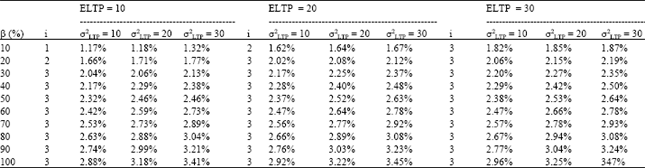β: Percentage of lead-time reduction ratio for each purchase

R* the maximum benefit ratio from ELTP reduction, provides a reference for the manufacturer to share profits with suppliers. As to vendor policy, an incentive feedback program is worth establishing. Table 4 offers the feedback guidelines with respect to various vendors’ time reductions for delivery to encourage continuous improvement. Moreover, vendors can use these guidelines to enhance their managerial and manufacturing performance in order to obtain incentives from a reduction in ELTP.

Sensitivity analysis: The sensitivity analysis is used to explore the major factors of cost reduction when the ELTP is reduced at different levels of β. ELTP and variance reduction against cost reduction is presented by assuming that both ELTP and variance have three levels of 10, 20, and 30. In Table 5 and 6, the cost reduction and reduced ratios are listed. In Table 6 it can be seen that the cost reduction is mainly influenced by ELTP with a lower β. Taking β at 10% and ELTP at 20 as an example, the cost reduction rates under different variance levels are 1.62, 1.64, and 1.67, respectively, which demonstrate similar results. On the other hand, as to a fixed σ²_LTP of 20 with different ELTP at 10, 20, and 30, the cost reduction rates are 1.18, 1.64 and 1.85, respectively. Accordingly, the cost reduction depends mainly on the ELTP, to which β makes only a minor contribution.

In contrast, with the same ELTP level of 20 with β at 100%, the cost reduction rates are 2.92, 3.22, and 3.45 at various σ²_LTP levels. In addition, as to a fixed σ²_LTP of 20, the cost reduction rates are 3.18, 3.22, and 3.25 when β is equal to 100% for different ELTP levels. Accordingly, the cost reduction is mainly affected by the variance of the ELTP instead of ELTP itself when β is close to 100%. When β increases, the variance decreases dramatically, which also leads to a significant improvement in ECRRI. Furthermore, CRT_i and ECRC_i are mainly affected by the reduced ELTP.

Although β can increase up to 100%, there exists only three possible transportation approaches, which limit the reduction scale of CRT_i. In addition, it is clear that ECRC_i can not be improved significantly based on the results of scenario analysis. The situation described above can be explained by Table 4, where the ECRRI is mainly influenced by the reduction in variance, while the CRT_i and the ECRC_i are mainly influenced by the ELTP.

CONCLUSIONS

This study focuses on variation in supply chain cost when the ELTP can be reduced with the required EDT unchanged. An illustrative case study of a flexible PCB company validates the proposed model through sensitivity analysis. The following conclusions can be presented:

•	With regard to the cost reduction, a reduction in ELTP leads to lower expected total cost, which jointly comes from the reductions in expected relevant inventory cost, transportation cost, and expected capacity cost
•	There exists a trade-off between transportation cost and expected capacity cost

Overall, an improved ELTP can reduce manufacturing cost, and the savings cab be shared with vendors through an incentive feedback program. Accordingly, the total cost in the supply chain tends to become lower, which will definitely enhance firm competitiveness.

ACKNOWLEDGMENTS

This study is partially supported by the National Science Council of Taiwan under grant NSC 94-2416-H-218-008.