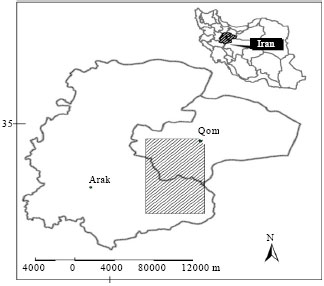
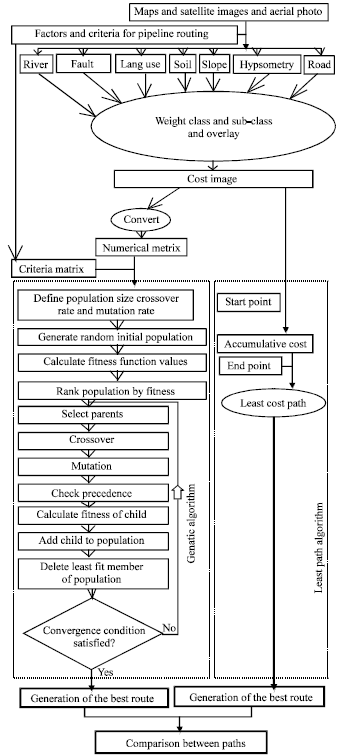
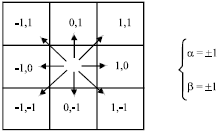
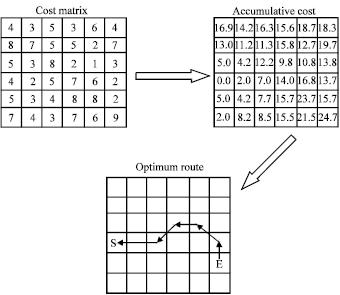
Research Article
Routing of Water Pipeline Using GIS and Genetic Algorithm
Academic Center for Education, Culture and Research, Tarbiat Moallem Branch, No. 49, Mofatteh Avenue, Tehran, Iran
A. Alimohamadi
Department of GIS, Faculty of Geodesy and Geomatics Engineering, K.N. Toosi University of Technology, Tehran, Iran
A.A. Alesheikh
Department of GIS, Faculty of Geodesy and Geomatics Engineering, K.N. Toosi University of Technology, Tehran, Iran
H. Aghighi
Department of GIS, Faculty of Geodesy and Geomatics Engineering, K.N. Toosi University of Technology, Tehran, Iran
LiveDNA: Iranian Space Agencies, Tehran, Iran