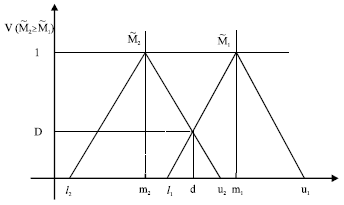
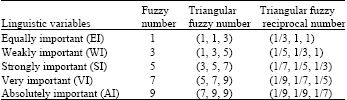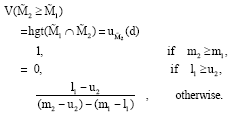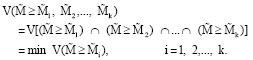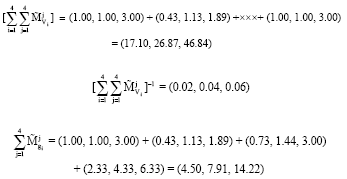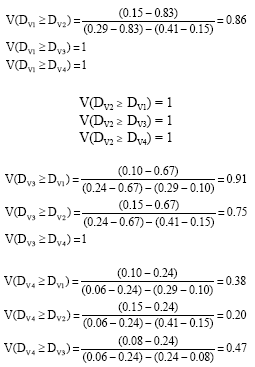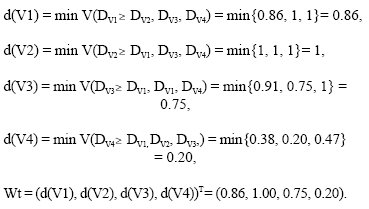Research Article
Combing Fuzzy Set Theory and Extent Analysis to Construct an Integrated Decision Making Approach in Medical Cosmetology Industry
Department of Industrial Education and Technology, National Chunghua University of Education, Bao-Shan Campus, No. 2, Shi-Da Road, Changhua City, Taiwan, Republic of China
Kai-Fu Yang
Department of Industrial Education and Technology, National Chunghua University of Education, Bao-Shan Campus, No. 2, Shi-Da Road, Changhua City, Taiwan, Republic of China