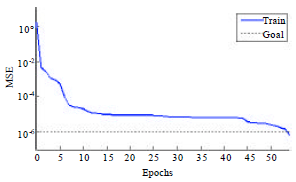
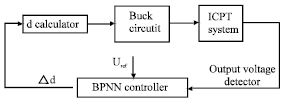
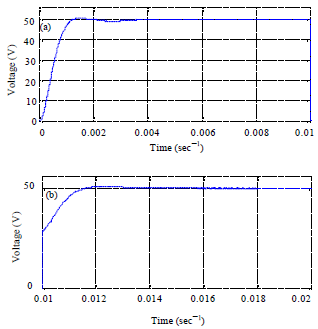
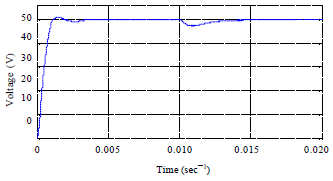
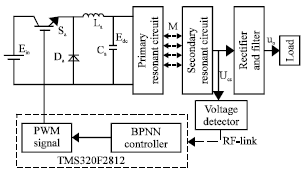
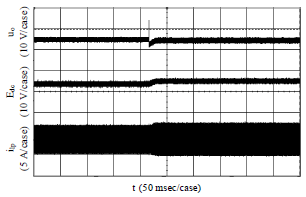
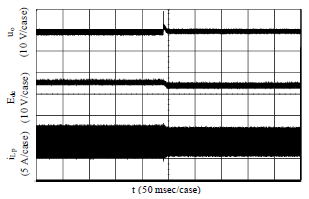
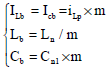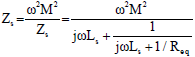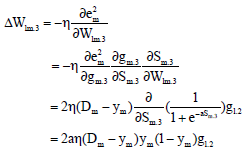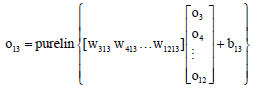Research Article
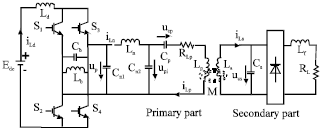
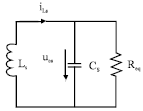
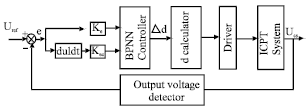
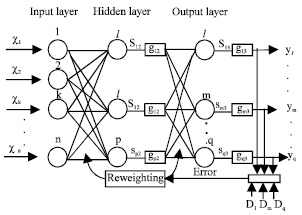
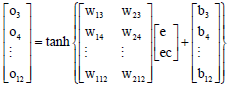
Study on Voltage-stabilizing Control of ICPT System
College of Automation, Chongqing University, Chongqing 400030, China
Yue Sun
College of Automation, Chongqing University, Chongqing 400030, China
Yong Tian
College of Automation, Chongqing University, Chongqing 400030, China
Fangxun Yang
College of Automation, Chongqing University, Chongqing 400030, China
Yugang Su
College of Automation, Chongqing University, Chongqing 400030, China