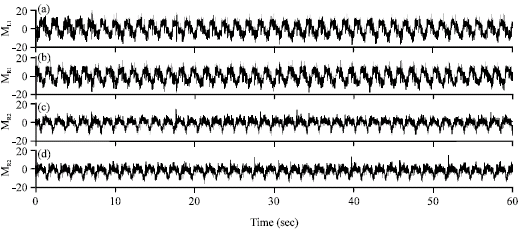
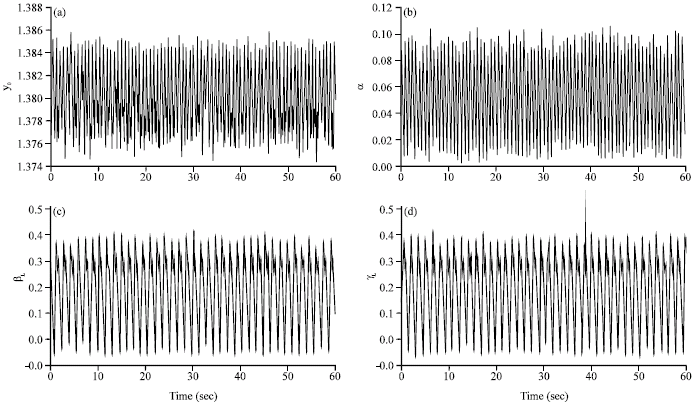
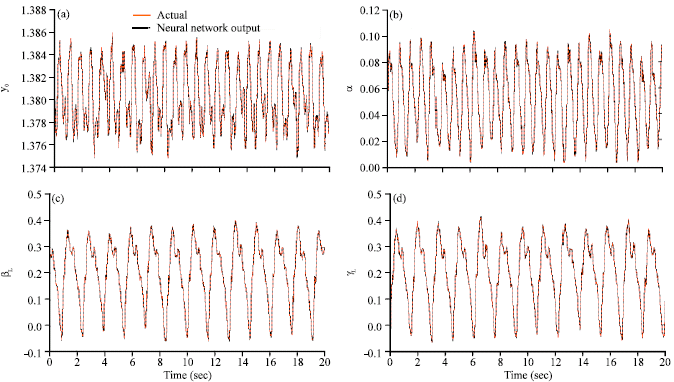
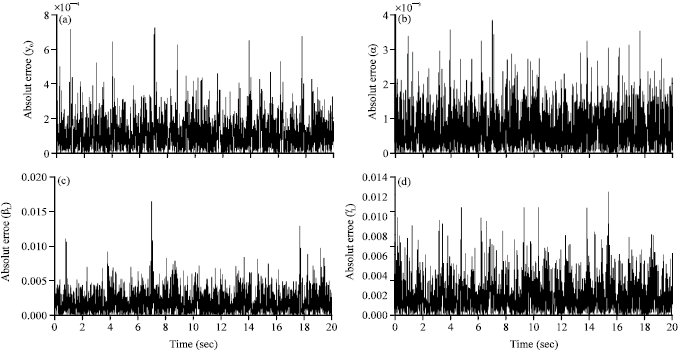
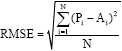Research Article
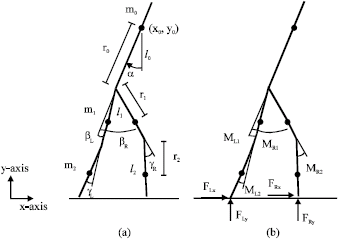
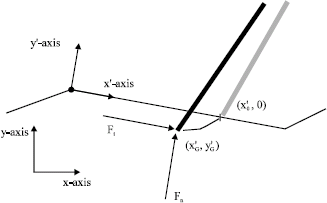
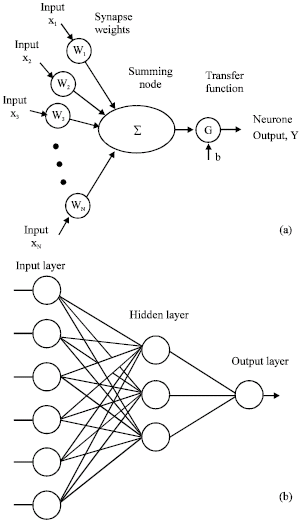
Modeling of a Five-Link Biped Robot Dynamics Using Neural Networks
Department of Electrical Engineering, Imam Khomeini International University, Qazvin, Iran
K. Afshar
Department of Electrical Engineering, Imam Khomeini International University, Qazvin, Iran
B.I. Lame
Department of Electrical Engineering, Imam Khomeini International University, Qazvin, Iran
A. Zohrabi
Department of Electrical Engineering, Imam Khomeini International University, Qazvin, Iran