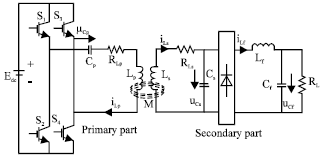
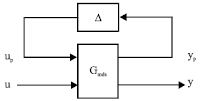
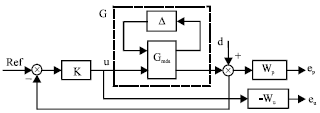
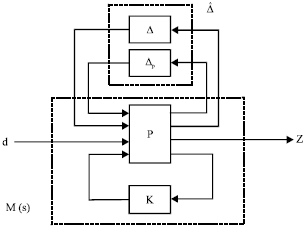
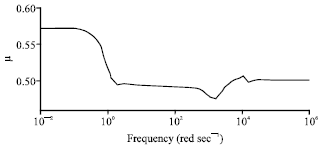
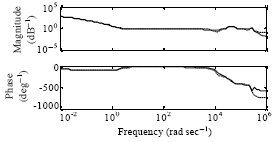
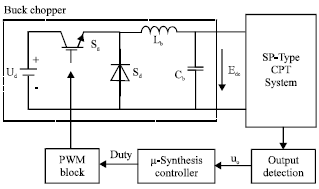
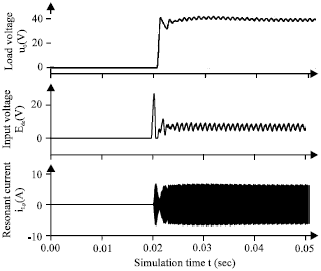
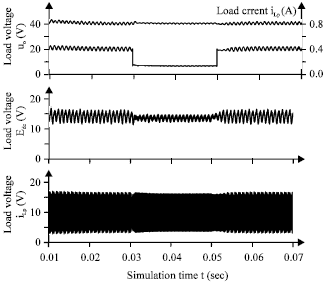
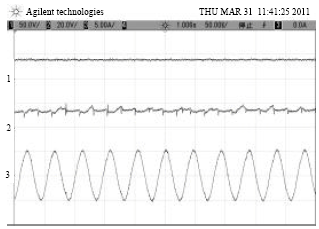
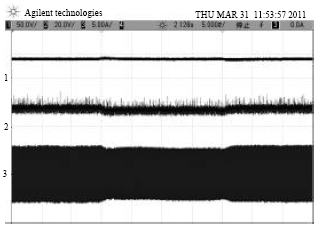
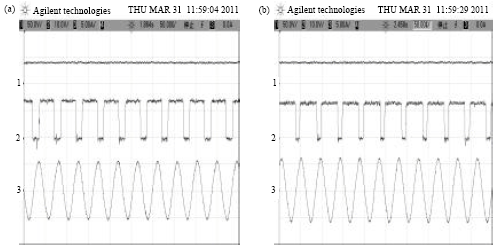
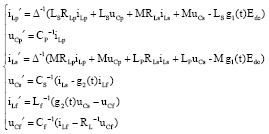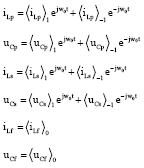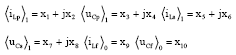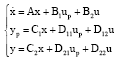Research Article
Controller Design for an Uncertain Contactless Power Transfer System
College of Automation, Chong-Qing University, Chong-Qing, China
Yue Sun
College of Automation, Chong-Qing University, Chong-Qing, China
Xin Dai
College of Automation, Chong-Qing University, Chong-Qing, China