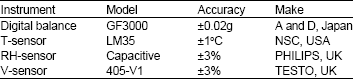
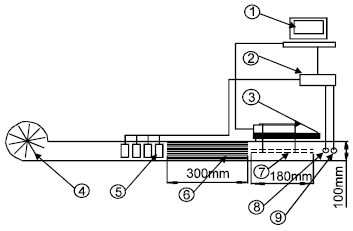
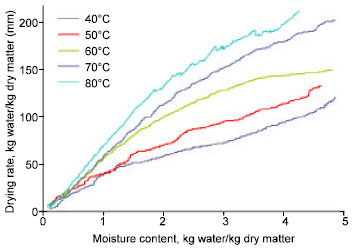
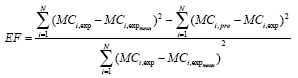Research Article
Moisture Content Modeling of Sliced Kiwifruit (cv. Hayward) During Drying
Department of Agricultural Machinery Engineering, Faculty of Bio - Systems Engineering, University of Tehran, Karaj, Iran
Shahin Rafiee
Department of Agricultural Machinery Engineering, Faculty of Bio - Systems Engineering, University of Tehran, Karaj, Iran
Alireza Keyhani
Department of Agricultural Machinery Engineering, Faculty of Bio - Systems Engineering, University of Tehran, Karaj, Iran
Zahra Emam - Djomeh
Department of Food Science and Engineering, Faculty of Bio - Systems Engineering, University of Tehran, Karaj, Iran