ABSTRACT
The Vapour Absorption Refrigeration System (VARS) has generated renewed interest and is being viewed as one of the alternatives for vapour compression refrigeration due to its potential for waste heat utilization. To improve the efficiency of these systems, it is necessary to study heat and mass transfer processes in absorption system components. The absorber, one of the crucial components in VARS is considered for study. Experimental investigation is carried out to study heat and mass transfer characteristics in a glass absorber. A new combination of R134a/DMF is used as the working fluid to overcome the limitations of well known working pairs, ammonia-water and lithium bromide-water. The effects of parameters viz., gas flow rate, solution initial concentration, solution pressure and solution temperature on absorber performance are analyzed. Heat and mass transfer coefficients evaluated from the experiments are compared with the numerical model and it is found that agreement is good. Heat and mass transfer coefficients increase as the gas flow rate, solution initial concentration and solution temperature increase whereas they decrease as the solution pressure increases. Sherwood number and Nusselt number evaluated from the experimental data are compared with those obtained from the numerical correlations developed earlier by the authors.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2011.1921.1928
URL: https://scialert.net/abstract/?doi=jas.2011.1921.1928
INTRODUCTION
Fulfillment of refrigeration requirements through low-grade waste heat recovery is part of the drive for the reduction of electrical energy consumption and optimal usage of resources. Intensive research has been focused in the absorption refrigeration technology, since it uses waste heat as energy source. Many environment friendly fluid combinations have been suggested by number of investigators in order to overcome some of the limitations of well known working pairs viz., ammonia-water and lithium bromide-water for the VARS. Though HCFC refrigerant R22-organic solvent based absorption refrigeration systems have been extensively studied by Fatouh and Srinivasa Murthy (Fatouh and Murthy, 1995; Fatouh and Murthy, 1996a-c), HCFCs along with CFCs, are also covered by Montreal and other International Protocols and are being phased out. So environment friendly HFC refrigerant R134a based VARS are being investigated. Nezu et al. (2002) examined the possibility of testing R134a as a refrigerant in VARS with various organic solvents and showed that R134a-DMA and R134a-DMF systems are considered attractive as the working-fluid pairs for the absorption refrigeration system than other R134a/absorbent systems. Yokozeki (2005) studied the theoretical performance of various refrigerant-absorbent pairs in a VARS cycle by the use of equations of state. Of these, R134a-DMF and DMA systems exhibit better performance, compared to other R134a-absorbent systems. Also circulation ratio is less and COP is more for the R134a-DMF system compared to R134a-DMA system. Mani (2009) carried out experimental studies on R134a/DMF based compact vapour absorption refrigeration system with plate heat exchangers. He reported that this system could be very competitive for applications ranging from -10 to 10°C, with heat source temperature in the range of 80 to 90°C and with cooling water as coolant for the absorber and condenser in the temperature range of 20 to 35°C.
The absorber is considered as one of the crucial components in vapour absorption refrigeration system. Kang et al. (2000) carried out an analytical investigation of falling film and bubbles type absorbers and found that the absorption rate of bubble type absorber is found to be always higher than that of the falling film mode. Bubble type absorber provides better heat and mass transfer coefficients, also good wettability and mixing between the liquid and vapour.
Absorption process is characterized by simultaneous heat and mass transfer phenomena. These mechanisms, though complicated, influence the system performance significantly. Elperin and Fominykh (2003) studied the combined heat and mass transfer mechanisms at all stages of bubble growth and rise in a bubble absorber, which can be useful in the design calculations of gas-liquid absorbers. Lee et al. (2003) performed both numerical and experimental analyses in the absorption process of a bubble absorber. Numerical model in these studies can be used for the optimum design of absorber. Merrill and Perez-Blanco (1997) developed an analytical model to predict the bubble dynamics in binary sub-cooled solutions. This model improves the understanding of bubble absorption dynamics.
Sujatha et al. (1997a, b) carried out numerical analysis in a vertical tubular bubble absorber working with R22 as refrigerant and five organic fluids namely DMF, DMA, DMETEG, DMEDEG and NMP as absorbents. The model is validated by comparing with the results available in literature. Based on these results, a correlation for mass transfer coefficient has been suggested for the vertical tubular bubble absorber. Sujatha et al. (1999) also carried out experimental studies on a vertical tubular bubble absorber working with R22-DMF. The experimental pressure drop, heat transfer coefficient and mass transfer coefficient are compared with the results obtained from the numerical model.
Kang et al. (1998) developed a model for bubble absorber with a plate type heat exchanger by considering the combined heat and mass transfers analysis in both liquid and vapour regions. All geometric variables such as distance between the two plates, number of plates and width of the plates could be selected optimally for the given thermal conditions by the developed design model for ammonia-water combination.
Staicovici (2000a-c) used non-equilibrium phenomenological theory to evaluate the gas-liquid interaction. The design of bubble absorber, based on non-equilibrium thermodynamics could be suited to a modern compact plate type construction and offer better absorption efficiency and minimum pressure loss on the gas side. Suresh and Mani (2010) developed a numerical model on bubble dynamics, heat and mass characteristics of R134a/DMF based bubble absorber using phenomenological theory and validated the model by comparing with the results available in the literature.
Kang et al. (2002a) developed an experimental correlation of mass transfer coefficient for ammonia-water bubble absorption. They (Kang et al., 2002b) also developed a correlation for initial bubble diameter, which can be used to calculate the interfacial area in the design of ammonia-water bubble absorber. Cerezo et al. (2009) carried out experimental studies using a plate heat exchanger as absorber and ammonia water as working fluid. They concluded that increase in pressure, solution and cooling flow rates positively affects the absorber performance and increase in the concentration, cooling and solution temperature negatively affects the absorber performance.
The present experimental work is carried out to evaluate the heat and mass transfer coefficients and study the effect of parameters viz., gas flow rate, solution initial concentration, solution pressure and solution temperature on the performance of R134a/DMF bubble absorber.
MATERIALS AND METHODS
Schematic diagram of the experimental setup has been illustrated in Fig. 1. The setup consists of a glass bubble absorber, strong and weak solution tanks, solution pump, cooling water thermostat, instrumentation and valves. The glass absorber consists of two concentric tubes. DMF solution is pumped from weak solution tank, through the bottom of inner tube by a solution pump. R134a gas is supplied from a high pressure cylinder through a mass flow controller unit and injected through a nozzle installed at the bottom of inner tube. Strong DMF solution is collected in the strong solution tank at the top of the absorber. Cooling water is supplied by cooling water simulator, through absorber annulus counter flow to the solution and gas. Cooling water simulator consists of a R22 based Vapour Compression Refrigeration (VCR) circuit of 3.4 TR capacity, a cooling water tank insulated with Expanded Polyethylene (EPE) sheets, electric heaters, pump, flow meter, PT100 sensor, PID temperature controller, contactor, piping and valves. VCR circuit consists of a hermetically sealed reciprocating compressor, an air cooled condenser, a thermostatic expansion valve and cooling coil.
The location of various temperature sensors, pressure sensors, flow meters and valves are indicated in Fig. 1. All these measuring instruments are pre-calibrated. 12 numbers of copper-constant thermocouples are used as temperature sensors with a measurement uncertainty up to±0.5°C. 3 numbers of piezo-electric type pressure transducers are used as pressure sensors with a measurement uncertainty up to ±1.2%. Glass rotameters are used to measure the flow of solution and cooling water with a measurement uncertainty up to±2.5%. Mass flow controller unit is used to measure the volume flow rate of gas with a measurement uncertainty of±1%. An online density meter is used to measure the density of strong and weak solutions with a measurement uncertainty of ±0.1%. Concentrations of strong and weak solutions are evaluated from the measured density values using HBT (Hankinson-Brobst-Thomson) equation used by Reid et al. (1989).
 | |
| Fig. 1: | Schematic diagram of glass bubble absorber experimental setup |
Readings from all these instruments and sensors are monitored continuously by connecting them to a data acquisition system and a computer.
Initially DMF solution is charged into the weak solution tank. Then it is pumped through the inner tube of glass absorber by solution pump. Solution is collected in the strong solution tank at the top of the absorber. Solution is returned to the weak solution tank through a needle valve, after completion of one run of experiment. Initial concentration of the solution at the absorber inlet is measured by online density meter. Solution inlet pressure and temperature are monitored continuously and kept constant. Cooling water is allowed at a constant flow rate, through the outer tube of the glass absorber, counter flow to the solution. Then R134a gas is injected from a high pressure cylinder through the nozzle at the bottom of the absorber. Gas flow rate is accurately measured by the mass flow controller unit. Gas temperature is maintained constant. During this process, by keeping solution flow rate constant, gas flow rate is varied and measured using DC power supply unit connected to mass flow controller. All the parameters viz., solution inlet and outlet pressure, temperature and concentration, solution flow rate, gas flow rate, pressure and temperature, cooling water flow rate, inlet and outlet temperature are monitored and recorded in the computer using data acquisition unit.
During next run of experiment, by keeping solution, gas and water flow rates constant, solution initial concentration is increased by injecting R134a gas through a charging line in the weak solution tank and monitored by the online density meter. All readings are monitored and noted. This process is repeated for various solution pressures and solution initial concentrations.
In another run, the solution inlet temperature is varied by varying the cooling water temperature and keeping all other parameters constant. All readings are monitored and noted.
RESULTS AND DISCUSSION
Experimentation was conducted by varying the operating parameters viz., gas flow rate from 0.5 to 2.5 lpm, solution pressure from 120 kPa to 400 kPa, solution initial concentration from 0.01 to 0.2 kg-1 and solution temperature from 20 to 30°C. Solution flow rate and cooling water flow rate was maintained at 50 lph. Experimental results are compared with the numerical model for the bubble absorber developed earlier by Suresh and Mani (2010) to study heat and mass transfer characteristics using phenomenological theory, which was validated with the literature results. Experimental values of volumetric mass transfer coefficient, heat transfer coefficient, Sherwood number and Nusselt number are calculated using the equations given in Appendix A.
Figure 2 compares the experimental volumetric mass transfer coefficient with that of the numerical model for various gas flow rates. The agreement is good within ±14% deviation. Mass transfer coefficient increases as the gas flow rate increases due to increase in absorption rate at high gas flow rates. Figure 3 compares the experimental heat transfer coefficient with that of the numerical model for various gas flow rates. The agreement is good within ±10% deviation. Heat transfer coefficient increases as the gas flow rate increases due to increase in coupled heat transfer rate at high absorption rates.
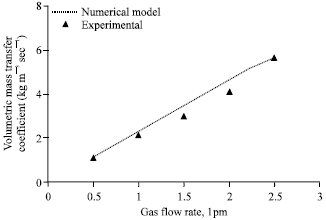 | |
| Fig. 2: | Effect of gas flow rate on volumetric mass transfer coefficient, gas inlet pressure = 650 kPa, gas inlet temperature = 32°C, solution flow rate = 50 lph, solution inelt pressure = 120 kPa, solution inlet temperature = 30°C, solution inlet concentration = 0.01 kg kg-1, Cooling water flow rate = 50 lph |
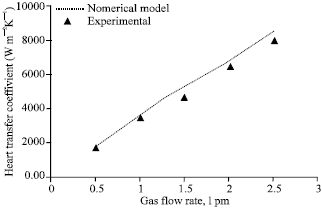 | |
| Fig. 3: | Effect of gas flow rate on heat transfer coefficient, gas inlet pressure = 650 kPa, gas inlet temperature = 32°C, solution flow rate = 50 lph, solution inlet pressure = 120 kPa, solution inlet temperature 30°C, solution inlet concentration = 0.01 kgkg-1, cooling water flow rate = 50 lph |
Figure 4 compares the experimental volumetric mass transfer coefficient with that of the numerical model for various solution pressures. The agreement is good within ±15% deviation. Mass transfer coefficient decreases as the solution pressure increases. The reason is that though the absorption rate is almost constant with respect to increase in solution pressure, the Log Mean Concentration Difference (LMCD) increases as solution pressure increases resulting in lower mass transfer coefficients.
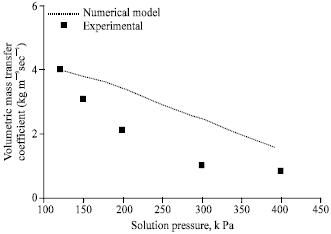 | |
| Fig. 4: | Effect of solution pressure on volumetric mass transfer coefficient , gas flow rate = 2 lpm, gas inlet pressure = 650 kPa, gas inlet temperature = 32°C, solution flow rate = 50 lph, solution inlet temperature = 0.01 kg kg-1, cooling water flow rate = 50 lph |
 | |
| Fig. 5: | Effect of solution pressure on heat transfer coefficient, gas flow rate = 2 lpm, gas inlet pressure = 650 kPa, gas inlet temperature = 32°C, solution flow rate = 50 lph, solution inlet temperature = 30 °C, solution inlet concentration = 0.01 kg kg-1, cooling water flow rate = 50 lph |
Figure 5 compares the experimental heat transfer coefficient with that of the numerical model for various solution pressures. The agreement is good within ±10% deviation. Heat transfer coefficient decreases as the solution pressure increases. The reason is that though the heat transfer rate is almost constant with respect to increase in solution pressure, the Log Mean Temperature Difference (LMTD) increases as solution pressure increases resulting in lower heat transfer coefficients.
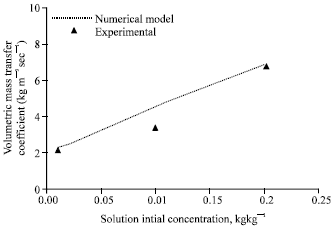 | |
| Fig. 6: | Effect of solution initial concentration on volumetric mass transfer coefficient, gas flow rate = 2 lpm, gas inlet pressure = 650 kPa, gas inlet temperature = 32°C, solution flow rate = 50 lph, solution inlet pressure = 120 kPa, solution inlet temperature = 30°C, cooling water flow rate = 50 lph |
 | |
| Fig. 7: | Effect of solution initial concentration on heat transfer coefficient, gas flow rate = 2 lpm, gas inlet pressure = 650 kPa, gas inlet temperature = 32°C, solution flow rate = 50 lph, solution inlet pressure = 120 kPa, solution inlet temperature = 30°C, coolingwater flow rate = 50 lph |
Figure 6 compares the experimental volumetric mass transfer coefficient with that of the numerical model for various solution initial concentrations. The agreement is good within ±10% deviation. Mass transfer coefficient increases as the solution initial concentration increases. Though the absorption rate is almost constant with respect to increase in solution initial concentration, the LMCD decreases as solution inlet concentration increases resulting in higher mass transfer coefficients.
Figure 7 compares the experimental heat transfer coefficient with that of the numerical model for various solution initial concentrations.
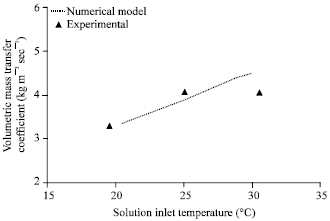 | |
| Fig. 8: | Effect of solution inlet temperature on volumetric mass transfer coefficient, gas flow rate = 2 lpm, gas inlet pressure = 650 kPa, gas inlet temperature = 32°C, solution flow rate = 50 lph, solution inlet pressure = 120 kPa, solution inlet concentration = 0.01 kg kg-1, coolingwater flow rate = 50 lph |
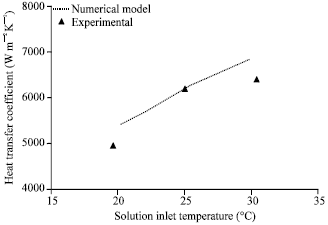 | |
| Fig. 9: | Effect of solution inlet temperature on heat transfer coefficient, gas flow rate = 2 lpm, gas inlet pressure = 650 kPa, gas inlet temperature = 32°C, solution flow rate = 50 lph, solution inlet pressure = 120 kPa, solution inlet concentration = 0.01 kgkg-1, coolingwater flow rate = 50 lph |
The agreement is good within ±10% deviation. Heat transfer coefficient increases as the solution initial concentration increases. Though the heat transfer rate is almost constant with respect to increase in solution initial concentration, the LMTD decreases as solution inlet concentration increases resulting in higher heat transfer coefficients.
Figure 8 compares the experimental volumetric mass transfer coefficient with that of the numerical model for various solution inlet temperatures. The agreement is good within ±10% deviation. Mass transfer coefficient increases as the solution inlet temperature increases.
 | |
| Fig. 10: | Variation of Sherwood number based on experiments with Sherwood number based on numerical correlation |
 | |
| Fig. 11: | Variation of Nusselt number based on experiments with Nusselt number based on numerical correlation |
Though the absorption rate decreases with respect to increase in solution inlet temperature, the LMCD also decreases as the solution inlet temperature increases resulting in higher mass transfer coefficients.
Figure 9 compares the experimental heat transfer coefficient with that of the numerical model for various solution inlet temperatures. The agreement is good within±7% deviation. Heat transfer coefficient increases as the solution inlet temperature increases. Though the heat transfer rate decreases with respect to increase in solution inlet temperature, the LMTD also decreases as the solution inlet temperature increases resulting in higher heat transfer coefficients.
Experimental values of Sherwood number and Nusselt number are evaluated and plotted against those obtained from the following correlations developed by the authors from their numerical model (Suresh and Mani, 2010).
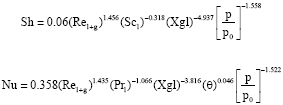 |
Figure 10 illustrates the comparison between experimental and predicted Sherwood numbers and Fig. 11 illustrates the comparison between experimental and predicted Nusselt numbers.
The agreement is fair within ±25% deviation. The deviation could be due to the combined effect of assumptions made in the theoretical model and also the inaccuracies in the measurements.
CONCLUSIONS
Experimental investigations have been carried out on a glass bubble absorber to study heat and mass transfer characteristics of R134a in Dimethyl Formamide (DMF) and the effect of parameters viz., gas flow rate, solution initial concentration, solution pressure and solution temperature on absorber performance. Heat and mass transfer coefficients determined from the experiments are compared with the numerical model and it is found that the agreement is good. Experimental values of Sherwood number and Nusselt number are evaluated and compared with those obtained from the correlations developed by the authors from their numerical model.
The following conclusions are drawn from the present study.
| • | Volumetric mass transfer coefficient and heat transfer coefficient determined from the experiments are compared with the numerical model for various gas flow rates, solution pressures, solution initial concentrations and solution inlet temperatures and the agreement is generally good with maximum deviation of ±15% |
| • | Volumetric mass transfer coefficient and heat transfer coefficients increase as the gas flow rate, solution initial concentration and solution inlet temperature increase |
| • | Volumetric mass transfer coefficient and heat transfer coefficient decrease as the solution pressure increases |
| • | Experimental values of Sherwood number and Nusselt number are evaluated and plotted against those obtained from the correlations developed by the authors from their numerical model. The agreement is generally fair within ±25% deviation |
NOTATIONS
Units, abbreviations and symbols
| A | = | Absorber cross-section area ( m-2) |
| Cp | = | Specific heat capacity (kJ kg1K-1) |
| D | = | Absorber diameter (m) |
| Dc | = | Diffusion coefficient (m-2 sec-1) |
| h | = | Heat transfer coefficient (W m-2K-1) |
| K | = | Thermal conductivity (W m-1K-1) |
| L | = | Absorber length (m) |
| M | = | Volumetric mass transfer coefficient (kg m-3 sec-1) |
| m | = | Mass flow rate (kg sec-1) |
| NU | = | Nusselt number |
| Pr | = | Prandtl number |
| p | = | Solution pressure (bar) (kPa) |
| p0 | = | Atmospheric pressure (bar) (kPa) |
| Q | = | Heat transfer rate (W) (kW) |
| Re | = | Reynolds number |
| Sc | = | Schmidt number |
| Sh | = | Sherwood number |
| X | = | Liquid mass fraction (kg kg-1) |
| T | = | Solution temperature (K) |
| U | = | Overall heat transfer coefficient (Wm -2K-1) |
| V | = | Volumetric flow rate (m-3 sec-1) |
Subscripts
| 1 | = | Inner |
| 2 | = | Outer |
| eq | = | Equilibrium |
| g | = | Gas |
| 1 | = | Liquid |
| in | = | Inlet |
| out | = | Outlet |
| v | = | Volumetric |
| w | = | Water |
| ws | = | Weak solution |
Greek symbols
| μ | = | Dynamic viscosity (Pa-s) |
| γ | = | Kinematic viscosity (m-2s-1) |
| ρ | = | Density, kgm-3 |
| α | = | Thermal diffusivity, m2sec-1 |
| θ | = | non-dimensional temperature |
APPENDIX-A
| (1) |
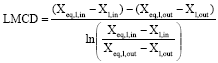 | (2) |
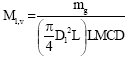 | (3) |
| (4) |
 | (5) |
| (6) |
 | (7) |
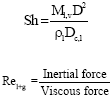 | (8) |
| (9) |
| (10) |
| (11) |
 | (12) |
| (13) |
| (14) |
θ = non-dimensional solution temperature =
| (15) |
REFERENCES
- Fatouh, M. and S.S. Murthy, 1995. Performance of a HCFC22 based vapour absorption refrigeration system. Int. J. Refrigeration, 18: 465-476.
CrossRef - Fatouh, M. and S.S. Murthy, 1996. HCFC22-based vapour absorption refrigeration system. Part I. parametric studies. Int. J. Energy Res., 20: 297-312.
CrossRef - Fatouh, M. and S.S. Murthy, 1996. HCFC22-based vapour absorption refrigeration system. Part II. Influence of component effectiveness. Int. J. Energy Res., 20: 371-384.
Direct Link - Fatouh, M. and S.S. Murthy, 1996. HCFC22-based vapour absorption refrigeration system. Part III. Effects of different absorber and condenser temperatures. Int. J. Energy Res., 20: 483-494.
CrossRef - Yokozeki, A., 2005. Theoretical performances of various refrigerant-absorbent pairs in a vapour absorption refrigeration cycle by the use of equation of state. Applied Energy, 80: 383-399.
CrossRef - Kang, Y.T., A. Akisawa and T. Kashiwagi, 2000. Analytical investigation of two different absorption modes: Falling film and Bubble types. Int. J. Refrigeration, 23: 430-443.
CrossRef - Elperin, T. and A. Fominykh, 2003. Four stages of the simultaneous mass and heat transfer during bubble formation and rise in a bubbly absorber. Chem. Eng. Sci., 58: 3555-3564.
CrossRef - Lee, J.C., K.B. Lee, B.H. Chun, C.H. Lee, J.J. Ha and S.H. Kim, 2003. A study on numerical simulations and experiments for mass transfer in bubble mode absorber of ammonia and water. Int. J. Refrigeration, 26: 551-558.
CrossRef - Merrill, T.L. and H. Perez-Blanco, 1997. Combined heat and mass transfer during bubble absorption in binary solutions. Int. J. Heat Mass Transfer, 40: 589-603.
CrossRef - Sujatha, K.S., A. Mani and S.S. Murthy, 1997. Finite element analysis of a bubble absorber. Int. J. Numerical Methods Heat Fluid Flow, 7: 737-750.
CrossRef - Sujatha, K.S., A. Mani and S.S. Murthy, 1997. Analysis of a bubble absorber working with R22 and five organic absorbents. Heat Mass Transfer, 32: 255-259.
CrossRef - Sujatha, K.S., A. Mani and S.S. Murthy, 1999. Experiments on a bubble absorber. Int. Commun. Heat Mass Transfer, 26: 975-984.
CrossRef - Staicovici, M.D., 2000. A phenemenological theory of polycomponent interactions in non-ideal mixtures. Application to NH3/H2O and other working pairs. Int. J. Refrigeration, 23: 153-167.
CrossRef - Staicovici, M.D., 2000. A non-equilibrium phenomenological theory of the mass and heat transfer in physical and chemical interactions. Part I-Theory and its application to NH3/H2O and other working systems. Int. J. Heat Mass Transfer, 43: 4153-4173.
Direct Link - Staicovici, M.D., 2000. A non-equilibrium phenomenological theory of the mass and heat transfer in physical and chemical interactions. Part II-Modeling of the NH3/H2O bubble absorption, analytical study of absorption and experiments. Int. J. Heat Mass Transfer, 43: 4175-4188.
Direct Link - Suresh, M. and A. Mani, 2010. Heat and mass transfer studies on R134a bubble absorber in R134a/DMF solution based on phenomenological theory. Int. J. Heat Mass Transfer, 53: 2813-2825.
CrossRef - Kang, Y.T., T. Nagano and T. Kashiwagi, 2002. Mass transfer correlation of NH3-H2O bubble absorption. Int. J. Refrigeration, 25: 878-886.
CrossRef - Kang, Y.T., T. Nagano and T. Kashiwagi, 2002. Visualization of bubble behavior and bubble diameter correlation for NH3-H2O bubble absorption. Int. J. Refrigeration, 25: 127-135.
CrossRef - Cerezo, J., M. Bourouis, M. Valles, A. Coronas and R. Best, 2009. Experimental study of an ammonia�water bubble absorber using a plate heat exchanger for absorption refrigeration machines. Applied Thermal Eng., 29: 1005-1011.
CrossRef








