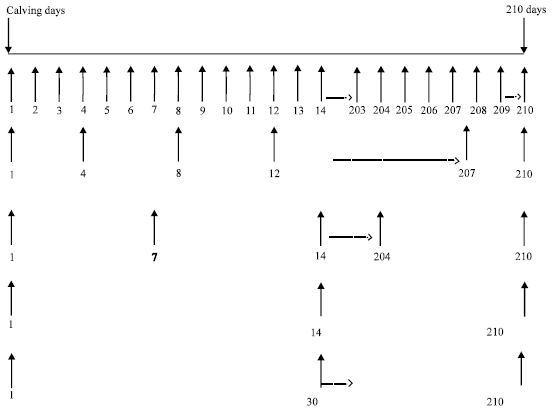
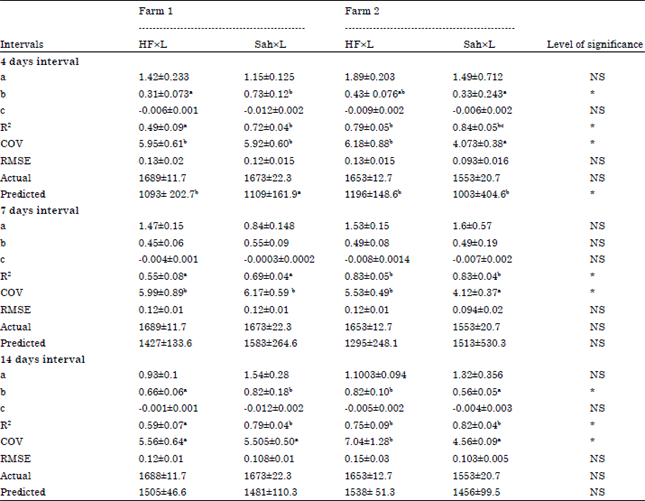
Research Article
Identification of the Suitable Milk Recording Protocol for Small-scale Dairy Production
Department of Genetics and Animal Breeding, Chittagong Veterinary and Animal Sciences University, Khulshi, Chittagong, 4225, Bangladesh
M.K.I. Khan
Department of Genetics and Animal Breeding, Chittagong Veterinary and Animal Sciences University, Khulshi, Chittagong, 4225, Bangladesh