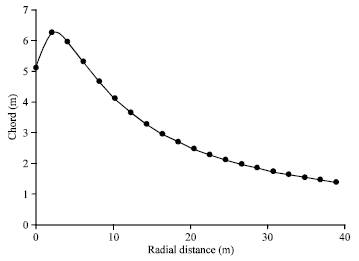
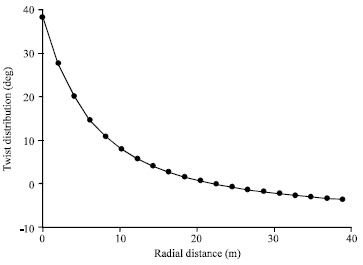
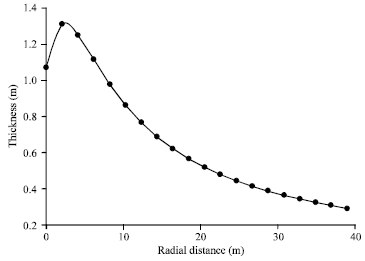
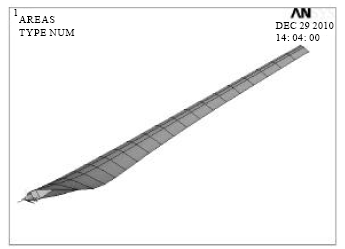
Research Article
Modal Analysis for Blade of Horizontal Axis Wind Turbine
Department of Applied Mechanics,
N.D. Mittal
Department of Applied Mechanics,
Siraj Ahmed
Department of Mechanical Engineering, Maulana Azad National Institute of Technology, Bhopal, India