Research Article
Effect of Camber Airfoil on Self Starting of Vertical Axis Wind Turbine
Department of Manufacturing and Automation, Harbin Institute of Technology, Harbin, 150001, China
Yingxue Yao
Department of Manufacturing and Automation, Harbin Institute of Technology, Harbin, 150001, China












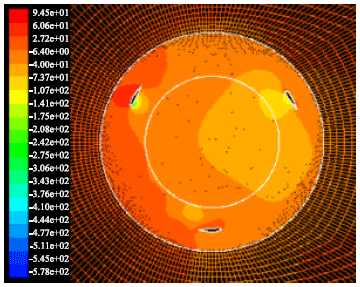
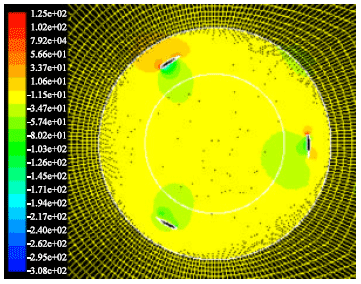

naseem salim alomoush Reply
i need best airfoil profile for vawt (H-darrieus) to get 100W ,at 5m/s design speed.
Habtamu B.T
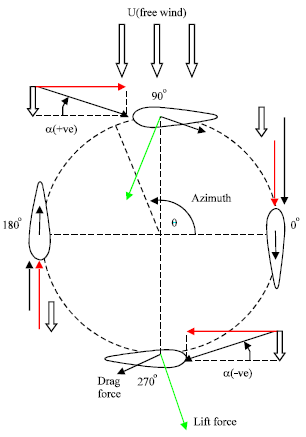
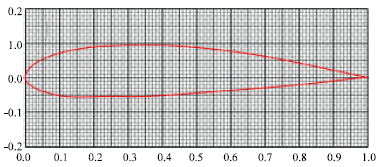
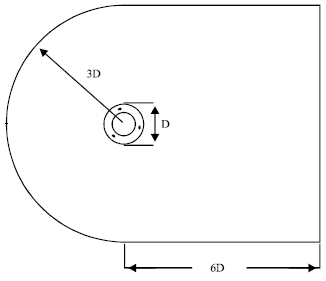
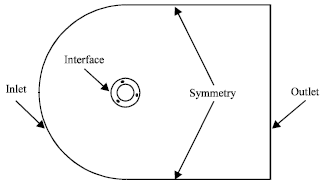
The main draw backs with VAWT is self starting at low reynold numbers. the most commonly used airfoil profiles are NACA0012,NACA0015, and NACA0018. however, these profiles have self starting problems. airfoils with self staring airfoils like camber airfoil have efficency problems. therefore, there is no best airfoil profile I recommend.