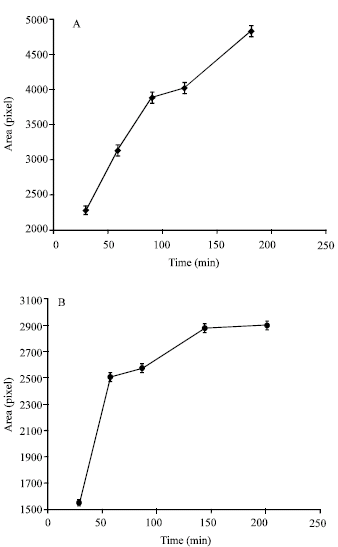
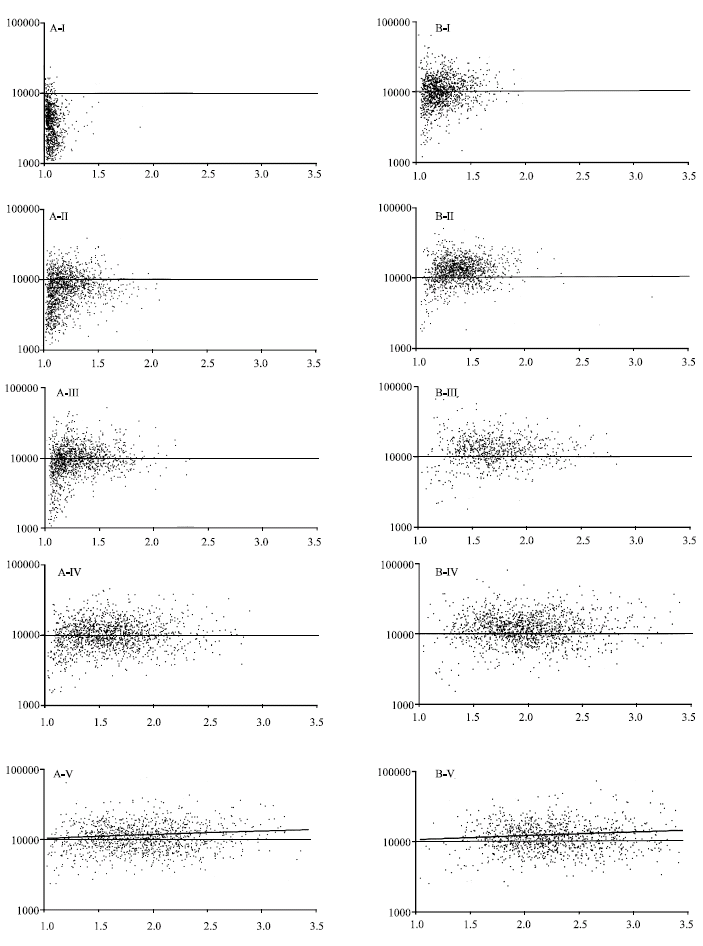
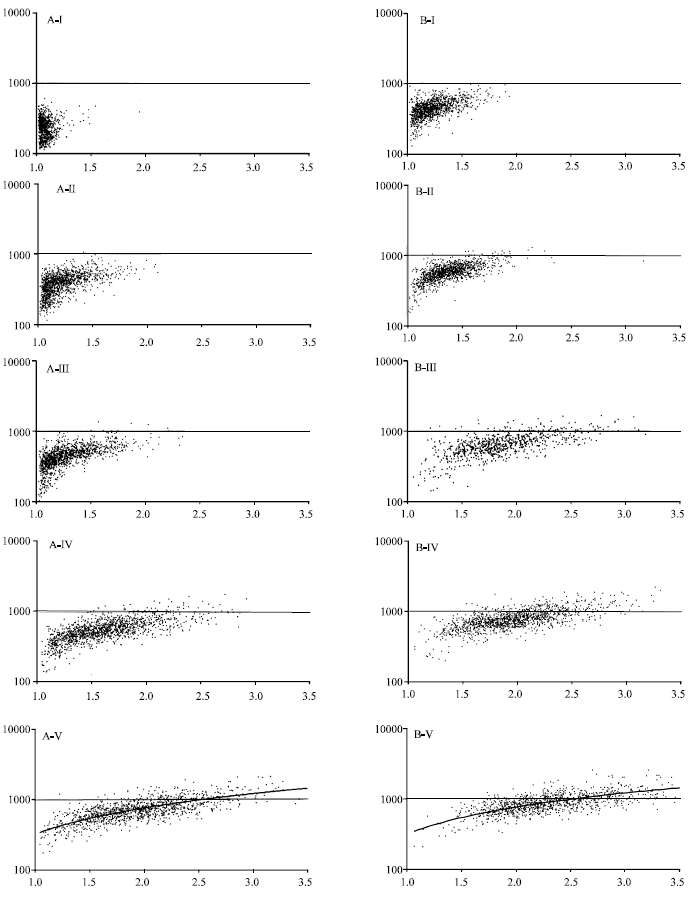
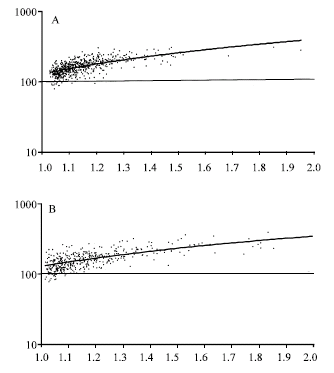
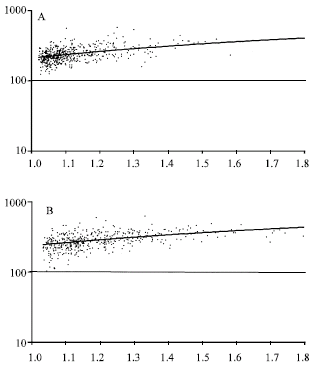
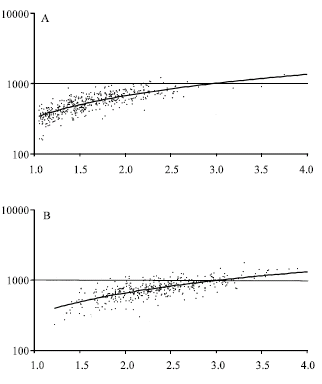
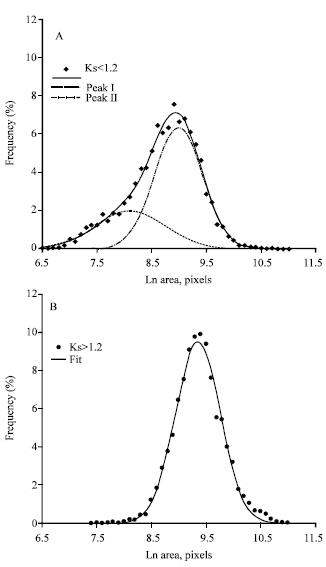
Research Article
Spreading as a General Attribute of Cell Population
Department of Cell Culture, Institute of Cytology, Russian Academy of Sciences, St. Petersburg, Russia
T.A. Krylova
Department of Cell Culture, Institute of Cytology, Russian Academy of Sciences, St. Petersburg, Russia
N.V. Tsupkina
Department of Cell Culture, Institute of Cytology, Russian Academy of Sciences, St. Petersburg, Russia
V.P. Pershina
Department of Cell Culture, Institute of Cytology, Russian Academy of Sciences, St. Petersburg, Russia