ABSTRACT
In this study, we first briefly introduce the development status of core cryptographic primitives related to implementation of receipt-freeness and coercion-resistance. These core cryptographic primitives consist of blind signature, deniable encryption, mix net/verifiable shuffles, designated verifier proof/signature, knowledge proof protocol, plaintext equivalence test, secure multi-party computation and deniable authentication protocol. Then, a typical deniable encryption scheme is analyzed and improved. Moreover, the state-of-art of receipt-freeness and coercion-resistance, based on the internet voting model proposed by us, is presented. Finally, the status in quo of formal analysis of receipt-freeness and coercion-resistance is discussed.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/itj.2009.934.964
URL: https://scialert.net/abstract/?doi=itj.2009.934.964
INTRODUCTION
With the development of internet technology, many transactions are carried out through the internet. With the help of the internet voting system people can use the internet to express his opinion in the elections. Compared with other voting methods, Internet voting has several advantages. For example, internet voting may make it easier for voters to join in elections; internet voting also can lower the cost of voting for the entire election and it has the potential abilities to eliminate problems such as vote buying and coercion on voter. Internet voting protocol is the base of the internet voting system.
The practical secure internet voting protocol should have the following properties:
Basic properties: Privacy, completeness, soundness, unreusability, fairness, eligibility and invariableness.
Expanded properties: Universal verifiability, receipt-freeness, coercion-resistance.
| • | Universal verifiability (Sako and Kilian, 1995): Any one can verify the fact that the election is fair and the published tally is correctly computed from the ballots that were correctly cast |
| • | Receipt-freeness (Benaloh and Tuinstra, 1994): The voter can not produce a receipt to prove that he votes a special ballot. Its purpose is to protect against vote buying |
| • | Coercion-resistance (Juels and Jakobsson, 2002): A coercion-resistant voting protocol should offer not only receipt-freeness but also defense against randomization, forced-abstention and simulation attacks |
In elections the briber may bribe the voter to cast a vote for a special candidate and the coercive adversary may force the voter to vote a special ballot to break the fairness of the elections. Hence, receipt-freeness and coercion-resistance play an important role in the elections. So, how to develop an efficient secure internet voting protocol with receipt-freeness and coercion-resistance is very important. In the last 15 years, many experts have used different technologies to develop the internet voting protocol with receipt-freeness and coercion-resistance.
Until today several serveys (Nurmi and Salomaa, 1998; Burmester and Magkos, 2002; Bungale and Sridhar, 2003; Mason, 2004; Goulet and Zitelli, 2004; Karlof et al., 2005; Smith, 2005b; Sampigethaya and Poovendran, 2006; Cetinkaya and Cetinkaya, 2007; Hill, 2008) discuss the electronic voting protocol/system. Owning to the rapid development of receipt-freeness and emergence date of coercion-resistance these above surveys do not seriously concern the state-of-art of receipt-freeness and coercion-resistance. Motivated by this, we survey the state-of-art of receipt-freeness and coercion-resistance. The survey processes in three different lines: The first line follows the trace of emergence and developments of receipt-freeness and coercion-resistance, the second line is to analyze the features when concrete technologies are used during development and the third line is to discuss what formal methods are used and how to analyze these secure properties during developments.
The main contributions of this study are summarized as follows:
| • | The state-of-art of receipt-freeness and coercion-resistance is presented |
| • | The status in quo of the core technologies related to develop receipt-freeness and coercion-resistance is introduced |
| • | The development status of formal analysis of receipt-freeness and coercion-resistance is discussed |
| • | The deniable encryption scheme (Klonowski et al., 2008) is analyzed and improved |
| • | An internet voting model is proposed |
To present knowledge, there are several reviews which discuss the developments of electronic voting protocol/system. Nurmi and Salomaa (1998) compared and discussed six secret balloting schemes with respect to criteria related to the possibility of voters to check that their votes have been correctly assigned, to the vulnerability of the protocols to electoral fraud of various sorts and to the vulnerability of protocols to vote selling. Burmester and Magkos (2002) overview mix-net, blind signatures and homomorphic encryption model and assess their security and practicality. They also compare the e-voting to I-voting and give their disadvantages and advantages. Bungale and Sridhar (2003) give a short survey of the projects in electronic voting including Internet voting and electronic poll-site voting. Mason (2004) discussed some of the practical and security issues that affect remote electronic voting. Goulet and Zitelli, (2004) provided an examination of these existing protocols and identified the strengths and weaknesses of each under different election premises. Karlof et al. (2005) surveyed the cryptographic voting protocols from a systems perspective. Smith (2005b) surveyed the contributions of the entire the oretical computer science/cryptography community during 1975-2002 that impact the question of how to run verifiable elections with secret ballots. He argues that the approach based on homomorphic encryptions is the most successful. It is explained precisely what these ideas accomplish but also what they do not accomplish and a short history of election fraud throughout history is included. Sampigethaya and Poovendran (2006) survey the requirement from the general security, adversary counter-attack and system implementation. Based on how voters submit votes to tallying authority, they propose the classification for voting schemes: hidden voter, hidden vote and hidden voter with hidden vote. They also discuss each class in detail and analyze some existing schemes under their framework. Cetinkaya and Cetinkaya, 2007 described some verification and validation activities and explains the relationship between verification and validation and core requirements that any e-voting system should satisfy Hill (2008) discussed the manual, combination and electronic voting systems in his report. All above surveys do not discuss deeply the status of receipt-freeness and coercion-resistance.
In this study, we first briefly introduce the development status of core cryptographic primitives related to implementation of receipt-freeness and coercion-resistance. These core cryptographic primitives consist of blind signature, deniable encryption, mix net/verifiable shuffles, designated verifier proof/signature, knowledge proof protocol, plaintext equivalence test, secure multi-party computation and deniable authentication protocol. At the same time the typical deniable encryption scheme (Klonowski et al., 2008) is analyzed and improved. Then, the state-of-art of receipt-freeness and coercion-resistance, based on the internet voting model proposed by us, is presented. After that, the status in quo of formal analysis of receipt-freeness and coercion-resistance is discussed. Finally, we conclude the study and suggest feasible future studies.
THE THEORETICAL AND PRACTICAL IMPLICATION
Voting plays an important role in democratic society. With the development of information technology and internet people can replace the traditional voting methods with a new voting method called internet voting.
Owning to the importance of receipt-freeness and coercion-resistance, in the last fifteen years a lot of great achievements related to internet voting protocol with receipt-freeness and coercion-resistance have been accomplished. The previous surveys do not seriously concern the state-of-art of receipt-freeness and coercion-resistance. Hence, it is absolutely necessary to review state-of-art of receipt-freeness and coercion- resistance.
Moreover, people can also get the status in quo of formal proof of receipt-freeness and coercion-resistance. With the above information people can know the direction of the development of internet voting protocol with receipt-freeness and coercion-resistance.
CORE CRYPTOGRAPHIC PRIMITIVES
In the study, we can find several core cryptographic ptimitives including secret sharing, threshold encryption scheme, blind signature, secret sharing, threshold public key encryption, deniable encryption, mix net/verifiable shuffles, designated verifier proof/signature, knowledge proof protocol, plaintext equivalence test, secure multi-party computation and deniable authentication protocol, are used to implement receipt-freeness and coercion-resistance. Secret sharing is a method to distribute secret into n parts and allow the m parts of shares to construct the original secret (m<n). A threshold public-key encryption scheme is used to share a secret key among n talliers such that messages can be decrypted only when a substantial subset of talliers cooperate.
Blind signature: Blind signature, introduced by Chaum (1985, 1998), allow a person to get a message signed by another party without revealing any information about the message to the other party. Suppose Alice has a message m that she wishes to have signed by Bob based on RSA public key cryptosystem and she does not want Bob to learn anything about m. Let (n, e), (n, d) be Bob's public, private key of RSA. Alice generates a random value r gcd (r, n) = 1 and sends m' = (mre) to Bob. The value m is blinded by r; hence Bob can derive no useful information from it. Bob returns the signed value s' = m'd to Alice. Since,
So, Alice can obtain the true signatures. Provably secure threshold blind signature scheme can be find in the studies (Liem, 2003; Cao et al., 2006; Wu and Chen, 2009).
Homomorphic encryption scheme: An encryption scheme is said to be homomorphic if for any given encryption key k the semantically-secure public-key encryption function E( ) satisfies: Let M denote the set of the plaintexts, C denote the set of the ciphertext.
We say a scheme is additively homomorphic if we consider addition operators and multiplicatively homomorphic if we consider multiplication operators.
RSA: We suppose that the public key is (n, e), private key is d. m1, m2 ∈ M, c1 = E (m1) = m1e mod n, c2 = E (m2) = m2e mod n, then;
So, RSA public key cryptosystem is multiplicatively homomorphic cryptosystem.
ElGamal: ElGamal is actually a homomorphic encryption whose binary operation is multiplication. The public key is the tuple (G, p g, y) where G is a group, p is the order of the group, g is a generator of that group. y = gz for some secret key z. m1, m2 ∈ M, x1, x2 are the random numbers.
So, ElGamal public key cryptosystem is multiplicatively homomorphic cryptosystem.
Paillier: Paillier cryptosystem (Paillier, 1999), named after and invented by Paillier (1999), is a probabilistic asymmetric algorithm for public key cryptography. (n, g) is public key; (p, q) remains private. m1, m2 ∈ M, x1, x2 are the random numbers. The encryption algorithm is Ex (m) = gm xn mod n2. D( )is decryption algorithm.
So, Paillier cryptosystem public key cryptosystem is addition homomorphic cryptosystem. We can also get:
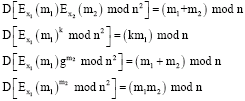 |
If m1, m2 ∈ M, r is a random number then D [Ex (m)rn mod n2] = m.
Deniable encryption: The traditional encryption is to protect the privacy of information against the attacks and unauthorized access from the passive adversary. In some scenarios the adversary accesses the cipertext and force the sender/receiver to present the key or the plaintext. For traditional encryption, the sender and receiver can not cheat and disclose an incorrect plaintext owning to the fake key would produce senseless information. Deniable encryption can be used against revealing information that the owner of the information may decrypt it in an alternative way to a different plaintext. The notion of deniable encryption was introduced by Canetti and Gennaro (1996). The sender is able to deniable encryption to encrypt a hit b in such a way that the resulting ciphertext can he interpreted as either b or 1-b to a coercer.
Canetti et al. (1997) classified deniable encryption into three schemes according to which parties may be coerced: the sender-deniable scheme, the receiver-deniable scheme and the-sender-and-receiver deniable schemes. At the same time, they also proposed a public-key deniable encryption, which includes basic and party deniable schemes and a shared-key deniable encryption, which includes a one-time-pad and plan-ahead shared-key deniable schemes.
Assange and Weinmann (1997) proposed a deniable encryption file system called Rubberhose file system which is a deniable encryption package that lets a person not wanting to disclose plaintext data corresponding to their encrypted data show that there is more than one interpretation of the latter.
Rjaiskova (2002) proposed a sender-deniable public-key deniable encryption based on RSA cryptosystem, in which the message is encrypted per bits. The sender encrypts the message using the public key of the receiver and he can later fake his random choices. The deniable encryption is very inefficient. Sending 1 bit through the deniable encryption proposed by Rja(|skov´a means sending 105 bits through the public channel. At the same time he also proposed a generalized party scheme.
Klonowski et al., (2008) expended the schemes (Canetti et al., 1997) and propose a receiver deniable encryption scheme based on the ElGamal cryptosystem and apply it to implement the covert channel. However, according to present analysis we find that the receiver deniable scheme is not receiver-deniability.
In the following part we give the analysis of deniable scheme (Klonowski et al., 2008).
The researcher assumes that the sender and the receiver share the secret key s. The sender knows the private key x ∈ {2, 3,….,ord g–1} of the receiver based on ElGamal cryptosystem. The sender has no public and private key.
| • | Encryption: To encryption a message mf and an illegal message m ∈ ⟨g⟩, k = HASH (s||mf) is computed. Then, the sender computes (α = gk• m, β = (gk • mx) • mf) which is the ciphertext of mf and sends it to the receiver |
| • | Decryption: The receiver computes β•α-x = (yk • mx) •mf (gk • m)-x = mf and gets mf. Then, the receiver computes k = HASH (s||mf) and m = β • g-k |
| • | Dishonest opening: If the receiver coerced he can reveal his private key x, the coerced can check that (α, β) is the ciphertext of mf |
Because the sender, receiver and coercer know the deniable encryption scheme the coercer can force the receiver reveals the secret key s, then the coercer can compute k = HASH (s||mf) and gets m = β • g-k. So, the coercer can know the illegal message m. According to the definition of receiver deniable encryption the receiver deniable encryption scheme proposed by Klonowski et al., 2008 is not receiver deniable encryption scheme.
In order to address the problem we can use the parity deniable encryption scheme proposed by Canetti and Gennaro (1996). Why the coercer can know the illegal message m? The reasons are that the coercer knows the deniable encryption scheme according to Kerckhoffs principle and the secret information x and s. If we do not point that which message in two messages is illegal in the deniable encryption scheme, however we decide which message is the illegal message in each run based on the choice of the sender or the receiver using the parity deniable encryption scheme. The new deniable encryption scheme is the sender-receiver deniable encryption. The parity scheme is firstly executed then the deniable encryption is run. The parity scheme tell the receiver which message is the illegal message, the first one or second, then the receiver can know which message the illegal message. If the coercer know the message mf and m, he can find which message is illegal, so the receiver can tell the coercer any one of two message mf and m is illegal, thus make the deniable encryption have receiver deniable encryption. Owning to the parity deniable encryption scheme the encryption is the receiver deniable encryption.
Ibrahim (2009a) devises a sender-deniable public-key encryption based on quadratic residuosity of a composite modulus and showed how to device a sender-deniable public-key encryption from any trapdoor permutation. His scheme is impractical. In later study, Ibrahim (2009b) also proposes a receiver-deniable public-key encryption scheme based on mediated RSA PKI and oblivious transfer protocol. But deniability in the scheme is worth discussing.
![]() (2002) uses deniable encryption to implement the untappable channel which is used in the electronic voting protocol. Canetti and Gennaro (1996) apply the public-key, sender-deniable encryption scheme to propose a secure multiparty computation which permit a set of parties to compute a common function of their inputs while keeping their internal data private even in the presence of a coercer and can be used to provide the receipt-freeness of electronic voting protocol.
(2002) uses deniable encryption to implement the untappable channel which is used in the electronic voting protocol. Canetti and Gennaro (1996) apply the public-key, sender-deniable encryption scheme to propose a secure multiparty computation which permit a set of parties to compute a common function of their inputs while keeping their internal data private even in the presence of a coercer and can be used to provide the receipt-freeness of electronic voting protocol.
Mix net/verifiable shuffles: Anonymity is an aspect of privacy in the security field. Anonymity means that people may use a resource or service without disclosing his identity. Tatli et al. (2006) point out that anonymity should fall into two categories: communication anonymity and content anonymity. Generally, people mainly concern the communication anonymity. They also argue that there are three methods to implement the communication anonymity: proxies, Peer-to-Peer (P2P) networks and mix-net (Chaum, 1981).
In a proxy-based method, a proxy that the sender and the receiver must trust it receives the message from the sender and, changes some parts of the message in order to hide sender‘s identity information and sends it to the receiver. When get the message from the receiver the proxy in turn forward it to the real sender. Generally, there are two shortages in the proxy-based method. The first one is that users have to trust the proxy unconditionally. The second is that there are no protection mechanisms in the channel between users and proxies.
In the P2P networks the user chooses a random path and sends the message along this path to the final receiver. Unlike anonymizer, there is no need for a trusted party within these systems.
The last method, mix-net, is a more promising approach for the Internet voting system compared to proxies and P2P networks. A mix-net consists of a series of entities, called mix server, each of which has a public key. Each mix server receives encrypted messages and then decrypted, batched, their order permuted and forwarded on after stripping the sender’s identifying information.
A secure mix-net should have: correctness, privacy, robustness and efficiency. Correctness means that the result is correct if all mix-servers are honest. Privacy implies that if a fixed minimum number of mix-servers are honest privacy of the sender of a message is ensured. Robustness implies that if a fixed number of mix-servers are honest, then any attempt to cheat is detected and defeated. Efficiency means that the study done by a verifier is independent of the number of mix servers. The computational work done by each server is independent of the number of servers except some negligible ones like addition. Universal Verifiability means that correctness of the result is verifiable for any verifiers.
The first RSA-based Mix-net was introduced by Chaum (1981) for anonymous e-mail communication. Chaum argues and proves that the mix-net can protect against a passive adversary who can eavesdrop on all communications between mix servers but is unable to observe the permutation inside each mix. But Chaum’mix-net is individual verifiability. Pfitzmann and Pfitzmann (1990), however, show an active attack by a sender, which is more complicated than a simple repeated ciphertext attack. Mitomo and Kurosawa (2000) point that there is one problem the size of each ciphertext is very long proportionally to the number of mix servers owning to the use of RSA cryptosystem in Chaum’s mix net. Park et al. (1994) overcome this problem by using ElGamal encryption scheme so that the size of each ciphertext became independent of the number of mix servers.
Sako and Kilian (1995) firstly propose a universally verifiable mix net with zero knowledge proof. The ideal of their mix-net is that each mix server must prove that he behaved correctly with zero knowledge proof. Ogata et al. (1997) showed the first robust mix net which is also universally verifiable. Mitomo and Kurosawa (2000) point that the computational cost of each mix server is O(κtN) and the external verifier’s cost is also O(κtN), where κ is the securityp arameter and t denotes the number of malicious mix servers.
Abe (1998) showed a new robust mix net in which the external verifier’s cost is reduced to O(κN). At the same time, Jakobsson (1998) showed a more efficient robust mix net, called practical MIX, but which is not universally verifiable. He does not use cut and choose methods, use repetition robustness. Desmedt and Kurosawa (2000) had broken the mix-net in 2000.
Jakobsson (1999) proposed his second robust mix net, called flash mixing. This scheme is the most efficient robust mix net known so far which satisfies v = O(t) and can against the attack (Desmedt and Kurosawa, 2000). Mitom and Kurosawa (2000) break the mix net (Jakobsson, 1999) with a viant of the attack (Desmedt and Kurosawa, 2000) and give a countermeasure for this attack. Li et al. (2007) analyze the scheme (Gao et al., 2003) and find that it does not satisfy ![]() resilience.
resilience.
Pfitzmann (1995) has given some general attacks on mix-nets and Michels and Horster (1996) give additional attacks. Wikstrom (2004b) gives several attacks for a protocol Golle et al. (2002). Abe and Imai (2003) have independently find related attacks on schemes (Jakobsson and Juels, 2001; Golle et al., 2002) and give a formal definition of anonymity and robustness of mix net, but they do not propose a mix net which satisfy these requirements of security.
Wikstrom (2004a) gives the first definition of a universally composable mix-net and also the first construction with a complete security proof.
An important tool in the construction of a mix-net is a so called proof of shuffle. By making each mix server performs a verifiable shuffle observers can become confident that each mix server really is working as advertised. If several mutually distrustful parties consecutively perform verifiable shuffles to n items, then the resulting permutation is unknown to anybody.
A verifiable shuffle is an algorithm that is given n encrypted messages as input. It then shuffles those messages, i.e., permutes them into an apparently random order, while at the same time replacing each encrypted message by a re-encryption of that message. Finally, the shuffled and reencryted messages are output.
The first efficient methods to achieve this were given independently by Neff (2001) and Furukawa and Sako (2001), respectively. Groth (2003) generalizes Neff’s approach and improve its efficiency. Subsequently, other authors improve and complement these methods (Furukawa, 2005; Wikstrom and Groth, 2006).
A different approach was given by Wikstrom (2005). Wikstrom (2005) introduced the first El-Gamal based mix-net in which each mix-server partially decrypts and permutes its input, called sender verifiability, i.e., no reencryption is necessary. He proves the security of the mix-net in the UC-framework against static adversaries corrupting any minority of the mix-servers. At the same time he constructs the first proof of a decryption-permutation shuffle and show how this can be transformed into a zero-knowledge proof of knowledge in the UC-framework.
Recently Adida and Wikstrom (2007) construct public-key obfuscations of a decryption shuffle based on the Boneh-Goh-Nissim cryptosystem and a re-encryption shuffle based on the Paillier cryptosystem. Both allow efficient distributed verifiable decryption. But the performance of their mix-net is much worse than that of known constructions.
Designated verifier proof/signature: In traditional digital signature we use it to authenticate the identity of message of the sender without the sender’s cooperation. But in some special Internet based applications, such as Internet voting, electronic biding, electronic business, when authenticate the identity of the sender we require the signer cooperation. This special digitial signature is called undeniable signature (Chaum and Van Antwerpen, 1990). The idea of this type of interactive signatures was similar to the idea of one time signature (Merkle, 1978). Deniable signature not only has the traditional digitial signature function but also has the additional function that it can not be verifed without the cooperation of the signer. The true signer can use a confirmation protocol to prove his identity of the signer to a verifier. The fake signer can use a denial protocol to deny his digitial signature to a verifier. In other words, only the true signer can successfully complete a confirmation protocol and not able to successfully complete a denial protocol for any of his signatures. Therefore, the true signer can not deny having produced his signatures. Desmedt and Yung (1991) point out that in the scheme (Chaum and van Antwerpen, 1990), the signer does not assure that to whom he is proving the validity of a signature. Jakobsson (1994) finds that the undeniable signature scheme (Chaum and van Antwerpen, 1990) is not security to a blackmailing attack. Deniable signature places significant inconvenience and workload on verifiers and conformers, compared to an off-line non-interactive verification.
To address the problem, Jakobsson et al. (1996) propose Designated-Verifier Proof/Signature (DVP/S). Independently Chaum (1996) proposes the notion of private signatures in the patent. A DVP/S is a proof of correctness of some statement that either the prover or some designated verifier could have generated. If prover creates the proof, the statement is correct. At the same time a designated verifier could simulate a valid proof without a correct statement. A secure DVP/S should convince the designated verifier of the correctness of the statement since the designated verifier knows that he did not create the proof himself. But no other party will be convinced of the validity of the proof since the designated verifier could have created it. In other words In a DVP/S scheme, the signature authenticate a message, but without providing a non-repudiation property of traditional signatures. The DVP/S scheme (Jakobsson et al., 1996) is the first non-interactive undeniable signature scheme that transforms the scheme (Chaum, 1990) into a non-interactive verification using a designated verifier proof. Wang (2003) points that DVP/S scheme (Jakobsson et al., 1996) is insecure by demonstrating a simple attack that allows a dishonest signer to convince a designated verifier receiving invalid signatures and gives two intuitive countermeasures against this attack.
Following this idea, Galbraith and Mao (2003) propose a non-interactive undeniable signature scheme based on RSA in the multi-user setting to have anonymity and invisibility. Libert and Quisquater (2004) proposed an identity-based undeniable signature scheme that can be regarded as the identity-based version of Galbraith-Mao’s scheme using pairings. Bender et al. (2006, 2009) described 2-user ring signatures that immediately give rise to designated verifier signatures in the standard model.
In 2003, Steinfeld et al. (2003) proposed a new notion called Universal Designated Verifier Signatures (UDVS) which is a useful property for traditional signatures. The essence of the UDVS is a transformation from a publicly verifiable signature to a designated verifier signature, which is performed by the signature holder who does not have access to the signer's secret key. In other words, a UDVS scheme can function as a standard publicly-verifiable digital signature but has additional functionality which allows any holder of a signature (not necessarily the signer) to designate the signature to any desired designate diversifier (using the verifier’s public key). Given the designated signature, the designated verifier can verify that the message was signed by the signer, but is unable to convince anyone else of this fact. They propose an efficient deterministic UDVS scheme constructed using any bilinear group-pair. Steinfeld et al. (2004) proposed a UDVS based on Schnorr and RSA signatures. Laguillaumie et al. (2006) proposed two fairly efficient UDVS schemes which are unforgeability and anonymity in the standard model and do not need the KEA assumption. Zhang et al. (2005) proposed a Short signature and UDVS scheme based on the bilinear pairings whose security can be analyzed without the random oracle assumption.
Baek et al. (2005) pointed out that one inconvenience of all the previous UDVS schemes is that they require the designated verifier to create a public key using the signer's public key parameter and have it certifed to ensure the resulting public key is compatible with the setting that the signer provided. This restriction is unrealistic in several situations where the verifier is not willing to go through such setup process. They use an alternate method to realize UDVS (Steinfeld et al., 2003), called universal designated verifier signature proof based on the pairing-based signature schemes.
A designated verifier signature scheme is useful in some situations in which the signer should specify who may be convinced by the signer's signature. However, in some circumstances, the third party may be convinced with high probability that the signature intended for the designated verifier is actually generated by the signer. For example, the signature may be captured on the line by the third party before the designated verifier receives it. The third party can then confirm that the real signer is Alice. To protect the identity of the signer in such situations, the signer encrypts the signature with the designated verifier’s public key so that only the designated verifier can get the signature generated by the signer with his secret key. This stronger requirement is called a strong designated verifier signature scheme and was discussed in the study (Jakobsson et al., 1996). Saeednia et al. (2004) proposed a new efficient designated verifier signature scheme based on a combination of the Schnorr signature and Zheng signcryption schemes, which directly provides the strongness property without requiring any encryption of the signatures. In their scheme, the third party cannot even verify the signature since the secret key of the designated verifier is involved in the verification step. If the secret key of the designated verifier is exposed to the public, then anyone can verify the signature. However, still no one can confirm that the signature is from the signer or the designated verifier. Susilo et al. (2004) proposed an identity-based SDVS scheme based on pairings. But, Kancharla et al. (2007) pointed out that SDVS scheme of Susilo et al. (2004) is vulnerable to non deligatability. Non delegatability of a DVS means that a valid designated-verifier signature constitutes a proof of knowledge of either prover’s or designate verifier’s secret key. They propose an Identity Based Strong Designated Verifier Signature (IBSDVS) scheme using bilinear pairings and prove that their scheme is secure against existential forgery under adaptively chosen message and identity attack in random oracle model.
Laguillaumie and Vergnaud (2005) formalized the notion of privacy of signer’s identity which captures the strong designated verifier property and designed an efficient construction for strong DVS based on any bilinear map.
Lee and Chang (2006) proposed a strong designated verifier proof signature without hash functions and prove that their scheme provides signer anonymity, unforgeability and the strong designated verifier property. Huang et al. (2008) proposed the first construction of short strong designated verifier signature scheme. Their scheme is very efficient in terms of signature generation and the signature length. In particular, the signature length of our scheme is only log2 (q), which is the shortest compared to the existing schemes. At the same time they also extend our scheme to construct a short identity-based strong designated verifier signature scheme.
Cramer et al. (1994) proposed a new scheme for achieving 1-out-of n group signature that allows a signer to produce a signature in the name of an ad-hoc decided group of people, without requiring the interaction of the others. Later Rivest et al. (2001) formalized this kind of signature called ring signatures. They also showed how to achieve a designated verifier signature scheme where two participants in a ring signature collaborate and generate a signature. Huang et al. (2008) point out that should note that the construction does not satisfy the strongness property of SDVS scheme, since the secret key of the verifier is not required to verify the authenticity of the signature. Following this idea, multi-designated verifier signature scheme was proposed in the study (Laguillaumie and Vergnaud, 2004). Ring signatures, when restricted to two users, can also be viewed as designated-verifier signatures, where one user is the actual signer and the other user is the designated-verifier who can also forge the two-user ring signature, thus providing signer anonymity in the context of ring signatures. Boneh et al. (2003) proposed a ring signature based on bilinear group-pairs and observed that it also allows public conversion of single-signer ring signatures into two-signer ring signatures. Thus, the ring signature scheme (Boneh et al., 2003) can also be viewed as a UDVS scheme. Wang et al. (2007) survey the state-of-the-art of ring signature.
Chameleon signatures (Krawczyk and Rabin, 2000) allow designation of signatures to verifiers by the signer and in addition allow a signer to prove a forgery by a designated verifier. Chameleon signatures that provide with an undeniable commitment of the signer to the contents of the signed document as regular digital signatures do but at the same time do not allow the recipient of the signature to disclose the contents of the signed information to any third party without the signer’s consent. These signatures are closely related to undeniable signatures but chameleon signatures allow for simpler and more efficient realizations than the latter. In particular they are essentially non interactive and do not involve the design and complexity of zero knowledge proofs on which traditional undeniable signatures are based Instead chameleon signatures are generated under the standard method of hashthensign. Zhang et al. (2003) construct some ID-based chameleon signature schemes based on the proposed two new ID-based Chameleon hashes from bilinear pairings. Ateniese and Medeiros (2004) proposed the first identity-based chameleon hash function based on RSA and a id-based chameleon signature and a novel sealed-bid auction scheme that is robust, communication efficient and secure under a particular trust model.
Proof protocol that two ciphertexts are encryption of the same plaintext: Research on the proof protocol that two ciphertexts are encryption of the same plaintext is at the beginning. Baudron et al. (2001) proposed an interactive proof protocol based on paillier cryptosystem. Acquisti (2004) applies the idea of Baudron et al. (2001) and proposed an interactive proof protocol based on paillier cryptosystem with the condition p = 2. Goulet and Zitelli, (2004) proposed an interactive protocol based on ElGamal cryptosystem. But we find that Goulet and Zitelli, (2004) proof protocol is wrong. In the following, we address the problem of Goulet and Zitelli, (2004) and give an improved proof protocol that two ciphertexts are encryption of the same plaintext:
In the protocol, we need two public and private keys: (p, g, hV), αV, hV = gαV: (p, g, hC), αC, hC = gαC, g is a generator of multiplicative ![]() .
.
Prover proves to the verifier that ![]() and
and ![]() are the ciphertexts of the same m with the public key (p, g, hV) and (p, g, hC). At the same time prover does not tell verifier rV, rC.
are the ciphertexts of the same m with the public key (p, g, hV) and (p, g, hC). At the same time prover does not tell verifier rV, rC.
| • | Prover computes: |
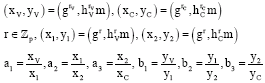 |
sends (a1,a2,a3,b1,b2,b3)to verifier
| • | Verifier checks: |
Verifier selects a random value c from c ∈ {0, 1, 2} the set and sends c to the prover.
Prover computes:
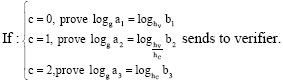 |
If we repeat the above procedure z times, we see that a lying prover only succeeds with a probability of (2/3)Z, which is a probability that shrinks quickly if we repeat enough times. Thus, the verifier can be sure with a large probability that the plaintext equivalence is true after a number of run of this proof.
Plaintext equivalence test: The notion of Plaintext Equivalence Test (PET) is proposed by Jakobsson and Juels (2000), which is cryptographic primitive that operates on ciphertexts in a threshold cryptosystem. They give a PET protocol based on ElGamal cryptosystem. The input to PET is a pair of ciphertexts; the output is a single bit indicating whether the corresponding plaintexts are equal or not.
This is achieved by dividing the two El-Gamal encryptions and verifying that the results encrypt the value 1. Thus, let (α, β) = (gr, hr, m1) and (γ, σ) = (g8, h8, m2) be the two El-Gamal ciphertexts where r and s are random; if m1 = m2, then (α/γ, β/σ) = (gr–s, hr–s 1). To complete the verification, the resulting encryption (gr–s, hr–81) must be proved to encrypt the value 1. That can be accomplished by anybody who knows the decryption key l where h = gl; or by joint decryption by mutually distrustful parties who had previously secret-shared the ElGamal decryption key. Since, 1z = 1 whereas with high probability in a group of large prime order xz ≠ 1 if xz ≠ 1 and z is random, it suffices to produce, not the decryption itself, but rather a random power of it;
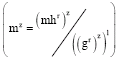 |
thus definitely revealing zero knowledge about the plaintext even if the random quantities r and s had in fact been maliciously chosen.
PET may be realized as an efficient distributed protocol that reveals no additional, non-negligible information about plaintexts. For a detailed description of efficient methods to perform this verification, along with proofs of the properties of the construction (MacKenzie et al., 2002).
Secure multi-party computation: In 1982 the Secure Multi-Party Computation (SMC) was introduced by Yao (1982a). The SMC set up a protocol that n several mutually distrustful parties to compute an agreed function of their inputs in a way guaranteeing the correctness of the output. We suppose that the inputs of party i is xi = (i = ,..,n), we want to compute function (xi,….xn) such that party i is guaranteed to learn yi, but can get nothing more than that. If all outputs are the same we often write function (xi,….xn) = y. If parties want to use a randomized function to randomize their inputs, they evaluate a function:
Function (xi,….xn: r) = (yi,…,yn) |
where, r is a uniformly random value unknown by all parties.
In other words the inputs, outputs and intermediate data all only are available in encrypted form throughout the entire process; hence no individual finds it feasible to deduce the unencrypted form of any of those data. At the same time each party and indeed any outside observer, is convinced that the computation was carried out correctly and a super-threshold subset of the parties can decrypt any particular data. SMC can be used to address Yao’s millionaire’s problem, the private information retrieval problem, privacy-preserving statistical database and privacy preserving data mining electronic voting scheme and sealed bid auction.
Goldreich et al. (1987) extend Yao’s idea based on cryptographic intractability assumptions. Many works implement the SMC by a similar methodology method: the computation problem is first represented as a combinatory circuit and then the parties run a short protocol for every gate in the circuit and on the complexity depends on the size of the circuit which depends on the size of the input domain.
Ben-Or et al. (1988) first give a SMC protocol based on Shamir secret-sharing of each bit. They and Chaum et al. (1988) stated that every function can be securely computed with perfect security in presence of an adaptive, passive adversary, if and only if the adversary corrupts less than n/2 (n/3) parties, respectively. Gennaro et al. (1998) presented a fast-track multiparty computation protocol based on homomorphic commitments.
Jakobsson and Juels (2000) presented an efficient and simple SMC based on mix and match, does not use verifiable secret sharing characterizing nearly all previous protocols in the study. It involves producing by mixnet, an equivalent logic circuit but with randomly scrambled truth tables for the logic gates; this circuit is not known to any individual party because the truth tables are stored in encrypted form; we match the input-bit of each logic gate with the output-bit of its predecessor gate, by means of distributed plaintext-equality-tests; Finally, the last gate produces the output bit in encrypted form; the players jointly decrypt it. The joint decryptions need to be accompanied by ZK-proofs by each player that they are correctly doing their part in each. The whole mix and match protocol requires O(QG) modular exponentiations worth of work to produce a verification of circuit operation.
Beerliova and Hirt (2008) improved the protocol (Hirt et al., 2000) from efficiency and the protocol (Hirt and Nielsen, 2006) from security, use the hyper-invertible matrices, neither two-dimensional sharing nor probabilistic checks, to construct a perfectly secure multi-party protocol with optimal resilience and linear communication complexity. Their protocol provides perfect security against an active, adaptive adversary corrupting t<n/3 players. Bogetoft et al. (2008) give an first large-scale practical experiment with using MPC to implement a secure auction.
Du and Atallah (2001) survey SMC application on privacy-preserving database query, scientific computations, intrusion detection, statistical analysis, geometric computations and data mining. Cramer et al. (2008) survey some known general results that describe when secure multi party computation is possible and protocols for commitment and verifiable secret sharing for building secure multiparty protocols.
Deniable authentication protocol: Deniable authentication protocols allow a sender to authenticate a message for a receiver, in a way that the receiver can not convince a third party that such authentication (or any authentication) ever took place. Deniable authentication has two characteristics that differ from traditional authentication.
A practical secure deniable authentication protocol should have the following properties:
Completeness or authentication; strong deniability (Raimondo and Gennaro, 2005); weak deniability (Raimondo and Gennaro, 2005). Security of forgery attack (Shao, 2004); security of impersonate attack (Shao, 2004); security of compromising session secret attack (Lee et al., 2007); security of man-in-the-middle attack (Han et al., 2005).
The deniable authentication protocol can fall into two categories: interactive deniable authentication protocols and non-interactive deniable authentication protocols.
Dwork et al. (1998) proposed an interactive deniable authentication protocol based on the concurrent zero-knowledge proof. Aumann and Rabin (1998) proposed an interactive deniable authentication protocol based on factoring problem. Deng et al. (2001) proposed two interactive deniable authentication protocols based on factoring and the discrete logarithm problem, respectively. Zhu et al. (2006) analyze the security of (Deng et al., 2001; Aumann and Rabin, 1998) and point out they are vulnerability to the person-in-the-middle attack. Fan et al. (2002) proposed another simple interactive deniable authentication protocol based on the Diffie-Hellman key distribution protocol. Han et al. (2005) proposed an interactive deniable authentication protocol resisting man-in-the-middle attack based on Diffie-Hellman key exchange protocol. Feng and Ma (2007) proposed a concurrent deniable authentication based on witness indistinguishable which can support strong deniability.
The interactive deniable authentication protocols are inefficient. Hence several non-interactive deniable authentication protocols are proposed. Fan et al. (2002) proposed a non-interactive deniable authentication protocol based on Diffie-Hellman algorithm. Shao (2004) points out there are three weakness in study (Fan et al., 2002) and give an improved a generalized ElGamal signature scheme. Lu and Cao (2005a, b) proposed a non-interactive deniable authentication protocol based on bilinear pairings and factoring, respectively. Lee et al. (2007) pointed that protocols (Shao, 2004; Lu and Cao, 2005a, b) can not protect against compromising session secret attack and introduce a new deniable authentication protocol using generalized El-Gamal signature scheme. But these non-interactive deniable authentication protocols have not strong deniability.
Meng (2009a) developed a non-interactive deniable authentication protocol based on discrete logarithm problem to support strong deniability. Meng protocol is described in the following part:
Initialized phrase: The Authority performs the following steps:
Firstly, choose a large prime numbers p; secondly, compute a random multiplicative generator element g in finite field of p elements: GF(p); thirdly, send the g, p to the bullet board.
The sender performs the following steps:
Firstly, pick a serial random numbers ![]() i = 1,….,l; secondly, compute his public key by
i = 1,….,l; secondly, compute his public key by ![]() i = 1,….,l and thirdly, send the RPU to the bullet board.
i = 1,….,l and thirdly, send the RPU to the bullet board.
The receiver performs the following steps:
Firstly, pick a random number x ∈ Uzp–1 RPR = x; secondly, compute his public key by: RPU = gx (mod p) and thirdly, send the RPU to the bullet board.
When finishing the initialized phrase the sender has serial public and private keys ![]() , at the same time receiver has his public and private keys (RPU, RPR).
, at the same time receiver has his public and private keys (RPU, RPR).
Execution of protocol phrase
The sender: Firstly, chooses randomly a public and private key ![]() . The private and public keys of each run of the propose protocol are different.
. The private and public keys of each run of the propose protocol are different.
Secondly, computes: ![]() and forget
and forget ![]() after a certain time. K = (RPU)δ mod p hash (k||m) = MAC
after a certain time. K = (RPU)δ mod p hash (k||m) = MAC
Thirdly, sends ![]() to the receiver.
to the receiver.
The receiver: Firstly, compute:
Secondly, verifies hash (k' || m) = MAC, if the result is true, the receiver accepts it. Otherwise the receiver rejects it.
INTERNET VOTING MODEL
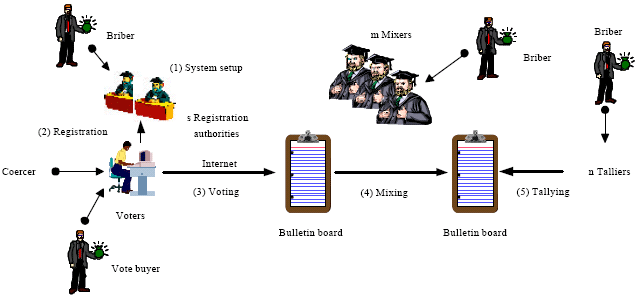
The internet voting model in Fig. 1 that consists of four phases: system set up phase, registration phase, voting phase and tally phase. In the election the briber wants to make the authority accept the bribe. In order to deal with the situation, threshold encryption is used in the internet voitng system.
System set up phase: Authorities set up the voting system. At the same time authorities and voters generate the public/private keys. The private keys of voter and authorities are secret.Authorities generate the ballot and send the ballot and its digital signature to bulletin board.
Registration phase: Voter gets his credential through a secure channel and the ballot from the bulletion board. At this phase coercer may be force the voter to vote a special ballot. Voter can use some technologies to generate a fake credential and use it to produce a ballot which the coercer can not verify.
Voting phase: Voter prepares an encrypted ballot and posts it on a bulletin board in an authenticated manner. Then multiple independent mix servers shuffle the posted ballots sequentially in a verifiable way such that the voter-vote relationship is lost.
 | |
| Fig. 1: | Internet voting model |
Tallying phase: After the mixing process is finished, multiple tally servers jointly open encrypted ballots using threshold decryption protocol and publish the result of tallying.
RECEIPT-FREENESS
Receipt-freeness is introduced by Benaloh and Tuinstra, (1994) and Niemi and renvall (1995) independently. In the receipt-free voting protocol the voter can not produce a receipt to prove that he votes a special ballot, even if the voter wishes to do so. The property of receipt-freeness ensures that an attacker can not determine exact voter behavior and therefore cannot coerce a voter by dictating her choice of candidate. It also protects against vote buying by preventing a potential vote buyer from obtaining proof of the behavior of voters; voters can thereby pretend to sell their votes, but defraud the vote buyer.
Many experts have done work on how to implement receipt-freeness. The mechanism can fall into two categories: one is with strong physical assumptions. The other is with weak physical assumption. Now, we know that the weakest physical assumption is one way anonymous channel.
Generally, the development of physical assumption based Internet voting protocols with receipt-freeness is from strong physical assumption to weak physical assumption during the last decades. However, in 2006 Rivest argued that it is impossible to implement receipt-freeness without physical assumptions. In the following, we survey the receipt-free voting protocols.
The survey processes in three different lines: The first line is to analyze the voting protocols according to whether they use strong or weak physical assumptions. The second line follows the trace of emergence and developments of receipt-free voting protocols. The third line is to analyze the features what concrete technologies are used during development.
Implementation with strong physical assumptions: Based on voting booth that physically guarantees secret communication between the authorities and each voter, Benaloh and Tuinstra, (1994) proposed two voting protocols using homomorphic encryptions. The first one is a single authority voting protocol which, while being receipt-free, fails to maintain vote secrecy. The second protocol is a multi authority scheme achieving vote secrecy. The basic idea of the multiple-authority protocol (Benaloh and Tuinstra, 1994) is to have every voter secretly share his vote among the authorities with secret-sharing scheme, who then add up the shares and interpolate the tally. Hirt and Sako (2000) point out that the multiple-authority protocol (Benaloh and Tuinstra, 1994) is not receipt-freeness. In the protocol (Benaloh and Tuinstra, 1994), the voter uses the secret-sharing scheme to share the part of ballot in each authority. At the same time they use the cut-and-choose proof to prove that the part of ballot is valid. If want to obtain a receipt, the voter could select an arbitrary string s and set the string (b0, b1,…,bn) as the bitwise output of a known cryptographic hash function for that string s. Then, s is a receipt of the vote b0. At the same time, independently, Niemi and renvall (1995) use a physical voting booth where a voter performs multiparty computation with all centers to implement receipt-freeness.
Motivated by the study of Benaloh and Tuinstra, (1994) and Sako and Kilian (1995) proposed the first receipt-free voting scheme based on mix-type anonymous channel. Receipt-freeness is achieved by assuming untappable one-way private channels through the center can send a voter a message, since the voter can not prove its vote to adversary. Use of the untappable channels however, creates the possibility for disputes between the voter and the authority, over a communication and also makes the scheme less practical.
Michels and Horster (1996) analyzed the protocol of Sako and Kilian (1995) and find that the coercer must not collude with any center. Otherwise, its robustness is lost. More seriously, it is further pointed out that the privacy of votes can not be guaranteed, if only one Mix-center is honest. Hence, under the commonly used assumption that only one Mix-center must be honest; the voting scheme is insecure unless modified.
By applying the idea of Sako and Kilian (1995) and assuming the physical assumption that the existence of secret one-way communication channels from the authorities to the voters, Hirt and Sako (2000) proposed a novel generic construction for introducing receipt-freeness into a voting scheme based on homomorphic encryption with verifiable decryption property. The idea of construction is that: The generic construction is that for each voter the authorities jointly generate a randomly ordered list with an encryption of each valid vote. The ordering of the list is secretly conveyed and proven to the voter by deploying the technique of designated verified proofs and the voter points to the encryption of his choice. Tallying of votes is performed using the homomorphic property of the encryption function.
Baudron et al. (2001) also proposed a practical multi-candidate election scheme that guarantees with receipt-freeness. Their scheme is based on the Paillier cryptosystem and on zero-knowledge proof techniques. The voting schemes are very practical and can be efficiently implemented in a real system. In their scheme they mainly use the independent randomizer to implement the receipt-freeness. At the same time, they assume there is a secret communication channel between any user and a randomizer. Voters ask the independent randomizer to randomize their votes, without modifying the contents and prove that this new ciphertext encrypts the same vote as his original one with non-transferable interactive/non-interactive zero-knowledge proof or non-interactive designated-verifier proof or proof of equality of plaintext.
Magkos et al. (2001) employed an interactive honest-verifier ZK proof made by a tamper resistant smartcard, which plays the role of personal mixer, to the voter. In this scheme, voter prepares an encrypted ballot through an interactive protocol with TRR in a way that he loses his randomness but is convinced personally that the final ballot is constructed correctly. Presumably because of the simulation of this proof, they describe the proof as being non-transferable. But, Juels et al. (2005) pointed out this is not true. In particular, an adversary can stipulate that the voter engage in the proof using a challenge that the adversary has pre-selected. The proof then becomes transferable, yielding a means of receipt construction by the adversary. They also explain why deniable encryption does not solve the problem of coercion in a voting system.
Chaum (2002, 2004) use a visual cryptography to implement the receipt-freeness by introducing a special receipt. In the voting booth, the voter can see his or her choices clearly printed on the receipt. After taking it out of the booth, the voter can use it to ensure that the votes it contains are included correctly in the final tally. But, because the choices are safely encrypted using visual cryptography before it is removed from the booth, the receipt cannot be used to show others how the voter voted. The receipt can be tested for authenticity and its presence in the batch of ballots about to be tallied can be verified.
Okamoto (1996) uses the trapdoor bit commitment to develop a receipt-free voting protocol if the random number αi generated by the voter as specified. But, he points out in the study (Okamoto, 1998) that if the random number αi generated by the vote buyer/coercer, the coercer force the voter to use ![]() as the bit commitment of the voter, then the voter can not open the commitment
as the bit commitment of the voter, then the voter can not open the commitment ![]() in more than one way, because the voter does not know the value αi, hence the voting scheme is not receipt-free. Hence, Okamoto (1996) improved the voting scheme by introducing the untappable channel, or secret sharing scheme, or voting booth to make it have receipt-freeness.
in more than one way, because the voter does not know the value αi, hence the voting scheme is not receipt-free. Hence, Okamoto (1996) improved the voting scheme by introducing the untappable channel, or secret sharing scheme, or voting booth to make it have receipt-freeness.
Neff (2003) proposed an efficient voting scheme based on his shuffle mix-net protocol. Neff’s protocol is efficient and also allows write-in ballots. However, receipt-freeness in Neff’s protocol depends on, physical conditions: the voter must be monitored by an election authority so that she does not bring outside the voting booth a codebook which confirms the unique, publicly verifiable correspondence between the election codes and the voter’s preferences. If the voter succeeded in bringing the codebook out of the voting booth, she would be able to prove to another party her vote. Furthermore, procedural assumptions are also needed to prevent the voting machine to recognize whether a user is a voter or an observer-without such assumptions, cheating is possible.
Lee et al. (2003) used the Designated Verifier Re-Encryption Proof (DVRP) to implement receipt-freeness in mixnet-based electronic voting schemes. They use the tamper resistant randomizer to provide a randomization service to voter’s encrypted ballot. Due to DVRP the voter is convinced that the ballot is preserved in the final ballot, he cannot transfer the proof to others with the condition that a buyer cannot observe the very moment of voter’s voting and the communication channel between a voter and his TRR is internal, a voter cannot be coerced into casting a particular vote.
Rivest (2006) proposed a paper-based receipt-free voting protocol called three ballot voting system without cryptosystem. The idea of the three ballot voting system is that, not only can each voter verify that her vote is recorded as she intended, but she gets a receipt that she can take home that can be used later to verify that her vote is actually included in the final tally. Her receipt, however, does not allow her to prove to anyone else how she voted. One key principle of Three ballot is to vote by rows and cast by columns. The Three ballot can viewed as an array, where the voter places marks in rows corresponding to candidates, but then separates the columns and casts them separately, keeping a copy of one. Each paper ballot, called 3-ballot, contains three columns and as many rows as the candidates in a race. Each row corresponds to one candidate. In a row there are three bubbles, one bubble per column. In order to vote for a candidate A the voter has to fill exactly 2 bubbles in the row corresponding to A. In each of the other rows the voter must fill exactly one bubble. The choice which bubbles to fill in a row is arbitrary. A ballot that does not obey these rules is rejected by a checker device. If a ballot is correct, an ID is printed in each column; the ID’s in different columns are unrelated and random. Then the columns are separated; each column forms a ballot. The voter chooses one of them and gets its copy. Finally, the voter casts all his ballots into the ballot box. After opening the ballot box all ballots find inside are published on a bulletin board. The number of the votes for the candidate A is computed as m-n/3, where m is the number of ballots containing a filled bubble in the row of A and n is the total number of ballots in the ballot box. Strauss (2006) describes a dozen different problems with three-ballot voting. Strauss analyzes receipt-free and gives a attack called receipt buying. Alice and Bob are the two candidates of election. Bob cheats by buying Alice receipts. For each one, he can safely change the corresponding serial-numbered ballot in the box from an Alice mark to a Bob mark, because the voter no longer has the receipt to prove anything. Rivest points out that the voter can prevent Bob from doing this by keeping a copy of her receipt. Rivest suggests several methods that might make it easier for voters to have multiple copies of their receipts, to prevent receipt buying. Appel (2006) finds a combined attack on three ballot voting system. Cichon et al. (2008) analyzed the relation between the number of the candidates in a race and effectiveness of Strauss’ attack. They also show that in a reasonable scenario it is impossible to reconstruct voters’ preferences for a single race with two candidates. Clark et al. (2007) consider security requirements for receipts in E2E voter-verifiable voting systems, focusing on Three ballot voting system etc. Marneffe et al. (2007) have taken a formal analysis of Three ballot given under their model. They compare the capabilities of an adversary interacting with an implementation of a voting protocol to the capabilities of an adversary interacting with an ideal implementation of voting. Their analysis of Three ballot reveals the same issues (Clark et al., 2007) and a modification that avoids this problem is presented. Focusing on two-candidate races, Henry et al. (2008) determine thresholds for when the voter’s vote can be reconstructed from a receipt and when a coercer can effectively verify if a voter followed instructions by looking for pre-specified patterns on the bulletin board.They also generalize the two-candidate attack allows an adversary to take advantage of the bulletin board to increase the probability of determining a voter’s vote, given their receipt.
Chang and Lee (2006) presented an efficient and secure voting mechanism by employing Chaum’s blind signature scheme and Diffie-Hellman key exchange protocol. Due to Bi is under the protection of the shared session key k*, a common key between Registration Center and Monitor Center and Vote Counter, the voter cannot reveal mi, the marked ballot of the voter, to others. But according to our analysis, due to the application of blind signature scheme, hence the voting scheme (Chang and Lee, 2006) is not receipt-free. Because, the voter can provide the blinding factor to vote buyer.
Moran and Naor (2006) argue that they give the first receipt-free scheme to give everlasting privacy for votes: even a computationally unbounded party does not gain any information about individual votes based on the protocol (Neff, 2004).
Zwierko and Kotulski (2007) proposed an agent-based receipt-free electronic voting scheme. The security mechanisms applied in the system are based on the secure secret sharing scheme and Merkle’s puzzles (Merkle, 1978). The scheme allows the voter to verify if his/hers vote was tallied by publishing the proofs (h(g(xi), uf)), but does not enable him proving to any third party what vote was casted. The voter can present the coercer a ballot ![]() for the published hash
for the published hash ![]() . The coercer can verify that the hash is published, but he is unable to verify the claimed vote, since it is encrypted with xi. Moreover, it is easy for the voter to create a false ballot with a selected vote and a published hash, since the coercer cannot verify the proof
. The coercer can verify that the hash is published, but he is unable to verify the claimed vote, since it is encrypted with xi. Moreover, it is easy for the voter to create a false ballot with a selected vote and a published hash, since the coercer cannot verify the proof ![]() , because the function g is secret and known only to the mix, the list of produced g(xi) values is known only to TA.
, because the function g is secret and known only to the mix, the list of produced g(xi) values is known only to TA.
Wei et al. (2007) proposed a receipt-free punch-hole ballot e-voting based on homomorphic encryption and designated-verifier re-encryption proof. They use the randomizer to re-encrypt the first ballot cast by the voter. The randomizer and the voter jointly generate the final ballot for the tally. The randomizer proves to the voter that each of her first encrypted sub-ballots is reencrypted correctly in a designated-verifier manner through the untappable channels. The designated verifier proofs can be simulated by the prover. So, the proofs are only convincing to the voter and cannot be transferred to others. The randomizer adds its internal randomness to the encrypted first ballot and to the joint proofs. The voter cannot obtain any information of the randomizer's randomness so she cannot prove any link between her first ballot and her final ballot. Therefore the voter cannot construct a receipt to prove the content of her cast ballot. So the voting scheme has receipt-freeness.
Fan and Sun (2008) presented ideas for developing an effective electronic voting protocol, allowing one to greatly reduce the chances of receipt and coercibility. Their protocol depends on blind signature and dual randomization (Lei and Fan, 1998). Every voter randomly chooses a string and combines it with another string randomly selected by the authority, where the two strings are mixed and integrated into the random part of the voter’s ballot. Not only can the idea make all ballots distinct one another, but also it can prevent the coercers or vote-buyers from linking some designated ballots to their assigned strings, because that they cannot control the final values of the random parts in the ballots.
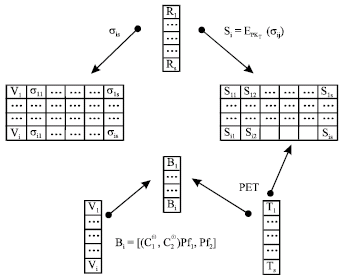
Implementation with weak physical assumptions: Juels and Jakobsson (2002) directly address the problem of achieving receipt-freeness and uncoercibility without unpractical assumptions, which does not require unstappable channels, but instead assumes voter access to an anonymous channel at some point during the voting process. The model of the voting protocol (Juels and Jakobsson, 2002) is shown in Fig. 2. The key idea behind their scheme is for the identity of a voter to remain hidden during the election process and for the validity of ballots instead to be checked blindly against a voter roll.
 | |
| Fig. 2: | Model of the voting protocol (Juels and Jakobsson, 2002) |
When casting a ballot, a voter incorporates a concealed credential. This takes the form of a ciphertext on a secret value that is unique to the voter. The secret credential is a kind of anonymous credential. To ensure that ballots are cast by legitimate voters, the tallying authority performs a blind comparison between hidden credentials and a list L of encrypted credentials published by an election registrar alongside of the plaintext names of registered voters. By means of mixing and blinding, we can check whether a concealed credential is in the list or not, without revealing which voter the credential has been assigned to. In consequence, an attacker is given a fake credential by a coerced voter. In other word the voter has the ability to generate a fake credential that the vote buyer or coercer can not find whether or not the credential is valid. Later they give a new version (Juels et al., 2005). At the same time they give the blind function another name: Plaintext Equivalence Test.
Acquisti (2004) proposed a receipt-free voting protocol based on homomorphic encryption and designated verifier proof with the physical assumption: anonymous channel. The idea is that election authorities provide shares of credentials to each voter, along with designated verifier proofs of each share’s validity. Using homomorphic encryption, the voter assembles the shares and combines them with her own vote that is cast on a public bulletin board. All messages in the bulletin board can be decrypted by a coalition of the election authorities after the voting phase of the election is completed. But according to our analysis of Acquisti protocol, we find that (1) it is not invariableness. In Acquisti protocol the voter can use per credential to vote many times. In other words the voter can use per credential to vote the same ballot many times and also can use per credential to vote different ballot many times. In the tallying phrase the author only deals with the status that the voter can use per credential to vote the same ballot many times. The other status that voter can use per credential to vote different ballot many times does not be considered. So on that status we use the search algorithm in the tallying phrase, the tally result may be different. So, it is not property of invariableness. This is an important problem. (2) Acquisti protocol is not receipt-freeness. In Acquisti protocol ![]() is send by the authority through a tappable channel. That means the vote buyer can get
is send by the authority through a tappable channel. That means the vote buyer can get ![]() and know that it is send by the authority.
and know that it is send by the authority. ![]() represents RSA encryption under vj's public key. The voter can prove that
represents RSA encryption under vj's public key. The voter can prove that ![]() is the decryption of
is the decryption of ![]() with the public key of vj and the property of RSA encryption.
with the public key of vj and the property of RSA encryption. ![]() is published on the bulletin board. Generally, voter can successfully verify the designated verifier proof
is published on the bulletin board. Generally, voter can successfully verify the designated verifier proof ![]() of equality between EV(ci,j) and the corresponding EC(ci,j). So, the voter can reveal how to generate the vote
of equality between EV(ci,j) and the corresponding EC(ci,j). So, the voter can reveal how to generate the vote ![]() that is compatible with the receipt
that is compatible with the receipt![]() and
and ![]() .
.
Chen et al. (2008) introduced the notion of linkable ring signature for designated verifiers and then use it to propose a new receipt-free electronic voting scheme. The voting scheme achieved receipt-freeness by allowing the voters to vote multi-times. Note that, when a voter buyer wants to buy a vote, even if the voter gives all his information to voter buyer, including his private key, voter buyer still can not trust him because the voter can cast another ballot in private and revoke the previous one.
Meng protocol has the properties of universal verifiability, receipt-freeness and coercion-resistance and does not use the strong physical assumptions. Applying confidentiality of voter credential and the proposed deniable authentication protocol, Meng protocol accomplishes receipt-freeness. Voter checks equality between credential from authority and credential in Bulletin Board by proof protocol that knowledge that two ciphertexts are encryption of the same plaintext ![]() . Other peoples can not check owning to the specialty of the meng deniable authentication protocol. According to the Meng deniable authentication protocol voter has the ability of generation of a fake
. Other peoples can not check owning to the specialty of the meng deniable authentication protocol. According to the Meng deniable authentication protocol voter has the ability of generation of a fake ![]() . The vote buyer can not check
. The vote buyer can not check ![]() and can not verify EV(cj). So, the vote buyer does not give the money to the voter. Hence Meng protocol is receipt-freeness. Meng (2007a) also propose an Internet voting protocol applied designated verifier proof and proof of knowledge of two ciphertexts of the same plaintext.
and can not verify EV(cj). So, the vote buyer does not give the money to the voter. Hence Meng protocol is receipt-freeness. Meng (2007a) also propose an Internet voting protocol applied designated verifier proof and proof of knowledge of two ciphertexts of the same plaintext.
According to the earlier studies, we present the results of our survey on receipt-freeness. Firstly, we give the relationship of receipt-free Internet voting protocols analyzed by us in Fig. 3a and b, which consists of two parts. Figure 3a shows that the traditional cryptographic primitives are used to develop receipt-freeness with physical assumptions. Figure 3b shows that the special cryptosystem is used to implement receipt-freeness with strong physical assumptions.
 | |
| Fig. 3: | (a, b) The relationship of Internet voting protocols with receipt-freeness. The color shade represents the strong or weak physical assumption |
Then, we present that what physical assumption is used to implement receipt-freeness and the results of analysis of receipt-freeness in Table 1.
After that, we give that what technologies are used to implement receipt-freeness in protocols analyzed by us in Table 2.
| Table 1: | The result of analyzing receipt-freeness and what physical assumptions are used |
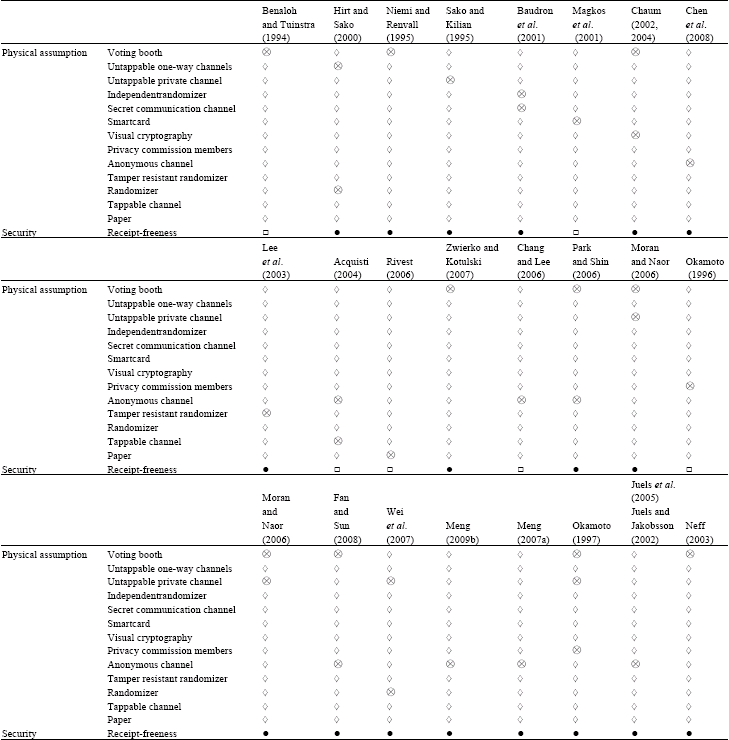 | |
| ⊗ The protocol is with physical assumption;◊The protocol is not with physical assumption, ●: The protocol has the property, □: The protocol has not the property | |
| Table 2: | Core technologies used to implement rceipt-freeness |
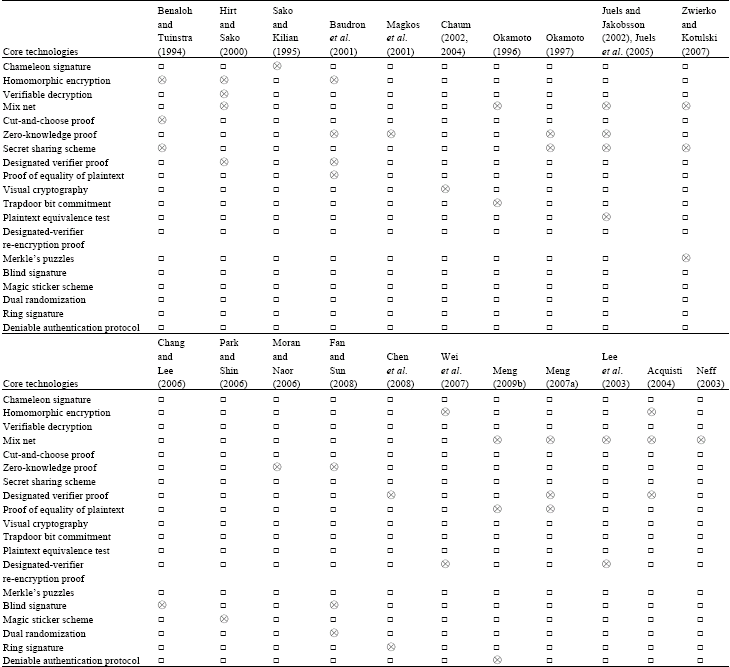 | |
| ⊗: The core technology is used, □: The core technology is not used | |
COERCION-RESISTANCE
Previous investigations of coercion-resistant voting have been concerned to a property known as receipt-freeness. Benaloh and Tuinstra, (1994) give the definition of uncoercibility: no voter should be able to convince any other participant of the value of its vote, even if the voter wishes to do so. According to the definition of uncoercibility in the study (Benaloh and Tuinstra, 1994), people think should use the notion of receipt-freeness to express the content.
Many experts have done work on how to implement coercion-resistance. The mechanism can fall into two categories: one is with strong physical assumptions. The other is with weak physical assumptions. Now we know that the weakest physical assumption is one way anonymous channel.
During the last 10 years most of coercion-resistant Internets voting protocols are developed with weak physical assumptions. In the following: we survey the coercion-resistant voting protocols.
Implementation with weak physical assumptions: Juels and Jakobsson (2002) propose the first strong definition of coercion-resistance. A coercion-resistant scheme offers not only receipt-freeness, but also defense against randomization, forced-abstention, and simulation attacks all potentially in the face of corruption of a minority of tallying authorities. Generally, the adversary may instruct targeted voters to divulge their private keys subsequent to registration, or may specify that these voters cast ballots of a particular form. If the adversary can determine whether or not voters behaved as instructed, then the adversary is capable of blackmail or otherwise exercising under influence over the election process. Hence, a coercion-resistant voting system is one in which the user can deceive the adversary into thinking that she has behaved as instructed, when the voter has in fact cast a ballot according to her own intentions. Adversary can not distinguish between the output from a vote of her choice and any vote of the voter’s choice in general. Hence, if the voter has the ability to cheat the coercer, at the same time the voting scheme is receipt-freeness, the voting scheme has the coercion-resistance. They propose a coercion-resistant electronic election based on Plaintext Equivalence test, mix net and zero knowledge proof. The key idea can be found in previous section. According to our analysis we find that it has the following problems: (1) do not defense against forced-abstention and simulation attacks and ( 2) can not support write in ballot.
Based on JCJ idea (Juels et al., 2005) and Smith (2005a) points out JCJ scheme is not secure against 1009 attack and time stamping attack and then proposed an improved coercion-resistant scheme based on secret encryptions. The scheme replaces the inefficient comparison mechanism of JCJ by a new one that computes the voting results in linear time. In addition, it includes an additional mix step in the tallying phase and uses time stamps. He performs a global blind comparison of ciphertexts instead of employing the costly plaintext equivalence test. In order to do this, the method makes deterministic fingerprints from probabilistic encryptions. This way, the fingerprints can be compared through hash tables efficiently. So, Smith’s comparison method is efficient. But Araujo et al. (2008) and Clarkson et al. (2007) point out that the method is not secure: an adversary can use the ElGamal malleability to determine whether a coerced voter gave him a valid or a fake credential. The proposed encryption function is Enc (m; z) = m2, where, z a secret key, is distributed among the tellers. But to test whether s a real private credential is, the adversary can inject a vote using s2 as the private credential. After the proposed encryption function is applied during invalid credential elimination, the adversary can test whether any submitted credential is the square of any authorized credential. If so, then s is real with high probability. Weber (2006) and Weber et al. (2007), however, pointed out weaknesses on Smith’s proposal and fixed the JCJ scheme and Smith scheme. Their method is based on the Shamir (1979) secret sharing and Pedersen (1991) distributed key generation protocol. The method works as following: first all n election authorities jointly generate a secret shared hash key z. After that, the authorities cooperatively apply their shares of z to an ElGamal ciphertext; this process blinds the plaintext inside the ciphertext.
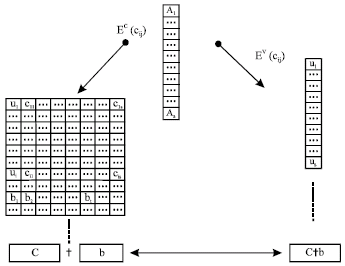 | |
| Fig. 4: | Model of the voting protocol (Acquisti 2004) |
Then, the ciphertext is decrypted, yielding a blinded plaintext (the deterministic fingerprint). Finally, after processing all ciphertexts, they can be compared without leaking information about the plaintext by using these fingerprints.
Applying some of the JJ ideas Juels and Jakobsson (2002) and Acquisti (2004) proposed a coercion-resistant voting protocol with anonymous channel. The model of the voting protocol (Acquisti 2004) is shown in Fig. 4. The idea is that election authorities provide shares of credentials to each voter, along with designated verifier proofs of each share’s validity. Using homomorphic encryption, the voter assembles the shares and combines them with her own vote that is cast on a public bulletin board. All messages in the bulletin board can be decrypted by a coalition of the election authorities after the voting phase of the election is completed. Acquisti protocol mainly applied designated verifier proof to accomplish coercion-resistance. Voter can cheat the coercer by producing a false credential. Owning to designate verifier proof the coercer can not verify the proof. It is not receipt-freeness and coercion-resistance. But according to our analysis we find that the voting scheme is not coercion-resistant. According to the definition of coercion-resistance we know that if a voting protocol is not receipt-free, it is not coercion-resistant. So we firstly point that Acquisti protocol is not receipt-freeness. In previous section we have point out that is not receipt-freeness. According to the definition of coercion-resistance it is not coercion-resistant.
Clarkson et al. (2007) proposed an electronic voting system based on JCJ ideas, called Civitas, that is coercion-resistant, universally and voter verifiable and suitable for remote voting. They argue that it the first voting system to implement a scheme proved to satisfy coercion resistance and verifiability. The key idea that is that enables voters to resist coercion and defeats vote selling, is that voters can substitute fake credentials for their real credentials, then behave however the adversary demands. To construct a fake credential, the voter locally runs an algorithm to produce fake private credential shares that, to an adversary, are indistinguishable from real shares. The faking algorithm requires the voter’s private designation key. The voter combines these shares to produce a fake private credential; the voter’s public credential remains unchanged. To construct a fake credential, a voter chooses at least one registration teller and substitutes a random group element s'i ∈ M for the share si that registration teller sent to the voter. The voter can construct a DVRP that causes this fake share to appear real to the adversary, unless the adversary has corrupted the registration teller the voter chose (in which case the adversary already knows the real share), or unless the adversary observed the channel used by the registration teller and voter during registration (in which case the adversary has seen the real proof). By trust assumption (Each voter trusts at least one registration teller and the channel from the voter to the voter’s trusted registration teller is untappable), there exist some teller and channel that the adversary does not control, so it is always possible for voters fake credentials. Kousters and Truderung (2009) point that if a registration teller refuses to provide a credential share to the voter and propose to use an additional voting authority, Civitas does not provide coercion resistance, if the goal of the coerced voter is to vote for a specific candidate in voting scheme (Clarkson et al., 2007).
Araujo et al. (2008) present another coercion- resistant voting scheme that employs some of the JCJ ideas and that computes election results in linear time based on LRSW assumption (Camenisch and Lysyanskaya, 2004). Due to LRSW assumption, the voter cannot prove to anyone else whether (r, a, b, c) is a valid credential or not, under the DDH assumption. This way, a voter over coercion can make a fake r (and also make fakes a, b, c) to deceive an adversary who will not be able to distinguish between a fake and a valid r. But they do not give the proof of coercion-resistance.
Applying some of the Acquisti (2004) ideas, Meng (2009b) present a receipt-free and coercion-resistant internet voting protocol based on non-interactive deniable authentication protocol and an improved proof protocol that two ciphertexts are encryption of the same plaintext. Meng protocol has the properties of universal verifiability, receipt-freeness and coercion-resistance and do not use the strong physical assumptions. Meng voting protocol accomplishes receipt-freeness by confidentiality of voter credential and the proposed deniable authentication protocol. Voter checks equality between credential from authority and credential in BB by proof protocol that knowledge that two ciphertexts are encryption of the same plaintext ![]() . Other peoples can not check owning to the specialty of the Meng deniable authentication protocol. According to Meng deniable authentication protocol voter has the ability of generation of a fake
. Other peoples can not check owning to the specialty of the Meng deniable authentication protocol. According to Meng deniable authentication protocol voter has the ability of generation of a fake ![]() . The vote-buyer can not check
. The vote-buyer can not check ![]() and can’t verify EV(cj). So, the vote-buyer does not give the money to the voter. So Meng protocol is receipt-freeness. According to definition of coercion-resistance, firstly the protocol is receipt-freeness and then prevents randomization attack, forced-abstention attack and simulation attack.
and can’t verify EV(cj). So, the vote-buyer does not give the money to the voter. So Meng protocol is receipt-freeness. According to definition of coercion-resistance, firstly the protocol is receipt-freeness and then prevents randomization attack, forced-abstention attack and simulation attack.
Randomization attack: Voter wants to prevent randomization attack. He can generate a false credential to cheat coercer because coercer can not recognize it true or false. Then voter can use true credential to vote a ballot. So, the protocol can prevent randomization attack.
Forced-abstention attack: According to protocol coercer can not know if voter has registered based on BB and if voter has vote. So the protocol can prevent Forced-abstention attack.
Simulation attack: Coercer can vote on voter behalf after getting private key of voter. But, we suppose that the private key of voter is secret in our protocol. So the protocol can prevent simulation attack. Meng (2007a) also propose an Internet voting protocol applied designated verifier proof and proof of knowledge of two ciphertexts of the same plaintext based the same idea.
Implementation with strong physical assumptions: Shubina and Smith (2004) proposed a voting scheme based on blind signatures and claims to be coercion resistant with voting booth, but it assumes the adversary cannot corrupt election authorities. If the adversary learns the ciphertext of a voter’s ticket, the scheme fails to be receipt-free. Their voting scheme also is not universally verifiable. Voters can verify their votes are recorded correctly, but the computation of the tally is not publicly verifiable.
Kiayias et al. (2006) developed a homomorphic voting scheme in which voters authenticate to a gatekeeper. If a malicious voting client may produce a proof of how a user voted or otherwise leak information about the voter, the voting scheme would fail to be coercion-resistant. They claim that in the future ciphertext re-randomization be used to address the flaws.
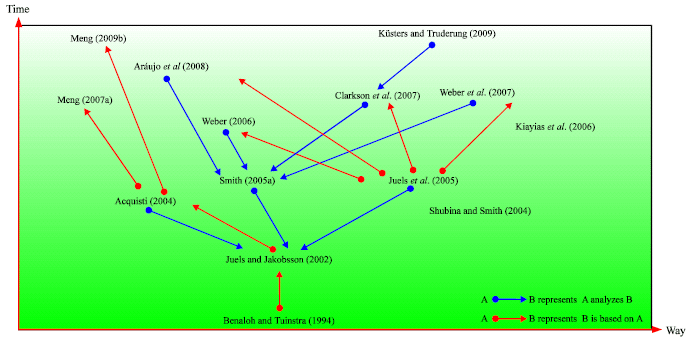 | |
| Fig. 5: | The relationship of internet voting protocols with coercion-resistance. The color shade represents the strong or weak physical assumption |
| Table 3: | The result of analyzing coercion-resistance and what physical assumptions are used |
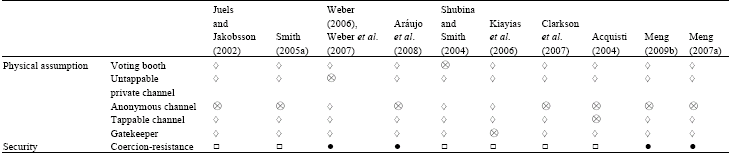 | |
| ⊗: The protocol is with physical assumption ◊: The protocol is not with physical assumption, ●: The protocol has the property. □: The protocol has not the property | |
| Table 4: | Core technologies used to implement coercion-resistance |
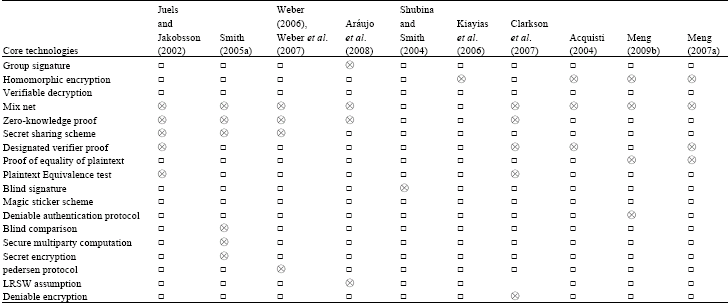 | |
| ⊗: The core technology is used, □: The core technology is not used | |
According to the result of earlier study, we firstly present the relationship of coercion-resistant Internet voting protocols analyzed by us in Fig. 5. Then we present what physical assumption is used to develop coercion-resistance and the result of analysis of coercion-resistance in Table 3. After that, in Table 4, we can find that what technologies are used to design coercion-resistance in the voting protocols.
FORMAL PROOF
Formal methods are an important tool for designing an implementing secure cryptographic protocol. By applying techniques concerned with the construction and analysis of models and proving that certain properties hold in the context of these models, formal methods can significantly increase one’s confidence that a protocol will meet its requirements in the real world.
The development of formal methods has started in 1980s (Hoare, 1985; Burrows et al., 1989, 1990; Blum and Micali, 1984; DeMillo et al., 1982; Dolev and Yao, 1983; Merritt, 1983; Yao, 1982b). The field matured considerably in the 1990s. Some of the methods rely on rigorous but informal frameworks, sometimes supporting sophisticated complexity-theoretic definitions and arguments. Others rely on formalisms specially tailored for this task. Yet others are based on strand space (Thayer et al., 1998), spi calculus (Abadi and Gordon, 1999); mur φ (Mitchell et al., 1997), Kessler and Neumann (1998) logic, applied pi calculus (Abadi and Fournet, 2001), sometimes in the context of various theorem-proving tools (Abadi and Gordon, 1999; Gray et al., 1997; Lincoln et al., 1998; Lynch, 1999; Paulson, 1998; Chothia et al., 2007; Blanchet, 2001; Backes et al., 2008).
Here, we research the formal proof on receipt-freeness and coercion-resistance. The research is carried through in two different lines: The first line traces the developments of formal proof on receipt-freeness and coercion-resistance. The second line is to analyze what formal methods are used with formal proof.
Delaune et al. (2006a) have done a pathbreaking work on proposing the formal definition of receipt-freeness and coercion-resistance based on applied pi calculus. Their formal model is based on Dolev and Yao (1983) abstaction.
Receipt-freeness: A voting protocol is receipt-free if exist a closed plain process V', satisfying the conditions below:
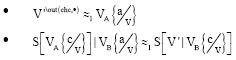 |
They formalize receipt-freeness as an observational equivalence. The idea is that if the attacker can not find if arbitrary honest voters VA and VB exchange their votes, then in general he can not know anything about how VA (or VB) voted. This definition is robust even in situations where the result of the election is such that the votes of VA and VB are necessarily revealed. They also assume that the voter cooperates with the coercer by sharing secrets, but the coercer cannot interact with the voter to give her some prepared messages.
Coercion-resistance: A voting protocol is coercion-resistance if there have a closed extended process V' and a strict evaluation context C such that:
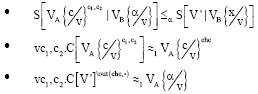 |
But Jonker Hugo et al. (2006) point out that the formal model (Delaune et al., 2006a) offers little help to identify receipts when receipts are present. Hence, Jonker Hugo et al. (2006) presented a new formal method, which uses the process algebra, to analyze receipts based on their informal definition: a receipt r is an object that proves that a voter v cast a vote for candidate c. This means that a receipt r has the following properties: (R1) r can only have been generated by v. (R2) r proves that v chose candidate c. (R3) r proves that v cast her vote. Jonker and de Vink provide a generic and uniform formalism that captures a receipt. Jonker and de Vink formal model is also simpler than Delaune'formal model. They use the formalism to analyze the voting protocols (Benaloh and Tuinstra, 1994; Sako and Kilian, 1995; Hirt and Sako, 2000; Aditya et al., 2004; Hubbers et al., 2005). Meng (2007b) analyzes receipt-feeness of the protocols (Fujioka et al., 1992; Cramer et al., 1997; Juels and Jakobsson, 2002; Acquisti 2004) based on formalism (Jonker Hugo et al., 2006).
About definition of receipt proposed by Jonker Hugo et al. (2006) and Meng (2009c) argues it is worth discussing. Firstly about (R1) r can only have been generated by v, in some voting protocol one part of receipt is generated by the authority, not generated by voter. Secondly, they give the following auxiliary receipt decomposition functions: α: Rcpt → AT, which extracts the authentication term from a receipt. Authentication term should be the identification of voter. Thirdly the author does not prove the generic and uniform formalism that is right in their study. Finally, they use a special notion, it difficult to use and generalize it. Hence Meng gives a formal logic framework for receipt-freeness based on Kessler and Neumann (1998) logic and apply it to analyze the voting protocol (Fujioka et al., 1992).
Knowledge based logics have been also used in the studies (Jonker and Pieters, 2006; Baskar et al., 2007; Van Eijck and Orzan, 2007) to formally analyze the security properties of e-voting protocol. Jonker and Pieters (2006) formalize the concept of receipt-freeness from the perspective of a anonymity approach in epistemic logic which offers, among others, the possibility to write properties allowing to reason about the knowledge of an agent a of the system with respect to a proposition p. They classify receipt-freeness into two types: weak receipt-freeness and strong receipt-freeness. Weak receipt-freeness implies that the voter can not prove to the vote buyer that she sent message m during the protocol, where m is the part of a message representing the vote. Here, no matter what information the voter supplies to the vote buyer, any vote in the anonymity set is still possible. In other words, for all possible votes, the vote buyer still suspects that the voter cast this particular vote; or: the vote buyer is not certain she did not cast this vote. Baskar et al. (2007) give the formal definition of secrecy, receipt-freeness, fairness, individual verifiability based on knowledge based logic and analyze receipt-freeness of the voting protocol (Fujioka et al., 1992). Eijck and Orzan (2007) used dynamic epistemic Logic to model security protocols and properties, in particular anonymity properties.They apply it to the voting scheme (Fujioka et al., 1992) and find the three phases should be strictly separated, otherwise anonymity is compromised. Mauw et al. (2007) used the process algebra to analyze the data anonymity of the voting scheme (Fujioka et al., 1992). Talbi et al. (2008) use ADM logic to specify fairness, eligibility, individual verifiability and universal verifiability and analyze the voting protocol (Fujioka et al., 1992). Their goal is to verify these properties against a trace-based model.
Groth (2004) evaluates the voting scheme based on homomorphic threshold encryption with universal composability framework. He formalizes the privacy, robustness, fairness and accurcy.
According to the above reviews we present the result of analysis in Table 5-7. We can find that what formal methods are used to analyze the receipt-freeness and coercion-resistance in Table 5. The security properties formally defined can be found in Table 6. In Table 7, we can find the result of analysis of the security properties.
| Table 5: | The formal methods used in definition of receipt-freeness and coercion-resistance |
 | |
| ⊗: The formal method is used, □ :The formal method is not used | |
| Table 6: | The properties formally defined |
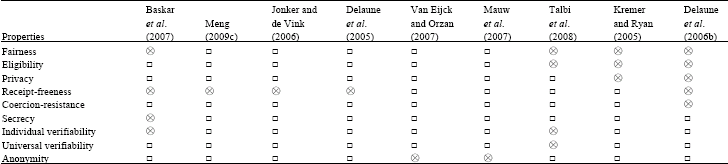 | |
| ⊗: The property is formally defined, □ :The property is not formally defined | |
| Table 7: | Formally analyzing receipt-freeness in the Internet voting protocol |
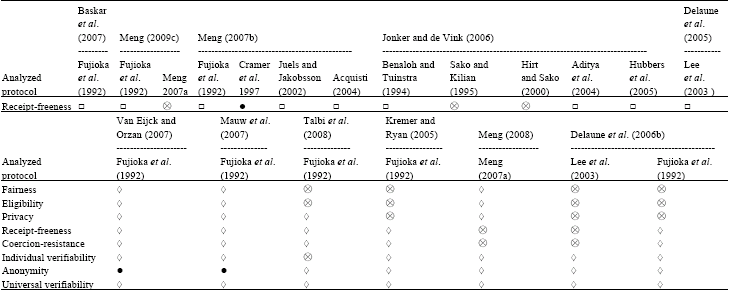 | |
| ⊗: Protocol has the property;□: Protocol has not the property; ●: Protocol has the property with some condition, ◊: Property is not analyzed | |
CONCLUSION AND THE FUTURE WORKS
Receipt-freeness and coercion-resistance play an important role in election. To present knowledge, the previous surveys do not discuss deeply the state-of-art of receipt-freeness and coercion-resistance. Hence, it is absolutely necessary to survey the state-of-art of receipt-freeness and coercion-resistance.
In this study, we first briefly discuss the development status of core cryptographic primitives related to implementation of receipt-freeness and coercion- resistance. Then the typical deniable encryption scheme (Klonowski et al., 2008) is analyzed and improved. The state-of-art of receipt-freeness and coercion-resistances presented based on the Internet voting model proposed by us. Finally, the status in quo of formal analysis of receipt-freeness and coercion-resistance is reviewed.
The future study on receipt-freeness and coercion-resistance are listed in the following part:
| • | There are two ways on the implementation of receipt-freeness and coercion-resistance. On way is implementation without physical assumptions. In this way, we find that now the weakest physical assumption is the one way anonymous channel. People can focus on proposing a secure intenet voting protocol without physical assumption. The other way is implementation with physical assumption, but without traditional cryptographic technology. In this way, people can focus on proposing a practical efficient secure Internet voting protocol |
| • | The formal analysis of coercion-resistance is not enough and is a challenging work |
| • | There are works on the formal analysis of receipt-freeness and coercion-resistance. But, the analysis of the receipt-freeness and coercion- resistance is not done by automated tool. The automated tool that can be used has not the ability to analyze these complicated secure protocols |
| • | The efficiency of voting protocol based on SMC is low. There are some works on improvement the efficiency of the voting protocol |
| • | People have proposed many Internet voting protocols. But the development of Internet voting system base on the proposed protocol is few |
REFERENCES
- Abadi, M. and A.D. Gordon, 1999. A calculus for cryptographic protocols: The spi calculus. Inform. Comput., 148: 1-70.
CrossRefDirect Link - Abadi, M. and C. Fournet, 2001. Mobile values, new names and secure communication. Proceedings of the 28th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, London, UK., January 17-19, 2001, ACM New York, USA., pp: 104-115.
CrossRefDirect Link - Abe, M. and H. Imai, 2003. Flaws in some robust optimistic mix-nets. Proceedings of the 8th Australasian Conference on Information Security and Privacy, July 9-11, 2003, Wollongong, Australia, pp: 39-50.
CrossRef - Acquisti, A., 2004. Receipt-free homomorphic elections and write-in voter verified ballots. Technical Report 2004/105, International Association for Cryptologic Research, May 2, 2004 and Carnegie Mellon Institute for Software Research International, CMU-ISRI-04-116, 2004. http://www.heinz.cmu.edu/~acquisti/papers/acquisti-.
- Adida, B. and D. Wikstrom, 2007. How to shuffle in public. Proceedings of the 4th Theory of Cryptography Conference, February 21-24, 2007, Amsterdam, The Netherlands, pp: 555-574.
CrossRef - Aditya, R., B. Lee, C. Boyd and E. Dawson, 2004. An efficient mixnet-based voting scheme providing receipt-freeness. Lecture Notes Comput. Sci., 3184: 152-161.
Direct Link - Backes, M., C. Hritcu and M. Maffei, 2008. Automated verification of remote electronic voting protocols in the applied Pi-calculus. Proceedings of the 21st Computer Security Foundations Symposium, June 23-25, 2008, IEEE Computer Society, Washington, DC, pp: 195-209.
Direct Link - Baek, J., R. Safavi-Naini and W. Susilo, 2005. Universal Designated Signature Proof (or How to Efficiently Prove the Knowledge of a Signature). In: Advances in Cryptology-ASIACRYPT, Roy, B. (Ed.). Springer-Verlag, Berlin Heidelberg, pp: 644-661.
CrossRef - Baskar, A., R. Ramanujam and S.P. Suresh, 2007. Knowledge-based modelling of voting protocols. Proceedings of the 11th Conference on theoretical Aspects of Rationality and Knowledge, June 25-27, 2007, Brussels, Belgium, pp: 62-71.
Direct Link - Baudron, O., P.A. Fouque, D. Pointcheval, G. Poupard and S. Jacques, 2001. Practical multi-candidate election system. Proceedings of the Annual ACM Symposium on Principles of Distributed Computing, August 26-29, 2001, ACM, New York, USA., pp: 274-283.
CrossRefDirect Link - Beerliova, Z. and M. Hirt, 2008. Perfectly-Secure MPC with Linear Communication Complexity. In: Theory of Cryptography, Canetti, R. (Ed.). Springer-Verlag, Berlin Heidelberg, pp: 213-230.
CrossRef - Benaloh, J. and D. Tuinstra, 1994. Receipt-free secret-ballot elections (extended abstract). Proceedings of the 26th Annual ACM Symposium on theory of Computing, May 23-25, 1994, Montreal, Quebec, Canada, pp: 544-553.
Direct Link - Bender, A., J. Katz and R. Morselli, 2006. Ring Signatures: Stronger Definitions and Constructions Without Random Oracles. In: Theory of Cryptography, Halevi, S. and T Rabin (Eds.). Springer-Verlag, Berlin Heidelberg, pp: 60-79.
CrossRef - Bender, A., J. Katz and R. Morselli, 2009. Ring signatures: Stronger definitions and constructions without random oracles. J. Cryptol., 22: 114-138.
CrossRefDirect Link - Ben-Or, M., S. Goldwasser and A. Wigderson, 1988. Completeness theorems for non-cryptographic fault-tolerant distributed computation. Proceedings of the 20th Annual ACM Symposium on Theory of Computing, May 2-4, 1988, Chicago, Illinois, United States, pp: 1-10.
CrossRefDirect Link - Blanchet, B., 2001. An efficient cryptographic protocol verifier based on prolog rules. Proceedings of the 14th IEEE Workshop on Computer Security Foundations, June 11-13, 2001, IEEE Computer Society, Washington, DC., pp: 82-96.
Direct Link - Burrows, M., M. Abadi and R. Needham, 1990. A logic of authentication. ACM Trans. Comput. Syst., 8: 18-36.
CrossRef - Camenisch, J. and A. Lysyanskaya, 2004. Signature Schemes and Anonymous Credentials from Bilinear Maps. In: Advances in Cryptology-CRYPTO 2004, Franklin, M. (Ed.). Springer-Verlag, Berlin Heidelberg, pp: 56-72.
CrossRef - Canetti, R. and R. Gennaro, 1996. Incoercible multiparty computation. Proceedings of the 37th Annual Symposium on Foundations of Computer Science, October 14-16, 1996, Burlington, VT., USA., pp: 504-513.
CrossRef - Cao, Z.F., H.J. Zhu and R.X. Lu, 2006. Provably secure robust threshold partial blind signature. Sci. China Ser. F: Inform. Sci., 49: 604-615.
CrossRefDirect Link - Chaum, D.L., 1981. Untraceable electronic mail, return addresses and digital pseudonyms. Commun. ACM, 24: 84-88.
CrossRef - Chaum, D., 1985. Security without identification: Transaction systems to make big brother obsolete. Commun. ACM, 28: 1030-1044.
CrossRefDirect Link - Chaum, D., 1990. Zero-Knowledge Undeniable Signatures. In: Advances in Cryptology-Eurocrypt `90, Damgard, I.B. (Ed.). Springer-Verlag, Berlin Heidelberg, pp: 458-464.
CrossRef - Chaum, D., 2004. Secret-ballot receipts: True voter-verifiable elections. IEEE Security Privacy, 2: 38-47.
CrossRefDirect Link - Chaum, D., C. Crepeau and I. Damgard, 1988. Multiparty unconditionally secure protocols. Proceedings of the 20th Annual ACM Symposium on Theory of Computing, May 2-4, 1988, Chicago, Illinois, United States, pp: 11-19.
Direct Link - Chaum, D. and H. Van Antwerpen, 1990. Undeniable Signatures. In: Advances in Cryptology Crypto`89, Brassard, G. (Ed.). Springer-Verlag, Berlin Heidelberg, pp: 212-216.
CrossRef - Chen, G., C. Wu, W. Han, X. Chen, H. Lee and K. Kim, 2008. A new receipt-free voting scheme based on linkable ring signature for designated verifiers. Proceedings of the 2008 International Conference on Embedded Software and Systems Symposia, July 29-31, 2008, IEEE Computer Society, Washington, DC, pp: 18-23.
CrossRef - Chothia, T., S. Orzan, J. Pang and M.T. Dashti, 2007. A Framework for Automatically Checking Anonymity with μCRL. In: Trustworthy Global Computing, Montanari, U. D. Sannella and R. Bruni (Eds.). Springer-Verlag, Berlin Heidelberg, ISBN-13: 978-3-540-75333-9, pp: 301-318.
CrossRef - Cichon, J., M. Kutyłowski and B. Glorz, 2008. Short Ballot Assumption and Threeballot Voting Protocol. In: SOFSEM 2008: Theory and Practice of Computer Science, Geffert, V. et al. (Eds.). Springer-Verlag, Berlin Heidelberg, pp: 585-598.
CrossRef - Cramer, R., I. Damgard and B. Schoenmakers, 1994. Proofs of partial knowledge and simplified design of witness hiding protocols. Proceedings of the 14th Annual International Cryptology Conference on Advances in Cryptology, August 21-25, 1994, IEEE Xplore, London, pp: 174-187.
Direct Link - Cramer, R., R. Gennaro and B. Schoenmakers, 1997. A Secure and Optimally Efficient Multi-Authority Election Scheme. In: Trustworthy Global Computing, Fumy, W. (Ed.). Springer-Verlag, Berlin Heidelberg, pp: 103-118.
CrossRef - Desmedt, Y. and M. Yung, 1991. Weakness of Undeniable Signature Schemes. In: Advances in Cryptology EUROCRYPT '91, Davies D.E. (Ed.). Springer-Verlag, Berlin Heidelberg, pp: 205-220.
CrossRef - Desmedt, Y. and K. Kurosawa, 2000. How to Break a Practical MIX and Design a New One. In: Advances in Cryptology-EUROCRYPT 2000, Preneel, B. (Ed.). Springer-Verlag, Berlin Heidelberg, pp: 557-572.
CrossRef - Delaune, S., S. Kremer and M.D. Ryan, 2006. Coercion-resistance and receipt-freeness in electronic voting protocol. Proceedings of the 19th Computer Security Foundations Workshop, July 5-7, 2006, Venice, Italy, pp: 28-42.
CrossRef - DeMillo, R.A., N.A. Lynch and M.J. Merritt, 1982. Cryptographic protocols. Proceedings of the 14th Annual ACM Symposium on theory of Computing, May 5-7, 1982, San Francisco, California, United States, pp: 383-400.
Direct Link - Du, W. and M.J. Atallah, 2001. Secure multi-party computation problems and their applications: A review and open problems. Proceedings of the 2001 Workshop on New Security Paradigms, September 10-13, 2001, Cloudcroft, New Mexico, pp: 13-22.
Direct Link - Dwork, C., M. Naor and A. Sahai, 1998. Concurrent zero-knowledge. Proceedings of the 30th Annual ACM Symposium on Theory of Computing, May 24-26, 1998, USA., pp: 409-418.
CrossRef - Fan, C.I. and W.Z. Sun, 2008. An efficient multi-receipt mechanism for uncoercible anonymous electronic voting. Math. Comput. Modell., 48: 1611-1627.
CrossRefDirect Link - Fan, L., C.X. Xu and J.H. Li, 2002. Deniable authentication protocol based on Diffie-Hellman algorithm. Elect. Lett., 38: 705-706.
CrossRef - Fujioka, A., T. Okamoto and K. Ohta, 1992. A practical secret voting scheme for large scale elections. Proceedings of the Workshop on the Theory and Application of Cryptographic Techniques: Advances in Cryptology, December 13-16, 1992, Queensland, Australia, pp: 244-251.
CrossRefDirect Link - Furukawa, J. and K. Sako, 2001. An efficient scheme for proving a shuffle. Proceedings of the 21st Annual International Cryptology Conference on Advances in Cryptology, August 19-23, 2001, Springer-Verlag, London, UK., pp: 368-387.
Direct Link - Furukawa, J., 2005. Efficient and verifiable shuffling and shuffle-decryption. IEICE Trans. Fundam. Elect. Commun. Comput. Sci., 88: 172-188.
CrossRefDirect Link - Galbraith, S. and W. Mao, 2003. Invisibility and anonymity of undeniable and confirmer signatures. Proceedings of the Cryptographers` Track at the RSA Conference 2003, April 13-17, 2003, San Francisco, CA., USA., pp: 80-97.
CrossRef - Gennaro, R., M.O. Rabin and T. Rabin, 1998. Simplified VSS and fast-track multiparty computations with applications to threshold cryptography. Proceedings of the 70th Annual ACM Symposium on Principles of Distributed Computing, June 28-July 2, 1998, Puerto Vallarta, Mexico, pp: 101-111.
Direct Link - Gao, H.M., X.F. Chen and Y.M. Wang, 2003. A new (t,N-2) resilience mix net. Chinese J. Comput., 26: 1361-1365.
Direct Link - Goldreich, O., S. Micali and A. Wigderson, 1987. How to play any mental game-a completeness theorem for protocols with honest majority. Proceedings of the 19th ACM Symposium on the Theory of Computing, May 25-27, 1987, New York, USA., pp: 218-229.
CrossRef - Golle, P., S. Zhong, D. Boneh, M. Jakobsson and A. Juels, 2002. Optimistic mixing for exit-polls. Proceedings of the 8th International Conference on the theory and Application of Cryptology and Information Security: Advances in Cryptology, December 1-5, 2002, Springer-Verlag, London, UK., pp: 451-465.
Direct Link - Gray, J.W., K.F. Epsilon and K.S. Lui, 1997. Provable security for cryptographic protocols-exact analysis and engineering applications. Proceedings of the 10th Computer Security Foundations Workshop, June 10-12, 1997, IEEE Xplore, London, pp: 45-58.
CrossRef - Groth, J., 2003. A verifiable secret shuffle of homomorphic encryptions. Proceedings of the 6th International Workshop on theory and Practice in Public Key Cryptography: Public Key Cryptography, Jane 6-8, 2003, Springer-Verlag London, UK., pp: 145-160.
Direct Link - Groth, J., 2004. Evaluating Security of Voting Schemes in the Universal Composability Framework. In: Applied Cryptography and Network Security, Jakobsson, M., M. Yung and J. Zhou (Eds.). Springer-Verlag, Berlin Heidelberg, pp: 46-60.
CrossRef - Han, S., W.Q. Liu and E. Chang, 2005. Deniable authentication protocol resisting man-in-the-middle attack. Proceedings of the World Academy of Science, Engineering and Technology, January 2005, PWASET, pp: 1-4.
Direct Link - Hirt, M. and K. Sako, 2000. Efficient receipt-free voting based on homomorphic encryption. Proceedings of the International Conference on the Theory and Application of Cryptographic Techniques, May 14-18, 2000, Bruges, Belgium, pp: 539-556.
Direct Link - Hirt, M., U. Maurer and B. Przydatek, 2000. Efficient Secure Multiparty Computation. In: Advances in Cryptology-ASIACRYPT 2000, Okamoto, T. (Ed.). Springer-Verlag, Berlin Heidelberg, pp: 143-161.
CrossRef - Hirt, M. and J.B. Nielsen, 2006. Robust Multiparty Computation with Linear Communication Complexity. In: Advance in Cryptilogy-CRYPTO 2006, Springer-Verlag, Berlin Heidelberg, pp: 463 482.
CrossRef - Huang, X.Y., W. Susilo, Y. Mu and F. Zhang, 2008. Short designated verifier signature scheme and its identity-based variant. Int. J. Network Security, 6: 82-93.
Direct Link - Hubbers, E., B. Jacobs and W. Pieters, 2005. RIES-internet voting in action. Proceedings of the 29th Annual International Computer Software and Applications Conference, July 26-28, 2005, IEEE Computer Society, Washington, DC., pp: 417-424.
Direct Link - Jakobsson, M., 1998. A practical mix. Proceedings of the International Conference on the Theory and Application of Cryptographic Techniques, May 31-June 4, 1998, Espoo, Finland, pp: 448-461.
CrossRef - Jakobsson, M., 1999. Flash mixing. Proceedings of the Eighteenth Annual ACM Symposium on Principles of Distributed Computing, May 4-6, 1999, Atlanta, Georgia, United States, pp: 83-89.
Direct Link - Jakobsson, M. and A. Juels, 2001. An optimally robust hybrid mix network. Proceedings of the 20th Annual ACM Symposium on Principles of Distributed Computing, August 26-28, 2001, Newport, Rhode Island, United States, pp: 284-292.
Direct Link - Jakobsson, M. and A. Juels, 2000. Mix and match: Secure function evaluation via ciphertexts. Proceedings of the 6th International Conference on the theory and Application of Cryptology and information Security: Advances in Cryptology, December 3-7, 2000, Springer-Verlag, London, pp: 162-177.
Direct Link - Jakobsson, M., K. Sako and R. Impagliazzo, 1996. Designated verifier proofs and their applications. Proceedings of the International Conference on the Theory and Application of Cryptographic Techniques, May 12-16, 1996, Saragossa, Spain, pp: 143-154.
CrossRef - Jonker, H.L. and E.P. De-Vink, 2006. Formalising receipt-freeness. Proceedings of the 9th International Conference on Information Security, August 30-September 2, 2006, Samos Island, Greece, pp: 476-488.
CrossRef - Juels, A., D. Catalano and M. Jakobsson, 2005. Coercion-resistant electronic elections. Proceedings of the 2005 ACM Workshop on Privacy in the Electronic Society, November 7, 2005, Alexandria, VA, USA., pp: 61-70.
Direct Link - Kancharla, P., K. Gummadidala and S. Saxen, 2007. Identity based strong designated verifier signature scheme. Informatica, 18: 239-252.
Direct Link - Kessler, V. and H. Neumann, 1998. A sound logic for analysing electronic commerce protocols. Proceedings of the 5th European Symposium on Research in Computer Security, September 16-18, 1998, London, UK., pp: 345-360.
Direct Link - Kiayias, A., M. Korman and D. Walluck, 2006. An internet voting system supporting user privacy. Proceedings of the 22nd Annual Computer Security Applications Conference, December 11-15, 2006, IEEE Computer Society, Washington, DC, pp: 165-174.
Direct Link - Klonowski, M., P. Kubiak and M. Kutyłowsk, 2008. Practical deniable encryption. Proceedings of the 34th Conference on Current Trends in Theory and Practice of Computer Science, January 19-25, 2008, Novy Smokovec, Slovakia, pp: 599-609.
CrossRef - Kremer, S. and M.D. Ryan, 2005. Analysis of an electronic voting protocol in the applied Pi calculus. Lect. Notes Comput. Sci., 3444: 186-200.
CrossRefDirect Link - Laguillaumie, F. and D. Vergnaud, 2004. Multi-Designated Verifiers Signatures. In: Information and Communi Cations Security, Lopez, J., S. Qing and E. Okamoto (Eds.). Springer-Verlag, Berlin Heidelberg, pp: 495-507.
CrossRef - Laguillaumie, F. and D. Vergnaud, 2005. Designated verifiers signature: Anonymity and efficient construction from any bilinear map. Proceedings of the 4th Conference on Security in Communication Networks, September 8-10, 2004, Springer-Verlag, pp: 107-121.
Direct Link - Laguillaumie, F., B. Libert and J.J. Quisquater, 2006. Universal Designated Verifier Signatures Without Random Oracles or Non-Black Box Assumptions. In: Security and Cryptography for Networks, De Prisco, R. and M. Yung (Eds.). Springer-Verlag, Berlin Heidelberg, pp: 63-77.
CrossRef - Lee, W.B., C.C. Wu and W.J. Tsaur, 2007. A novel deniable authentication protocol using generalized ElGamal signature scheme. Inform. Sci., 177: 1376-1381.
CrossRef - Lee, J.S. and J.H. Chang, 2006. Strong designated verifier proof signature without hash functions and the same scheme for an ad-hoc group ring. Int. J. Comput. Sci. Network Security, 6: 205-210.
Direct Link - Lei, C.L. and C.I. Fan, 1998. A universal single-authority election system. IEICE Trans. Fundam. Elect. Commun. Comput. Sci., E81-A: 2186-2193.
Direct Link - Lincoln, P., J. Mitchell, M. Mitchell and A. Scedrov, 1998. A probabilistic poly-time framework for protocol analysis. Proceedings of the 5th ACM Conference on Computer and Communications Security, November 2-5, 1998, San Francisco, California, United States, pp: 112-121.
Direct Link - Lu, R. and Z. Cao, 2005. A new deniable authentication protocol from bilinear pairings. Applied Math. Comput., 168: 954-961.
CrossRef - Lu, R. and Z. Cao, 2005. Non-interactive deniable authentication protocol based on factoring. Comput. Standards Interfaces, 27: 401-405.
CrossRef - Lynch, N., 1999. I/O automaton models and proofs for shared-key communication systems. Proceedings of the 12th Computer Security Foundations Workshop, June 28-30, 1999, Washington, DC., USA., pp: 14-29.
Direct Link - MacKenzie, P., T. Shrimpton and M. Jakobsson, 2002. Threshold password-authenticated key exchange. Proceedings of the 22nd International Annual Cryptology Conference on Advances in Cryptology, August 18-22, 2002, Springer-Verlag London, UK., pp: 385-400.
Direct Link - Magkos, E., M. Burmester and V. Chrissikopoulos, 2001. Receipt-freeness in large-scale elections without untappable channels. Proceedings of the IFIP Conference on Towards the E-Society: E-Commerce, E-Business, E-Government, October 3-5, 2001, Kluwer B.V., Deventer, The Netherlands, pp: 683-694.
Direct Link - Marneffe, O., O. Pereira and J.J. Quisquater, 2007. Simulation-Based Analysis of E2E Voting Systems. In: E-Voting and Identity, Alkassar, A. and M. Volkamer (Eds.). Springer Verlag, Berlin Heidelberg, pp: 137-149.
CrossRef - Mason, S., 2004. Is there a future for Internet voting? Comput. Fraud Security, 2004: 6-13.
CrossRefDirect Link - Mauw, S., J. Verschuren and E.P. De Vink, 2007. Data anonymity in the FOO voting scheme. Elect. Notes Theor. Comput. Sci., 168: 5-28.
CrossRefDirect Link - Meng, B., 2007. An internet voting protocol with receipt-free and coercion-resistant. Proceedings of the 7th International Conference on Computer and Information Technology, October 16-19, 2007, IEEE Computer Society, Washington DC, USA., pp: 721-726.
CrossRefDirect Link - Meng, B., 2007. Analysis of internet voting protocols with jonker-vink receipt freeness formal model. Proceedings of the International Conference on Convergence Information Technology, November 21-23, 2007, ICCIT., IEEE Computer Society, Washington, DC., pp: 663-669.
CrossRef - Meng, B., 2008. Formal analysis of key properties in the internet voting protocol using applied pi calculus. Inform. Technol. J., 7: 1133-1140.
CrossRefDirect Link - Meng, B., 2009. A secure non-interactive deniable authentication protocol with strong deniability based on discrete logarithm problem and its application on Internet voting protocol. Inform. Technol. J., 8: 302-309.
CrossRefDirect Link - Meng, B., 2009. A formal logic framework for receipt-freeness in internet voting protocol. J. Comput., 4: 184-192.
Direct Link - Michels, M. and P. Horster, 1996. Some remarks on a reciept-free and universally verifiable mix-type voting scheme. Proceedings of the International Conference on the Theory and Applications of Cryptology and Information Security: Advances in Cryptology, November 3-7, 1996, Springer-Verlag London, UK., pp: 125-132.
Direct Link - Mitchell, J.C., M. Mitchell and U. Stern, 1997. Automated analysis of cryptographic protocols using Mur. Proceedings of the 1997 Symposium on Security and Privacy, May 4-7, 1997, Digital Library, pp: 141.
Direct Link - Mitomo, M. and K. Kurosawa, 2000. Attack for Flash MIX. In: Advances in Cryptology-ASIACRYPT 2000, Okamoto, T. (Ed.). Springer-Verlag, Berlin Heidelberg, pp: 192-204.
CrossRef - Moran, T. and M. Naor, 2006. Receipt-Free Universally-Verifiable Voting with Everlasting Privacy. In: Advances in Cryptology-CRYPTO 2006, Dwork, C. (Ed.). Springer-Verlag, Berlin Heidelberg, pp: 373.
CrossRef - Neff, C.A., 2001. A verifiable secret shuffle and its application to e-voting. Proceedings of the 8th ACM Conference on Computer and Communications Security, November 5-8, 2001, Philadelphia, PA., USA., pp: 116-125.
Direct Link - Niemi, V. and A. Renvall, 1995. How to prevent buying of votes in computer elections. Proceedings of the 4th International Conference on the theory and Applications of Cryptology: Advances in Cryptology, November 28-December 1, 1995, Wollongong, Australia, pp: 164-170.
CrossRef - Nurmi, H. and A. Salomaa, 1998. A comparative overview ofcryptographic voting protocols. Ann. Operat. Res., 84: 29-43.
Direct Link - Okamoto, T., 1998. Receipt-Free Electronic Voting Schemes for Large Scale Elections. In: Security Protocols, Christianson, B., B. Crispo, T.M.A. Lomas and M. Roe (Eds.). Springer-Verlag, Berlin Heidelberg, pp: 25-35.
CrossRef - Ogata, W., K. Kurosawa, K. Sako and K. Takatani, 1997. Fault tolerant anonymous channel. Proceedings of the 1st International Conference on information and Communication Security, November 11-14, 1997, Springer-Verlag London, UK., pp: 440-444.
Direct Link - Paillier, P., 1999. Public-Key Cryptosystems Based on Composite Degree Residuosity Classes. In: Advances in Cryptology-EUROCRYPT '99, Stern, J. (Ed.). Springer-Verlag, Berlin Heidelberg, pp: 223-238.
CrossRef - Park, C., K. Itoh and K. Kurosawa, 1994. Efficient anonymous channel and all/nothing election scheme. Proceedings of the Workshop on the Theory and Application of Cryptographic Techniques on Advances in Cryptology, May 23-27, 1993, Lofthus, Norway, pp: 248-259.
Direct Link - Paulson, L.C., 1998. The inductive approach to verifying cryptographic protocols. J. Comput. Sec., 6: 85-128.
Direct Link - Pedersen, T.P., 1991. A Threshold Cryptosystem without a Trusted Party (Extended abstract). In: Advances in Cryptology-EUROCRYPT 91, Davies, D.W. (Ed.). Springer-Verlag, Berlin Heidelberg, pp: 522-526.
CrossRef - Pfitzmann, B. and A. Pfizmann, 1990. How to break the direct RSA-implementation of mixes. Proceedings of the Workshop on the Theory and Application of Cryptographic Techniques on Advances in Cryptology, April 10-13, 1989, Houthalen, Belgium, pp: 373-381.
Direct Link - Raimondo, M.D. and R. Gennaro, 2005. New approaches for deniable authentication. Proceedings of the 12th ACM Conference on Computer and Communications Security, November 7-11, 2005, ACM Press, New York, pp: 112-121.
CrossRefDirect Link - Rivest, R.L., S. Adi and T. Yael, 2001. How to Leak a Secret. Lecture Notes Comput. Sci., 2248: 552-565.
CrossRef - Sampigethaya, K. and R. Poovendran, 2006. A framework and taxonomy for comparison of electronic voting schemes. Comput. Security, 25: 136-153.
CrossRefDirect Link - Shao, Z., 2004. Efficient deniable authentication protocol based on generalized ElGamal signature scheme. Comput. Standards Interfaces, 26: 449-454.
CrossRef - Smith, W.D., 2005. New cryptographic voting scheme with best-known theoretical properties. Proceedings of the Workshop on Frontiers in Electronic Elections, September 2005, Milan, Italy, pp: 1-14.
Direct Link - Steinfeld, R., H. Wang and J. Pieprzyk, 2004. Efficient extension of standard schnorr/RSA signatures into universal designated-verifier signatures. Proceedings of the 7th International Workshop on Theory and Practice in Public Key Cryptography, Mar. 1-4, Singapore, pp: 86-100.
CrossRef - Susilo, W., F. Zhang and Y. Mu, 2004. Identity-Based Strong Designated Verifier Signature Schemes. In: Information Security and Privacy, Wang, H. at al. (Eds.). Springer-Verlag, Berlin Heidelberg, pp: 313-324.
CrossRef - Talbi, M., B. Morin, V. V.T. Tong, A. Bouhoula and M. Mejri, 2008. Specification of electronic voting protocol properties using ADM logic: FOO case study. Proceedings of the 10th international Conference on information and Communications Security, Oct. 20-22, Birmingham, UK., pp: 403-418.
Direct Link - Tatlı, E.I., D. Stegemann and S. Lucks, 2006. Dynamic mobile anonymity with mixing. Proceedings of the 7th International Workshop on Theory and Practice in Public Key Cryptography, March 1-4, 2006, Singapore, pp: 86-100.
CrossRef - Fabrega, F.J.T., J.C. Herzog and J.D. Guttman, 1998. Strand space: Why is a security protocol correct? Proceedings of the Symposium on Security and Privacy, May 3-6, 1998, ACM, USA., pp: 160-171.
CrossRef - Van Eijck, J. and S. Orzan, 2007. Epistemic verification of anonymity. Elect. Notes Theor. Comput. Sci., 168: 159-174.
CrossRefDirect Link - Weber, S.G., R. Araujo and J. Buchmann, 2007. On coercion-resistant electronic elections with linear work. Proceedings of the 2nd International Conference on Availability, Reliability and Security, April 10-13, 2007, IEEE Computer Society, Washington, DC, pp: 908-916.
CrossRef - Wei, H., Z. Dong and C. Ke-fei, 2007. A receipt-free punch-hole ballot electronic voting scheme. Proceedings of the 3rd International IEEE Conference on Signal-Image Technologies and internet-Based System December 16-18, 2007, IEEE Computer Society, Washington, DC, pp: 355-360.
CrossRef - Wikstrom, D., 2004. Five practical attacks for optimistic mixing for exit-polls. Proceedings of the 10th Annual International Workshop, Aug. 14-15, Ottawa, Canada, pp: 160-175.
CrossRef - Wikstrom, D., 2004. A Universally Composable Mix-Net. In: Theory of Cryptography, Maor, M. (Ed.). Springer Verlag, Berlin Heidelberg, pp: 317-335.
CrossRef - Wikstrom, D., 2005. A Sender Verifiable Mix-Net and a New Proof of a Shuffle. In: Advances in Cryptology-ASIACRYPT 2005, Roy, B. (Ed.). Springer Verlag, Berlin Heidelberg, pp: 273.
CrossRef - Wikstrom, D. and J. Groth, 2006. An Adaptively Secure Mix-Net without Erasures. In: Automata, Languages and Programming, Bugliesi, M. et al. (Eds.). Springer Verlag, Berlin Heidelberg, pp: 276-287.
CrossRef - Yao, A.C., 1982. Protocols for secure computations. Proceedings of the 23rd Annual Symposium on Foundations of Computer Science, Nov. 03-05, IEEE Computer Society, Washington, DC, pp: 160-164.
Direct Link - Yao, A.C., 1982. Theory and application of trapdoor functions. Proceedings of the 23rd Annual Symposium on Foundations of Computer Science, Nov. 3-5, IEEE Computer Society, Washington, DC., pp: 80-91.
Direct Link - Zhang, R., J. Furukawa and H. Imai, 2005. Short signature and universal designated verifer signature without random oracles. Proceedings of the 3rd International Conference Applied Cryptography and Network Security, Jun. 7-10, New York, USA., pp: 483-498.
CrossRef - Zhu, R.W., D.S. Wong and C.H. Lee, 2006. Cryptanalysis of a suite of deniable authentication protocols. IEEE Commun. Lett., 10: 504-506.
CrossRef - Zwierko, A. and Z. Kotulski, 2007. A light-weight e-voting system with distributed trust. Elect. Notes Theor. Comput. Sci., 168: 109-126.
CrossRefDirect Link - Karlof, C., N. Sastry and D. Wagner, 2005. Cryptographic voting protocols: A systems perspective. Proceedings of the 14th Conference on USENIX Security Symposium-Vol. 14, Baltimore, MD, Jul. 31-Aug. 05, USENIX Association, Berkeley, CA, pp: 1-17.
Direct Link - Ibrahim, M.H., 2009. Receiver-deniable public-key encryption. Int. J. Network Security, 8: 159-165.
Direct Link - Ibrahim, M.H., 2009. A method for obtaining deniable public-key encryption. Int. J. Network Security, 8: 1-9.
Direct Link - Meng, B., 2009. A secure internet voting protocol based on non-interactive deniable authentication protocol and proof protocol that two ciphertexts are encryption of the same plaintext. J. Networks, 4: 370-377.
CrossRefDirect Link - Chaum, D., 1998. Blind signatures for untraceable payments. Proceedings of the Advances in Cryptology, LNCS 1440, CRYPTO'82, Springer-Verlag, London, pp: 199-203.
Direct Link - Saeednia, S., S. Kremer and O. Markowitch, 2004. An Efficient Strong Designated Verifier Signature Scheme. In: Information Security and Cryptology-ICISC 2003, Lim, J.I. and D.H. Lee (Eds.). LNCS 2971, Springer-Verlag, Berlin, Heidelberg, ISBN: 978-3-540-21376-5, pp: 40-54.
CrossRefDirect Link








