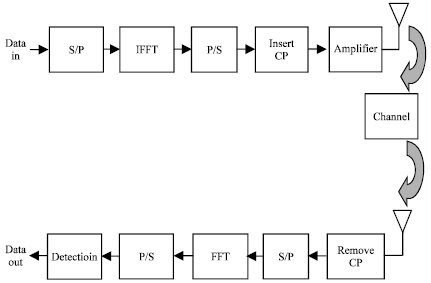
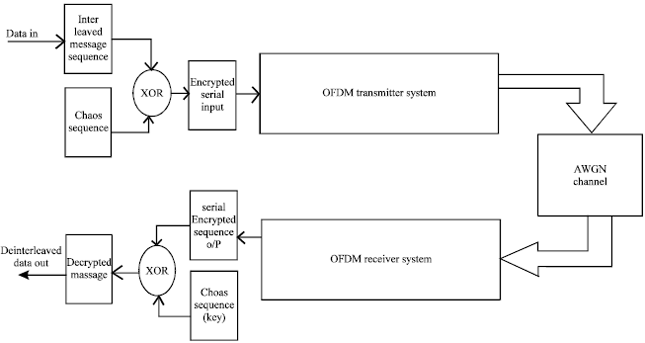
Research Article
Chaotic Interleaving for Secured OFDM
School of Electrical and Electronics Engineering, SASTRA University, Thanjavur, Tamil Nadu, India
B. Monisha
School of Electrical and Electronics Engineering, SASTRA University, Thanjavur, Tamil Nadu, India
R. Vishnupriya
School of Electrical and Electronics Engineering, SASTRA University, Thanjavur, Tamil Nadu, India
Niranjana Rangarajan
School of Electrical and Electronics Engineering, SASTRA University, Thanjavur, Tamil Nadu, India
G.N. Jayabhavani
School of Electrical and Electronics Engineering, SASTRA University, Thanjavur, Tamil Nadu, India
C. Nishanthini
School of Electrical and Electronics Engineering, SASTRA University, Thanjavur, Tamil Nadu, India