ABSTRACT
Orthogonal Frequency Division Multiplexing (OFDM) has come to the rescue of the bandwidth constraint owing to the burgeoning digital multimedia applications. The serial data is made parallel and transmitted over multiple orthogonal frequencies with bandwidth of each subcarrier considerably lesser than the coherence bandwidth of the channel. This study aims to review the present state of art in Error Correcting Codes (ECC) in OFDM, generated by methods like Convolutional Encoding, using Reed-Solomon Codes and Turbo codes. Furthermore the deployment of Artificial Neural Networks (ANN), to train the system for higher fault tolerance in OFDM is detailed.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2012.301.314
URL: https://scialert.net/abstract/?doi=jas.2012.301.314
INTRODUCTION
In Today’s multimedia communication scenario, a growing demand emerges for high-speed, reliable, high-quality digital data. These trends place significant challenges to the parallel data transmission scheme which alleviates the problems encountered with serial systems. High spectral efficiency and resilience to interference caused by multi-path effects are the fundamentals to meet the requirements of today’s wireless communication. The onset of Orthogonal Frequency Division Multiplexing (OFDM) has raised the wireless standards to 50 Mbps and higher, which creates a revolutionary in the wireless business. The first multichannel modulation systems transmitting binary data transmission over the SSB voice channel were implemented by Doelz et al. (1957). Multicarrier Modulation scheme was invented by Chang (1970) who proposed the orthogonality concept. Holsinger, (1964) determined the performance of fixed time continuous channel with memory and Inter-symbol interference. Saltzberg (1967) describes the effective parallel transmission, combating the effects of amplitude and delay distortion.
Zimmerman and Kirsch (1967) introduces the effective utilization of the spectrum with high data rate. Chang and Gibby (1968) presents a theoretical analysis on the performance of orthogonally multiplexed data transmission. FDM made more practical through DFT was proposed by Weinstein and Ebert (1971). The concept of frequency-domain data transmission by IDFT and DFT was described by Peled and Ruiz (1980). Cimini (1985) introduced OFDM in the wireless market place. Mathematical analysis of multipath radio propagation channel was described by Chung (1987). Bingham (1990) illustrates that Multicarrier Modulation (MCM) provides greater immunity towards noise and fades. High-speed wireless connectivity to the users accommodating COFDM in T-DAB and DFT based DMT have become the standard for ADSL (Akansu et al., 1998). Furthermore suitability of COFDM in telemedicine applications and multimedia data transmission is available in study of Thenmozhi and Prithiviraj (2008). The Space Time Frequency coded (STF) OFDM for broadband wireless communication systems is available in study of (Thenmozhi et al., 2011).
The increase in the symbol duration of OFDM Symbol for lower rate parallel streams and the relative decrease in the amount of dispersion in time caused by multipath delay spread has been explained in Bahai et al. (2004). Sending confidential information without affecting the regular OFDM operation is available in studies of Balaguru et al. (2010), Kumar et al. (2011) and Thenmozhi et al. (2011).
This study has taken a maiden effort to present a concise explanation on OFDM, A detailed description on Error Correcting Codes-namely, Convolutional Codes (CC), Reed-Solomon (RS) Codes and Turbo codes along with Artificial Neural Network (ANN) deployment in OFDM. To start with, an introduction to the OFDM system has been explained by Thenmozhi (2008). Followed by an OFDM performance and the associated problems are enumerated. Later, Various Error control codes are discussed. Penultimate Section addresses, how OFDM problems are coped with error control codes and neural networks. Finally, the concluding remarks are discussed in detail.
OFDM SYSTEM DESCRIPTION
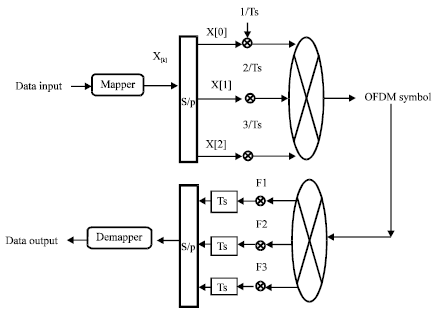
OFDM is a parallel transmission scheme where serial baseband high rate data bits are split into slow rate parallel data bits is shown in the Fig. 1. Willink and Wittke (1997) proposed that multicarrier transmission provides significant improvement in channel SNR. Since multiple carriers are used for transmission, the frequency selectivity of the wideband channel experienced by single-carrier transmission is overcome Casas and Leung (1991). The parallel data stream is modulated on different subcarriers making the subcarriers bandwidth very small when compared with the channel’s coherence bandwidth. The symbol period of the sub streams is made long compared to the delay spread of the channel.
They are then passed on to a signal mapper to produce N constellation data points depending on the modulation techniques used. It may be BPSK, QPSK or QAM. Kalet (1989) investigated multipath QAM provides better results than sigletone QAM. N is taken as an integer raised to the power of two, enabling the highly efficient FFT algorithms for modulation and demodulation. Then IFFT is used for modulating these data points on a set of orthogonal subcarriers (Arioua et al., 2012). N symbol is extended to NTs due to Serial to Parallel (S-P) conversion, so the length of the OFDM symbol Tsym = NTs.
Let the lth OFDM signal at kth subcarrier be denoted as ιl,k(t):
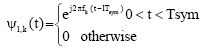 | (1) |
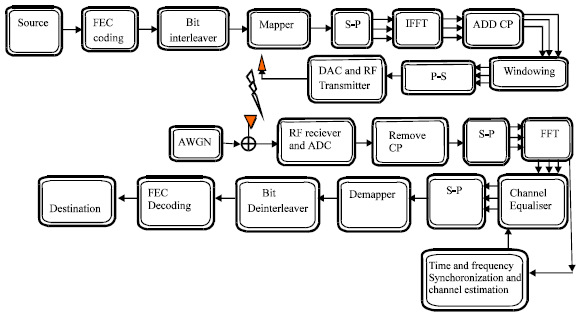
Discrete time OFDM symbol can be expressed as:
| (2) |
Received OFDM symbol is:
| (3) |
Xl(k ), the transmitted symbol can be reconstructed using orthogonality principle.
The subcarriers can be represented as complex exponential signals:
at fk = k/Tsym in OFDM signal where 0≤t≤Tsym.
 | |
| Fig. 1: | OFDM system model |
The subcarriers are said to be orthogonal if their integral product for their common period is zero:
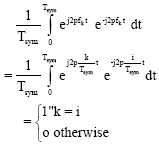 | (4) |
The output data will be in time domain. Guard Interval (GI) is introduced to preserve the orthogonality of the subcarriers (SCs) and is independent of subsequent OFDM symbols. The cyclic prefix which is transmitted during GI, copied the last part of OFDM symbol and pasted into the guard interval whose length should always exceed the maximum delay of the multipath channel as shown in Fig. 2. Elahmar et al. (2007) introduced a new algorithm in OFDM system called MERRY (Multicarrier Equalization by Restoration of Redundancy) which blindly and adaptively shorten the length of the channel to that of GI. The transmitted signal becomes periodic and the effect of the time-dispersive multipath channel becomes equivalent to a cyclic convolution, discarding the GI at the receiver. The GI is selected to have a length of one tenth to a quarter of the symbol period, leading to an SNR loss of 0.5 to 1 dB.
Orthogonality among six sinusoidal signals was taken which generated a matrix of signal vectors Xi in each row. To check the orthogonality, product of Xi and the transpose of Xi are taken and the results are shown in Fig. 3.
Complexity comparison between DFT and FFT computed by Hirosaki (1981) is summarized in Table 1.
Baseband OFDM can be expressed as:
| (5) |
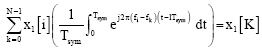 | (6) |
Multicarrier modulation at the transmitter and receiver can be implemented by using IFFT and FFT respectively and a sample for N = 3 is shown in Fig. 4 and the time domain representation is given in Fig. 5.
 | |
| Fig. 2: | OFDM symbol with cyclic prefix (CP) |
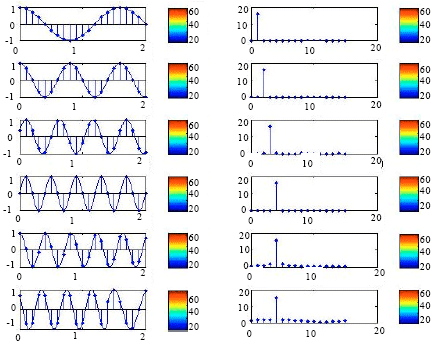 | |
| Fig. 3: | Orthogonality among subcarriers |
 | |
| Fig. 4: | Modulation and demodulation of OFDM with N = 3 |
 | |
| Fig. 5: | OFDM symbol |
| Table 1: | Summarized froms of the number of multiplications per output sample |
 | |
| M: Order of the high-rate FIR filter G(z), L: Number of sub bands, N: Baseband Data channels, A: The fractional part of f1/f0, f1: Frequency of the first channel, f0: Baud rate 1/T | |
| Table 2: | Parameters of OFDM |
 | |
The symbol demapper detects the data by an element wise multiplication of the FFT output by the inverse of the estimated channel frequency.
In the design of any OFDM receiver for physical layer IEEE802.11a (Thenmozhi et al., 2006), time and frequency synchronization are paramount to identify the start of the OFDM symbol and to align the local oscillator frequencies at the transmitter and receiver end . If there is any inaccuracy in any of the synchronization tasks, the orthogonality of the SCs is lost and this results in Intersymbol Interference (ISI) and Inter Carrier Interference (ICI). Jiang et al. (2010) simulated the joint proposal of Adaptive soft Frequency Reuse (AFR) and Maximum Ratio Combining (MRC) which mitigates ICI significantly.
Out of the 52 OFDM subcarriers, 4 are pilot subcarriers and remaining are for carrying Data with a carrier separation of 20/64 MHz = 0.3125 MHz. The subcarriers can be from BPSK, QPSK or QAM. The occupied bandwidth is around 16.6 MHz from the total 20 MHz Bandwidth which is given in Table 2. The symbol duration is 4 μsec including a guard interval of 0.8 μsec.
GI in OFDM symbols eliminates ISI caused by multipath propagation. It also eliminates the need of pulse-shaping filter and reduces time synchronization problems. When transmitted through Digital to analog converter, a high peak power signal is generated.
Windowing is a technique used to reduce side lobes of the received rectangular pulses thereby reducing the out of band transmitted signal. In OFDM, windowing must not influence the signal during its effective period. Kumar et al. (2008) have introduced time domain windowing scheme which considerably reduces ICI in comparison with the frequency domain techniques. Cyclic prefix and extended GI enhances the robustness of the delay spread. The orthogonality is preserved by implementing FFT at the receiver by gathering the knowledge about the OFDM symbol period and by knowing the start time of FFT. OFDM symbol is applied to the FFT to retrieve the data at the receiver. Channel estimation is required to retrieve the data contained in the signal constellation points. Liu et al. (2006) proposed a new algorithm called Quasi -Newton Acceleration (QNA) EM algorithm to perform channel estimation which reduces the complexity and the number of iterations, which enhances the BER. The receiver must have the phase reference to detect the data. Differential detection can also be used, which compares the phases of the symbol over adjacent subcarriers. OFDM best suits harsh multi-path environments. To maintain synchronization, OFDM includes several sub-carriers as pilot carriers that are used as phase reference for the synchronization of the receiver while demodulating data.
Frequency interleaving ensures the fading of the bit errors resulting from the subcarriers when part of the channel bandwidth. The faded subcarriers spread out rather than being concentrated. When travelling at high speed, time interleaving mitigates severe fading. Interleaving is used to distribute the errors randomly in the bit-stream.
Pros:
| • | Mitigates multipath |
| • | Resilience to interference |
| • | Spectrum efficiency |
Cons:
| • | High complexity and deployment costs |
| • | Guard bands reduce efficiency |
| • | Frequency offsets require accurate AFC |
| • | Synchronization is difficult |
| • | High peak-to-average power ratio |
Wire-line applications:
| • | VDSL and ADSL (very high bit rate Digital Subscriber Line Asymmetric Digital Subscriber Line) |
| • | MOCA (Multimedia over coax networking) |
| • | PLC (Power line communications) |
Wireless applications:
| • | IEEE 802.20 Mobile Broadband Wireless Access (MBWA) |
| • | IEEE 802.15.3a Ultra Wideband (UWB) Wireless PAN |
| • | Digital Video Broadcasting(DVB) |
| • | IEEE 802.11a, g, n (WiFi) Wireless LANs |
| • | Flash-OFDM cellular systems |
| • | 3GPP LTE (Long-Term Evolution) 4G mobile broadband standard downlink |
| • | IEEE 802.16 WiMAX (Worldwide Interoperability for Microwave Access) |
| • | IEEE 802.20 MBWA (Mobile Wireless MAN standard) |
| • | Digital Audio Broadcasting(DAB) |
| • | High Speed OFDM Packet Access (HSOPA) |
| • | Evolved UMTS Terrestrial Radio Access (E-UTRA) |
| • | IEEE 802.22 Wireless Regional Area Networks (WRAN) |
OFDM introduces three well-known tangles:
| • | High peak-to-average power ratio results in Nonlinear distortion at the power-amplification stage (Rappaport et al., 2002) |
| • | Vulnerability to synchronization errors |
| • | Sensitive to Doppler shift |
OFDM requires accurate synchronization of time and frequency between the transmitter and the receiver. The non ideal transmission conditions like imperfect channel estimation, symbol frame offset, carrier and sampling clock frequency offset, time-selective fading and critical analog components are analysed and the basic requirements for receiver synchronization are derived (Speth et al., 1999). If synchronization error is too large, then the orthogonality between the SCs are lost and the system SNR degrades resulting in ISI and ICI. Inter carrier interference also results from Doppler spreads or carrier phase jitters. OFDM consists of independently modulated subcarriers when added up produces large peak to average power ratio (Van Nee and Prasad, 2000). Thenmozhi et al. (2011) explained a detailed survey on OFDM, CDMA and how to combine them effectively called as MC CDMA for secure communication. Venkatesan and Ravichandran (2007) analysed the performance of MC CDMA systems and concluded that it’s the best multi access technique required by the 4G systems.
An efficient PAPR algorithm tries to reduce the BER to a minimum value (Wulich, 2005). Al-Kebsi (2008) introduced an algorithm by jointly combining Modulation adaptation, power control and clipping based on SER and SNR which provides maximum PAPR reduction (Latif and Gohar, 2008).
Doppler shift combined with Multipath results in reflections at various frequency and phase offsets and is very hard to compensate. Highly linear amplifiers are used for spectral spreading and distortion. Cimini et al. (1996) introduced clustered OFDM concept where the Peak Average Power is reduced even when subjected to non linearity’s.
ERROR CONTROL CODES
In Wireless communication, the input data are split up over parallel carriers resulting in nulls due to Multipath effects and selective fading. This results in few carrier bits to be received with error. These incorrect bits can be corrected by adding few bits to the transmitted data called the Error-correcting Code (ECC). The errors in degraded carriers are corrected with the information in the ECC, which doesn’t suffer from the same deep fade as the carrier and hence, the name Coded OFDM. Coding can be applied across several OFDM symbols (Zou and Wu, 1995). So, errors caused by symbols with a large degradation can be corrected by the surrounding symbols. Here, the error probability is no longer dependent on the power of individual symbols, but rather on the power of a number of consecutive symbols. Seddiki et al. (2006) evaluates BCH (Bose-Chaudhuri-Hocquenghem) codes over OFDM-BPSK modulation provides significant performance concentrating on some of the OFDM parameters.
Convolutional encoder: Convolutional encoder is a linear sequential circuit. The remarkable feature of the convolution encoder is that its output is a variable quantity making it very hard to crack. Input message bits are variable quantities and the operations take place between shift registers. Thus, the output changes to protect the information and thereby making the code hard to predict. Elias (1958) proposed the use of Convolutional codes for the discrete memory less channel. Then the general understanding of convolutional codes and sequential decoding was analysed by Viterbi (1967). The discussion and derivation of the backward version of the Viterbi decoding algorithm was carried out by Omura (1969). Forney (1970) structured various algebraic theorems on Convolutional codes. Furthermore the same author, Forney (1971) has constructed simple asymptotically optimum codes for bursty channel.
Viterbi decoder is a “maximum likelihood” technique provides greater improvement over the earlier complex methods (Akay and Ayanoglu, 2004). Convolutional encoding and Viterbi decoding (Forney, 1973) is an industry standard for all wireless channels. The concatenation of two convolutional encoders and an interleaver and a simple decoding algorithm revolutionized the coding field and their performances are very close to the Shannon theoretical capacity limits Benedetto (2004). Dos Santos et al. (2003) presented an insertion /deletion detection and correcting decoding scheme for convolutional codes based on the Viterbi decoding algorithm. Various concatenated Forward Error Correction (FEC) codes on the performance of a wireless Orthogonal Frequency Division are discussed by Haque et al. (2008) and Nyirongo et al. (2006).
Mercier et al. (2010) summarized error correcting codes for the channels that are perverted by synchronization errors and discussed its applications as well as the obstacles needed to overcome. Adnan and Masood (2011) made the comparison between uncoded and coded OFDM system and analysed the (SER) Symbol Error Rate as a function of Signal to Noise Ratio(SNR), with 1/2 rate convolution encoder and viterbi decoder has been analyzed and is shown in Fig. 6.
Convolutional encoder is specified by (n, k, m) where n denotes the output bits, k denotes the input bits and m denotes the memory registers (Seshadri and Sundberg, 1994). The measure of efficiency of the code is called as code rate k/n.
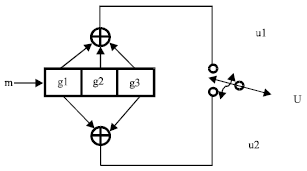 | |
| Fig. 6: | Convolutional encoder (2,1), m: Message input, u1: First code symbol, u2: Second code symbol, U: Output code word |
Constraint length L = k (m-1) specifies the bits in the encoder memory that influences the generation of output bits by adding superfluous bits:
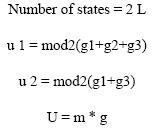 |
g-Generator polynomial which symbolizes the bit selection to be combined that contributes to the output bits (Blahut, 1985). Convolutional encoder will take single or multi-bit input and generates encoded outputs. Begin and Haccoun (1989) illustrates the various properties of convolutional codes. Noise and other factors in wireless channels alter the bit sequences. By introducing redundant bits, the original signal in presence of noise can be determined.
The most likely path of the transmitted sequence is computed by the Viterbi Algorithm using certain path metrics. Even in the presence of noise, the output will be the exact match of the input bits.
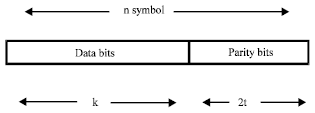
Reed Solomon (RS) codes: RS codes invented in 1960 by Reed and Solomon, RS (n, k ) is a systematic non binary cyclic block code and is represented in Fig. 7. These codes are based on Gaolis field where n = 2m -1 and k = 2m -1-2t (Blahut, 2002):
| • | n denotes the total symbols |
| • | k denotes the data symbols |
| • | t denotes the error correcting capability |
| • | For t = 2m -1, RS codes can correct “ t “ or “ n-k/2 “ symbols |
RS codes corrects a symbol with single bit error or even if all the bits in the symbol are in error. It is best suited for correcting burst errors produced by wireless channels. It is more sensitive to evenly spaced errors. RS codes are called as Maximum Distance separable codes and the minimum distance of an RS (n, k) code is n-k+1. Let g(x) = (x+α) (x+α2) (x+α2t ) where g(x)= g0 +g1(x2) + ….x2t
g(x) represents the generator polynomial. M(x)= m0(x) +m1(x) + …….
M(x) denotes the message bits. Then perform x2t m(x) / g(x)
x2t m(x) = a(x) g(x) + b(x) where b(x )= b0(x) + b1(x)+…… b(x) is the remainder and
b(x) + x2t m(x) is the codeword polynomial for the message.
Rs codes and Convolution codes are (Lee, 2005) the Coding schemes in IEEE802.16a OFDM and presented in Table 3.
Turbo codes: Berrrou et al. (1993) introduced a powerful new class of codes called Turbo codes which has been shown to perform near the Shannon capacity limit in an AWGN channel. Schlegel and Perez (2004) addresses turbo codes as parallel concatenated convolutional codes.
 | |
| Fig. 7: | RS code representation |
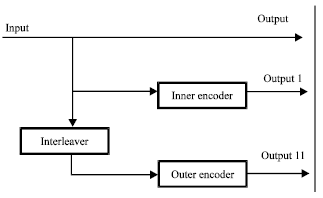 | |
| Fig. 8: | Representation of turbo code |
| Table 3: | Modulation and coding schemes in IEEE802.16a |
 | |
Wei (2004) and Hussain et al. (2011) proposed concatenation using block and convolutional codes with RS codes as the inner code and Convolutional codes as the outer code and they are the most preferred codes for data communications and digital TV systems and it’s diagrammatic representation is given in Fig. 8. Turbo codes are formed by the parallel concatenation of two identical encoders separated by an interleaver. Code word follows systematic form. The function of the interleaver is to scramble the data input in a Psuedo random fashion. Concatenated codes uses two levels of encoding one is the inner coding and other is the outer coding (Benedetto and Montorsi, 1996). The purpose of concatenated code is to achieve low probability of errors. The inner code is mostly connected with Modulators and channels to correct the channel errors and the outer codes reduces the error probability. Vafi et al. (2009) presents Serially Concatenated Turbo codes which is constructed as the serial combination of two turbo codes which outperform the parallel concatenated turbo codes. Performances of the commonly used trellis termination methods are compared and concluded that the performance depends on the choice of the interleaver Hokfelt et al. (1999). Afghah et al. (2008) proposes a new scheme of fast turbo codes which aims at space diversity and coding gain by utilizing turbo codes and Space time block codes as the inner and outer codes, respectively.
According to Lin et al. (1999), turbo codes is being considered to enhance mobile wireless channel performance. In a coded OFDM system with diversity to achieve high data rate has been explain by Muta and Akaiwa (2006), Salari et al. (2008) and Thenmozhi and Prithiviraj (2008). A similar approach on diversity reception but for CDMA in mobile application is available in study of Hemalatha et al. (2009).
NEURAL NETWORKS
Nowadays neural networks are gaining momentum for multiple applications. It mainly reduces long design analysis for the development of high-performance systems. These networks are self-organized mathematical learning models basing on domain knowledge and have the capability for modeling in the most of uncertainty and noise. It is pre-trained with several inputs and the error at the output is compared with the expected output for every session of training. Then the output layer is modified synchronously with the input layer, thereby reducing error rate and can be accomplished with lower complexity, faster convergence and offers superior BER performance capabilities when compared to the traditional means/schemes.
The artificial neuron was first introduced by McCullock and Pitts (1943). It is a network made up of interconnected processing elements called neurons. It has the ability to detect and extract complicated and imprecise data that cannot be handled by Computers and human beings. The artificial neurons learn by training to produce amazing results. Trained Neural network can be Adaptive; self organised, operates in real time applications and is Fault tolerant. The hypothesis of learning based on neural plasticity was proposed by Hebb (1949) and is popularly called as unsupervised Hebbian learning rule. Later, Farley and Clark (1954) simulated the Hebbian network using computational machines. For other neural networks, computational machines were made by Rochester et al. (1956).
Neural network model: Neural networks are made up of three layers namely input layer, hidden layer and output layer with full interconnections between them (Haykin, 1999). Input layer is passive and simply takes a single input and produces multiple outputs is shown in Fig. 9.
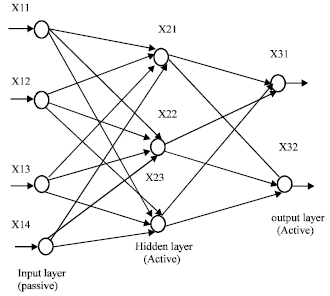 | |
| Fig. 9: | Neural network model |
Hidden and output layers are active, can modify the signal and take action based on the weights applied. A two layer perceptron learning algorithm for pattern recognition was created by Rosenblatt (1958). The mathematical computation of the Exor circuit could not be performed using the perceptron algorithm and was done through the back propagation algorithm by Werbos (1974). Neural networks are more adaptive systems that transform a vector from input to the corresponding vector at the output. The neurons are characterized by internal threshold and by the type of activation function. To accomplish desired mapping, the network should iterate with a change in its internal parameters called the training process, until a set of parameters is found which minimizes the error between the computed and the desired output vector.
PAPR reduction techniques with neural networks: PAPR results in high out-of-band emission called spectrum spreading and non linear distortion.
Van Nee and Prasad (2000) which is mainly due to the large number of subcarriers in OFDM. Several PAPR reduction schemes have been proposed. Signal distortion techniques (Li and Cimini, 1997) like clipping, peak windowing and peak cancellation which reduce the peak amplitudes by nonlinearly distorting the OFDM signal around the peak values have been analysed by Van Nee and Prasad (2000) and Wang et al. (1999). A prominent solution to reduce PAPR is by utilizing coding techniques is given by Van Nee and Prasad (2000), Larsen et al. (2004) and Paterson and Tarokh (2000) which improves the bit error rate. The fluctuations are given by PAPR = max p(t)/Pav where p(t) and pav represents the instantaneous and average power of one OFDM symbol.
According to Davis and Jedwab (1999), Selective Mapping (SLM) the transmit sequence is multiplied by the random sequence which is selected to minimize PAPR of OFDM signal (Wilkinson and Jones, 1995). In Partial transmit sequence (Hagenauer et al., 1996; Pundiah, 1998) PAPR of the OFDM signal is reduced by grouping all subcarriers into several clusters and adjusting the phase of each cluster, symbol-by-symbol, to minimize the PAPR (Tarokh and Jafarkhani, 2000). Latif and Gohar (2008) used a Hybrid QAM-FSK OFDM transceiver which produces a reduction in PAPR compared to Partial transmit sequence method of PAPR scheme by Latif and Gohar (2003). Hassan and El-Tarhuni (2011) made a comparative study between SLM, modified SLM and PTS. All the techniques provide improvement in PAPR reduction. As the phase sequences increases, the PAPR reduction increases in the expense of complexity. Modified SLM outperforms the conventional SLM. SLM has an improvement of 0.5 dB in PAPR reduction than that of PTS scheme.
PAPR reduction techniques with convolutional codes: Wang et al. (2008) and Khan and Sheikh (2009) discuss in detail to reduce PAPR in OFDM system, by employing SLM technique with Convolutional codes and avoids the transmission of side information. PAPR reduction using Convolutional coding employing PTS method is discussed (Verma et al., 2011). 8-ASK mapping based on SLM is presented and the results show reduction in PAPR (Sichao and Dongfeng, 2005). Standard convolution code (7, [171,133]) used in wireless systems is used and provides reasonably good BER and PAPR reduction compared to other non-identical polynomial codes (Vallavaraj et al., 2006). Terminated convolutional codes with offset for PAPR reduction is given by Chen et al. (2003). The convolutional codes which can be easily decoded by using the Viterbi algorithm, have low PAPR and acceptable code rates. The peak to average power ratio of convolutional coded OFDM signals can be significantly degraded when compared with uncoded-OFDM. This degradation occurs for code rates R<1/2 and relatively low constraint lengths (Frontana and Fair, 2007).
PAPR reduction techniques with TURBO CODES: Muta and Akaiwa (2006) entails an exhaustive search for low PAPR in OFDM and proposes a weighting factor method. In this method, without using any side information turbo codes are capable of error correction and also estimating the weighting function. They extended their estimation using PTS in (Muta and Akaiwa, 2008). Sabbaghian et al. (2011) propose of a time-frequency turbo block code to achieve better BER with a low PAPR close to the Shannon limit. Tsai and Ueng, (2007) has given a way to achieve low PAPR and higher BER, authors employs tail-biting turbo code to generate multiple candidates using SLM which results in RS codes similar to the conventional one excluding 1,2 of RS codes in tail-bit form. The tail-biting codeword starts and ends in the same state. To mitigate peak power problem in OFDM three turbo code OFDM systems are introduced by Lin et al. (2003). In the first method short codes are used to protect the side information and long maximum length sequences are used as test sequences. This results in protection of the side information by increasing the power of subcarriers. In the Second method, no side information is required. It employs various interweavers to produce output with various PAPR and selects the one with the lowest PAPR. The third method employs the combination of one and two and method three has better BER performance and higher transmission rate and LOW PAPR .
PAPR reduction techniques with RS codes: In contrast to the existing approaches to reduce PAPR in OFDM, RS codes and simplex codes are arranged over the frames of OFDM and pick out the best one which provides low PAPR (Fischer and Siegl, 2009). RS-OFDM is analysed over Rayleigh fading channels with Additive White Gaussian Noise (AWGN). It is the combination of Reed-Solomon (RS) codes and Orthogonal Frequency Division Multiplexing (OFDM), in which RS code operates as the OFDM front-end. Van Meerbergen et al. (2006a) provides low Peak to Average Power Ratio (PAPR) and removes ISI by Gaolis field equalizer. It also provides better results compared to traditional coded OFDM. Van Meerbergen et al. (2006b) and Fischer and Siegl (2008) presents a new design solution for low PAPR in presence of impulse noise. The problem is tackled by decomposing the circular channel matrix into parallel channels by using DFT matrices in a Galois field of odd characteristic, rather than in a complex field. OFDM merged with a Reed-Solomon (RS) code, with its maximal Hamming distance is preferred for impulse noise cancellation.
OFDM USING NEURAL NETWORKS
OFDM pulse shape generation using ANN is discussed by Akah et al. (2009). Necmi and Nuri (2010) uses Multilayered Perceptrons (MLP) with Back Propagation (BP) learning algorithm as a channel estimator for OFDM systems. A comparison between neural based channel estimator with Least Square (LS) algorithm, Minimum mean Square Error (MMSE) algorithm and Radial Basis Function neural network (RBF) was analysed with respect to Bit Error Rate (BER) and Mean Square Error (MSE). From the analysis MLP neural network has better performance than the others and provides better channel estimation. Multilayered Perceptrons (MLP) based ACE (Active Constellation Expansion) to reduce fluctuations in power envelope of OFDM signal was studied (Jabrane et al., 2010). Charalabopoulos et al. (2003) proposed a Radial Basis Function (RBF) neural network which are used to provide channel equalization to combat the frequency selective fading in OFDM systems. Mizutani et al. (2007) uses Hopfield neural network and Back propagation Neural networks in order to provide reduction in PAPR without the necessity of the side information required in other systems. According to Chen et al. (2007), equalizer is built using Back propagation algorithm and learning of the network is done through MLP method which outperforms than the conventional equalizer. Learning of neural network is done through MLP and the equalizer is based on Back Propagation algorithm and yields better performance than the conventional equalizer. Louet et al. (2004) used neural networks to compensate the non-linear effects in OFDM created by high power amplifiers and thus eliminates the peak factor problem. Fischer and Siegl (2009), focuses on the Maximum Distance separable code property of RS codes to achieve reduction in PAPR. Wang et al. (2004) compares PAPR and carrier frequency offset between OFDM and single-carrier system with zero padding and justified that ZP is preferred when code rate is high and OFDM is preferred for lower code rates. According to Pei et al. (2010), concentrates on the resource allocation for OFDM based system considering mutual interference using the Genetic algorithm approach.
CONCLUSION
OFDM is thus used to overcome the bandwidth constraint and provide better SNR. Its implementation and the problems associated with it are explained in detail. Pros and cons of OFDM and its wire-line, wireless applications have been listed. Three types of error correcting codes called Convolutional codes, RS codes and Turbo codes have been illustrated with necessary theory and enumerated its weakness. It is also discussed as to how these problems can be overcome by the use of error control codes and neural networks. The various error code generation techniques have been explained. A detailed survey has been carried out to on PAPR reduction techniques using Neural Networks and Error Correcting Codes.
REFERENCES
- Adnan, T. and A. Masood, 2011. Use of convolution coding for improving SER performance of OFDM system. Proceedings of the 3rd IEEE International Conference on Communication Software and Networks, May 27-29, 2011, School of Electronic Engineering University of New South Wales, Sydney, NSW, Australia, pp: 40-43.
CrossRefDirect Link - Akay, E. and E. Ayanoglu, 2004. High performance Viterbi decoder for OFDM systems. Proc. IEEE Vehicular Technol. Conf., 1: 323-327.
CrossRef - Akansu, A.N., P. Duhamel, X.M. Lin and M. de Courville, 1998. Orthogonal transmultiplexers in communication: A review. IEEE Trans. Signal. Process., 46: 979-995.
CrossRefDirect Link - Akah, H.M., A. Kamel and H.M. El-Hennawy, 2009. OFDM pulse shape generation using artificial neural networks. Proceedings of the IEEE EUROCON, May 18-23, 2009, Natiional Authority of Remote Sensing and Space Science, Cairo, Egypt, pp: 1694-1699.
CrossRef - Amirtharajan, R., K. Thenmozhi and R.J.B. Balaguru, 2010. Multi carrier steg against omni attacks. Int. J. Comput. Applic., 5: 35-40.
Direct Link - Arioua, M., S. Belkouch and M.M. Hassani, 2012. Efficient 16-points FFT/IFFT architecture for OFDM based wireless broadband communication. Inf. Technol. J., 11: 118-125.
CrossRefDirect Link - Latif, A. and N.D. Gohar, 2008. On the PAPR reduction properties of hybrid QAM-FSK (HQFM) OFDM transceiver. J. Applied Sci., 8: 1061-1066.
CrossRefDirect Link - Blahut, R.E., 1985. Algebraic fields, signal processing and error control. Proc. IEEE, 73: 874-893.
CrossRefDirect Link - Begin, G. and D. Haccoun, 1989. High-rate punctured convolutional codes: Structure properties and construction technique. IEEE Trans. Commun., 37: 1381-1385.
CrossRefDirect Link - Benedetto, S. and G. Montorsi, 1996. Unveiling turbo codes: Some results on parallel concatenated coding schemes. IEEE Trans. Inform. Theory, 42: 409-428.
CrossRefDirect Link - Berrrou, C., A. Glavieux and O. Thitimajshima, 1993. Near Shannon limit error-correcting coding and decoding: Turbo-codes. Proceedings of the IEEE International Conference on Communication, May 23-26, 1993, Geneva, Switzerland, pp: 1064-1070.
CrossRef - Bingham, J.A.C., 1990. Multicarrier modulation for data transmission. An idea whose time has come. IEEE Commun. Mage., 28: 5-14.
CrossRefDirect Link - Chang, R. and R. Gibby, 1968. A theoretical study of performance of an orthogonal multiplexing data transmission scheme. IEEE Trans. Commun. Technol., 16: 529-540.
CrossRefDirect Link - Casas, E.F. and C. Leung, 1991. OFDM for data communication over mobile radio FM channels. I. Analysis and experimental results. IEEE Trans. Commun., 39: 783-793.
CrossRefDirect Link - Cimini, L.J., 1985. Analysis and simulation of a digital mobile channel using orthogonal frequency division multiplexing. IEEE Trans. Commun., 33: 665-675.
CrossRefDirect Link - Cimini Jr., L.J., B. Daneshrad and N.R. Sollenberger, 1996. Clustered OFDM with transmitter diversity and coding. IEEE Global Telecommun. Conf., 1: 703-707.
CrossRef - Charalabopoulos, G., P. Stavroulakis and A.H. Aghvami, 2003. A frequency-domain neural network equalizer for OFDM. IEEE Global Telecommun. Conf., 2: 571-575.
CrossRefDirect Link - Chung, J.C., 1987. The effect of time delay spread on portable radio communications channels with digital modulation. IEEE J. Selected Areas Commun., 5: 879-889.
Direct Link - Davis, J.A. and J. Jedwab, 1999. Peak-to-mean power control in OFDM, Golay complementary sequences and Reed-Muller codes. IEEE Trans. Inform. Theory, 45: 2397-2417.
CrossRefDirect Link - Doelz, M.L., E.T. Heald and D.L. Martin, 1957. Binary data transmission techniques for linear systems. Proc. IRE, 45: 656-661.
CrossRefDirect Link - Dos Santos, M.P.F., W.A. Clarke, H.C. Ferreira and T.G. Swart, 2003. Correction of insertions/deletions using standard convolutional codes and the Viterbi decoding algorithm. Proceedings of the IEEE workshop on Information Theory, March 31-April 4, 2003, Rand Afrikaans University, South Africa, pp: 187-190.
- Elahmar, S., A. Djebbari, M. Bouziani and J.M. Rouvaen, 2007. New results with blind time domain equalization for OFDM system. Inform. Technol. J., 6: 207-211.
CrossRefDirect Link - Elias, P., 1958. Computation in the presence of noise. IBM J. Res. Dev., 2: 346-353.
CrossRefDirect Link - Farley, B. and W. Clark, 1954. Simulation of self-organizing systems by digital computer. IRE Trans. Inform. Theory, 4: 76-84.
CrossRefDirect Link - Afghah, F., M. Ardebilipour and A. Razi, 2008. Fast turbo codes concatenated with space-time block codes. J. Applied Sci., 8: 2867-2873.
CrossRefDirect Link - Fischer, R.F.H. and C. Siegl, 2008. Peak-to-average power ratio reduction in OFDM using reed-solomon codes. Proceedings of the IEEE International Zurich Seminar on Communications, March 12-14, 2008, Zurich, Switzerland, pp: 40-43.
CrossRef - Fischer, R.F.H. and C. Siegl, 2009. Reed-solomon and simplex codes for peak-to-average power ratio reduction in OFDM. IEEE Trans. Inform. Theory, 55: 1519-1528.
CrossRef - Forney, Jr. G.D., 1970. Convolutional codes I: Algebraic structure. IEEE Trans. Inform. Theory, 16: 720-738.
CrossRef - Forney, Jr. G.D., 1971. Burst-correcting codes for the classic bursty channel. IEEE Trans. Commun. Technol., 19: 772-781.
CrossRef - Frontana, E. and I. Fair, 2007. Avoiding PAPR degradation in convolutional coded OFDM signals. Proceedings of the IEEE Pacific Rim Conference on Communications, Computers and Signal Processing, August 22-24, 2007, Victoria, Canada, pp: 312-315.
CrossRef - Hussain, G.A., M.B. Mokhtar and R.S.A.B. Raja, 2011. Concatenated RS-convolutional codes for MIMO-OFDM system. Asian J. Applied Sci., 4: 720-727.
CrossRefDirect Link - Hassan, Y. and M. El-Tarhuni, 2011. A comparison of SLM and PTS peak-to-average power ratio reduction schemes for OFDM systems. Proceedings of the 4th International Conference on Modeling, Simulation and Applied Optimization, April 19-21, 2011, Kuala Lumpur, Malaysia, pp: 1-4.
CrossRef - Hagenauer, J., E. Offer and L. Papke, 1996. Iterative decoding of binary block and convolutional codes. IEEE Trans. Inform. Theory, 42: 429-445.
CrossRef - Liu, H., H. Zhong, T. Zhang and Z. Gong, 2006. A quasi-newton acceleration EM algorithm for OFDM systems channel estimation. Inf. Technol. J., 5: 749-752.
CrossRef - Haque, M.D., S.E. Ullah and M.R. Ahmed, 2008. Performance evaluation of a wireless orthogonal frequency division multiplexing system under various concatenated FEC channel-coding schemes. Proceedings of the 11th International Conference on Computer and Information Technology, December, 24-27, 2008, Bangladesh, pp: 94-97.
- Hebb, D.O., 1949. The Organization of Behavior:A Neuropsychological Theory. 1st Edn., Wiley, New York, ISBN: 0805843000.
Direct Link - Hemalatha, M., K. Thenmozhi, V. Prithiviraj, D. Bharadwaj and R. Vignesh, 2009. Diversity reception for CDMA based mobile communication systems. Proceedings of the 1st International Conference on Wireless Communication, Vehicular Technology, Information Theory and Aerospace and Electronic Systems Technology, May 17-20, 2009, Aalborg, pp: 660-664.
CrossRef - Hirosaki, B., 1981. An orthogonally multiplexed QAM system using the discrete fourier transform. IEEE Trans. Commun., 29: 982-989.
Direct Link - Hokfelt, J., O. Edfors and T. Maseng, 1999. A survey on trellis termination alternatives for turbo codes. IEEE Veh. Technol. Conf., 323: 2225-2229.
CrossRef - Al-Kebsi, I.I.M., 2008. The impact of modulation adaptation and power control on peak to average power ratio clipping technique in orthogonal frequency division multiplexing of fourth generation systems. J. Applied Sci., 8: 2776-2780.
CrossRefDirect Link - Jabrane, Y., V.P.G. Jimenez, A.G. Armada, B.A.E. Said and A.A. Ouahman, 2010. Reduction of power envelope fluctuations in OFDM signals by using neural networks. IEEE Commun. Lett., 14: 599-601.
CrossRef - Khan, K. and S.A. Sheikh, 2009. PAPR reduction of OFDM signals using convolutional codes. Proceedings of the IEEE Student Conference on Research and Development, November 16-18, 2009, UPM, Serdang, Malaysia, pp: 26-28.
CrossRef - Kumar, R., S. Malarvizhi and S. Jayashri, 2008. Time-domain equalization technique for intercarrier interference suppression in OFDM systems. Inform. Technol. J., 7: 149-154.
CrossRefDirect Link - Kumar, P.P., R. Amirtharajan, K. Thenmozhi and J.B.B. Rayappan, 2011. Steg-OFDM blend for highly secure multi-user communication. Proceedings of the 2nd International Conference on Vehicular Technology, Information Theory and Aerospace and Electronic Systems Technology, February 28-March 3, 2011, Chennai, India, pp: 1-5.
CrossRef - Wei, L., 2004. Iterative Viterbi algorithm: implementation issues. IEEE Trans. Wireless Commun., 3: 382-386.
CrossRefDirect Link - Louet, Y., S. Tertois and P. Barreau, 2004. Reducing nonlinear OFDM signal distortions using neural networks in the time domain. Proceedings of the Internation. Conf. on Information and Communication Technologies, From Theory to Applications, April 19-23, 2004, Omayyad Palace, Damascus, pp: 267-268.
CrossRef - Larsen, Y., G. Leus and G.B. Giannakis, 2004. Constant modulus and reduced PAPR block differential encoding for frequency-selective channels. IEEE Trans. Commun., 52: 622-631.
CrossRef - Lin, L., L.J. Cimini and J.C.I. Chuang, 1999. Turbo codes for OFDM with antenna diversity. IEEE Veh. Technol. Conf., 2: 1664-1668.
CrossRef - Sichao, L. and Y. Dongfeng, 2005. Reducing PAPR of OFDM with convolutional code and 8-ask mapping. Proceedings of the International Conference on Wireless Communications, Networking and Mobile Computing, September 23-26, 2005, China, pp: 253-256.
CrossRef - Lin, M.C., K.C. Chen and S.L. Li, 2003. Turbo coded OFDM system with peak power reduction. IEEE Veh. Technol. Conf., 4: 2282-2286.
CrossRef - Mercier, H., V.K. Bhargava and V. Tarokh, 2010. A survey of error-correcting codes for channels with symbol synchronization errors. IEEE Commun. Surv. Tutorials, 12: 87-96.
CrossRef - Mizutani, K., M. Ohta, Y. Ueda and K. Yamashita, 2007. A PAPR reduction of OFDM signal using neural networks with tone injection scheme. Proceedings of the 6th International Conference on Information, Communications and Signal Processing, December 10-13, 2007, Singapore, pp: 1-5.
CrossRef - Muta, O. and Y. Akaiwa, 2006. A weighting factor estimation scheme for phase-control based peak power reduction of turbo-coded OFDM signal. Proceedings of the IEEE Vehicular Technology Conference, May 7-10, 2006, Melbourne, pp: 1477-1481.
CrossRef - Muta, O. and Y. Akaiwa, 2008. Iterative weighting factor estimation method for peak power reduction with adaptive subcarrier-phase control in turbo-coded multi-carrier CDM Systems. Proceedings of the IEEE 68th Vehicular Technology Conference, September 21-24, 2008, Calgary, pp: 1-5.
CrossRef - Nyirongo, N., W.Q. Malik and D.J. Edwards, 2006. Concatenated RS-convolutional codes for ultrawideband multiband-OFDM. Proceedings of the IEEE International Conference on Ultra-Wideband, September 24-27, 2006, Waltham, MA., USA., pp: 137-142.
CrossRef - Omura, J., 1969. On the Viterbi decoding algorithm. IEEE Trans. Inform. Theory, 15: 177-179.
CrossRef - Paterson, K.G. and V. Tarokh, 2000. On the existence and construction of good codes with low peak-to-average power ratios. Proceedings of the IEEE International Symposium on Information Theory, June 25-30, 2000, Sorrento, pp: 217.
CrossRef - Peled, A. and A. Ruiz, 1980. Frequency domain data transmission using reduced computational complexity algorithms. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, April 19-24, 1980, Taipei, Taiwan, pp: 964-967.
CrossRef - Venkatesan, G.K.D.P. and V.C. Ravichandran, 2007. Performance analysis of MC-CDMA for wide band channels. Inform. Technol. J., 6: 267-270.
CrossRefDirect Link - Pundiah, R.M., 1998. Near optimum decoding of product codes. IEEE Trans. Comm., 4: 1003-1010.
CrossRefDirect Link - Rappaport, T.S., A. Annamalai, R.M. Buehrer and W.H. Tranter, 2002. Wireless communications: Past events and a future perspective. IEEE Commun. Maga., 40: 148-161.
CrossRefDirect Link - Rochester, N., J. Holland, L. Habit and W. Duda, 1956. Tests on a cell assembly theory of the action of the brain, using a large digital computer. IRE Transact. Inf. Theory, 2: 80-93.
CrossRef - Rosenblatt, F., 1958. The perceptron: A probabilistic model for information storage and organization in the brain. Psych. Rev., 65: 386-408.
CrossRefPubMedDirect Link - Sabbaghian, M., Y. Kwak, B. Smida and V. Tarokh, 2011. Near shannon limit and low peak to average power ratio turbo block coded OFDM. IEEE Trans. Commun., 59: 2042-2045.
CrossRef - Salari, S., M. Ardebilipour and M. Ahmadian, 2008. Channel and frequency offset estimation for MIMO-OFDM systems. J. Applied Sci., 8: 809-815.
CrossRefDirect Link - Saltzberg, B., 1967. Performance of an efficient parallel data transmission system. IEEE Trans. Commun. Technol., 15: 805-811.
CrossRefDirect Link - Seddiki, A., A. Djebbari, J.M. Rouvaen and A. Taleb-Ahmed, 2006. BCH coding performance evaluation on a land mobile channel based OFDM system. Inform. Technol. J., 5: 930-936.
CrossRefDirect Link - Seshadri, N. and C.E.W. Sundberg, 1994. List Viterbi decoding algorithms with applications. IEEE Trans. Commun., 42: 313-323.
CrossRef - Lee, S.G., 2005. Performance of concatenated FEC under fading channel in wireless-MAN OFDM system. Proc. 19th Int. Conf. Adv. Inf. Network. Applic., 1: 781-785.
CrossRefDirect Link - Speth, M., S.A. Fechtel, G. Fock and H. Meyr, 1999. Optimum receiver design for wireless broad-band systems using OFDM. I. IEEE Trans. Commun., 47: 1668-1677.
CrossRefDirect Link - Tarokh, V. and H. Jafarkhani, 2000. On the computation and reduction of the peak-to-average power ratio in multicarrier communications. IEEE Trans. Commun., 48: 37-44.
CrossRefDirect Link - Necmi, T. and S.M. Nuri, 2010. Back propagation neural network approach for channel estimation in OFDM system. Proceedings of the IEEE International Conference on Wireless Communications, Networking and Information Security, June 25-27, 2010, Beijing, China, pp: 265-268.
CrossRef - Thenmozhi, K., V.K. Konakalla, S.P.P. Vabbilisetty and R. Amirtharajan, 2011. Space Time Frequency coded (STF) OFDM for broadband wireless communication systems. J. Theor. Applied Inform. Technol., 3: 53-59.
Direct Link - Thenmozhi, K. and V. Prithiviraj, 2008. Suitability of Coded Orthogonal Frequency Division Multiplexing (COFDM) for multimedia data transmission in wireless telemedicine applications. Conf. Comput. Intelli. Multimedia Appl., 4: 288-292.
CrossRef - Vallavaraj, A., G.S. Brian, K.H. David and G.M. Francis, 2006. Optimizing the rate 1/2; convolutional code for OFDM applications in terms of bit-error-rate and peak-to-average power ratio. Proceedings of the IEEE GCC Confrrence, March 20-22, 2006, Manama, pp: 1-6.
CrossRef - Vafi, S., T. Wysocki and M. Abolhasan, 2009. Serially concatenated turbo codes. Proceedings of the 5th International Conference on Wireless Communications, Networking and Mobile Computing, September 24-26, 2009, Beijing, China, pp: 1-4.
CrossRef - Van Meerbergen, G., M. Moonen and M. De Man, 2006. Reed-solomon codes implementing a coded OFDM scheme for rayleigh fading channels. Proceedings of the Global Telecommunications Conference IEEE, Nov. 27- Dec. 1, San Francisco, CA, pp: 1-6.
CrossRef - Verma, S., P. Sharma, S. Ahuja and P. Hajela, 2011. Partial transmit sequence with convolutional codes for reducing the PAPR of the OFDM signal. Proceedings of the 3rd International Conference Electronics Computer Technology, April 8-10, 2011, Kanyakumari, pp: 70-73.
CrossRef - Viterbi, A., 1967. Error bounds for convolutional codes and an asymptotically optimum decoding algorithm. IEEE Trans. Inform. Theor., 13: 260-269.
Direct Link - Weinstein, S. and P. Ebert, 1971. Data transmission by frequency-division multiplexing using the discrete fourier transform. IEEE. Trans. Commun., 19: 628-634.
CrossRefDirect Link - Jiang, W., Z. Zhang, Y. Xu and L. Sun, 2010. Dynamic inter-cell interference cancellation for uplink in multi-cell OFDMA systems. Inform. Technol. J., 9: 1490-1494.
CrossRefDirect Link - Wilkinson, T.A. and A.E. Jones, 1995. Minimisation of the peak to mean envelope power ratio of multicarrier transmission schemes by block coding. Vehicular Technol. Conf., 2: 825-829.
CrossRef - Willink, T.J. and P.H. Wittke, 1997. Optimization and performance evaluation of multicarrier transmission. IEEE Trans. Infor. Theory, 43: 426-440.
CrossRefDirect Link - Wulich, D., 2005. Definition of efficient PAPR in OFDM. IEEE Commun. Lett., 9: 832-834.
CrossRefDirect Link - Wang, X., T.T. Tjhung and C.S. Ng, 1999. Reduction of peak-to-average power ratio of OFDM system using a companding technique. IEEE Trans. Broadcast., 45: 303-307.
CrossRefDirect Link - Tsai, Y.C. and Y.L. Ueng, 2007. A tail-biting turbo coded OFDM system for PAPR and BER reduction. Proceedings of the 66th Vehicular Technology Conference, September 30-October 3, 2007, Baltimore, pp: 1067-1071.
CrossRefDirect Link - Zimmerman, M. and A. Kirsch, 1967. The AN/GSC-10 (KATHRYN) variable rate data modem for HF radio. IEEE Trans. Commun. Technol., 15: 197-204.
CrossRefDirect Link - Wang, Z., X. Ma and G.B. Giannakis, 2004. OFDM or single-carrier block transmissions. IEEE Trans. Commun., 52: 380-394.
CrossRefDirect Link - Li, X. and L.J. Cimini, 1997. Effects of clipping and filtering on the performance of OFDM. Proceedings of the IEEE 47th Vehicular Technology Conference, May 4-5, Phoenix, AZ. USA., pp: 1634-1638.
CrossRef - McCulloch, W.S. and W. Pitts, 1943. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys., 5: 115-133.
CrossRefDirect Link - Pei-Pei, C., Z. Qin-Yu, W. Ye and M. Jing, 2010. Multi-objective resource allocation for OFDM-based cognitive radio systems. Inform. Technol. J., 9: 494-499.
CrossRefDirect Link








