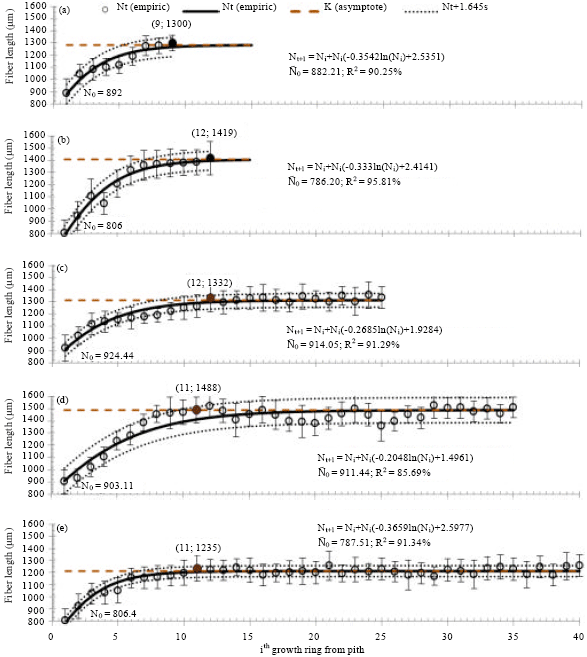
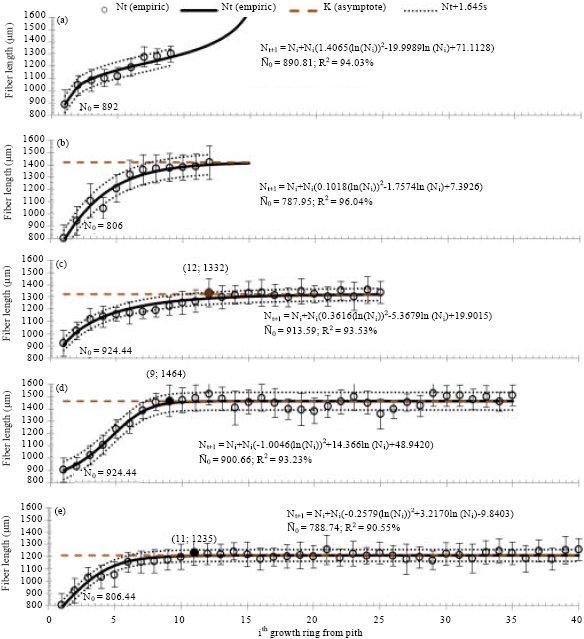
Research Article
Exponential Curve Modification by Linear and Nonlinear Function to Fit the Fiber Length of Teakwood (Tectona grandis)
Faculty of Forestry, Bogor Agricultural University, Campus IPB Darmaga, West Java, Indonesia
Atmawi Darwis
School of Life Sciences and Technology, Bandung Institute of Technology, West Java, Indonesia