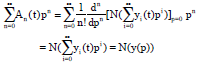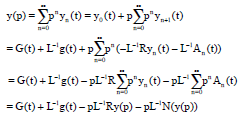Research Article
A Comparison Between Adomian’s Decomposition Method and the Homotopy Perturbation Method for Solving Nonlinear Differential Equations
School of Mathematical Sciences, University Kebangsaan Malaysia, 43600, Bangi Selangor, Malaysia
A.R. Vahidi
Department of Mathematics, Shahr-e-Rey Branch, Islamic Azad University, P.O. Box 18155, Tehran, Iran
Z. Azimzadeh
Department of Mathematics, Science and Research Branch, Islamic Azad University, P.O. Box 14155, Tehran, Iran