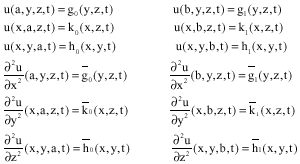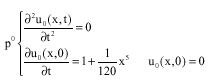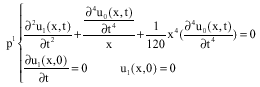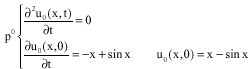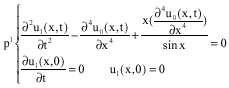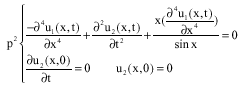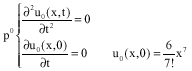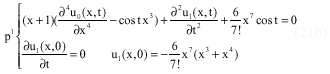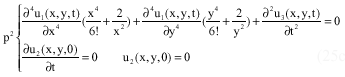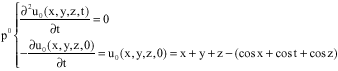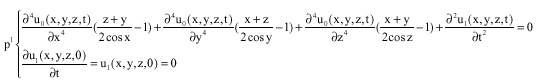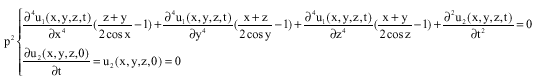Research Article
Explicit Solution of Non-Linear Fourth-Order Parabolic Equations via Homotopy Perturbation Method
Department of Mechanical Engineering, Mazandaran University, P.O. Box 484, Babol, Iran
S.A. Zahedi
Department of Mechanical Engineering, Mazandaran University, P.O. Box 484, Babol, Iran
N. Tolou
Department of Mechanical Engineering, Islamic Azad University, Ayatollah Amoli Branch, Amol, P.O. Box 678, Iran