Research Article
Exergy Based Performance Analysis of a Gas Turbine at Part Load Conditions
Department of Mechanical Engineering Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750, Tronoh, Perak, Malaysia
Syed Ihtsham-Ul-Haq Gilani
Department of Mechanical Engineering Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750, Tronoh, Perak, Malaysia









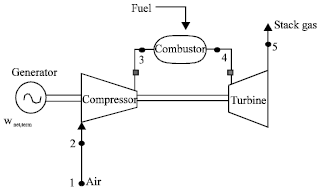
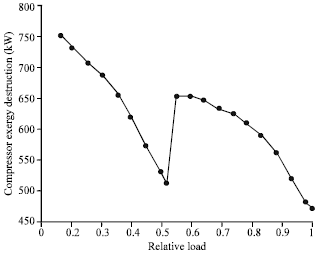

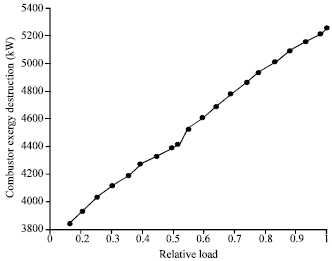
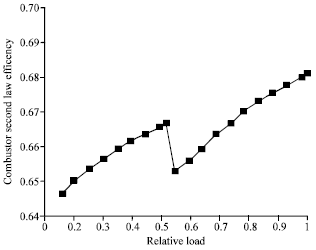
Godspower Reply
I think this paper has simplified my analysis on Exergy