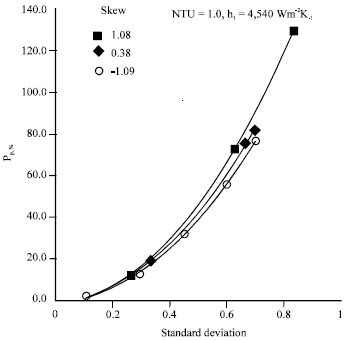
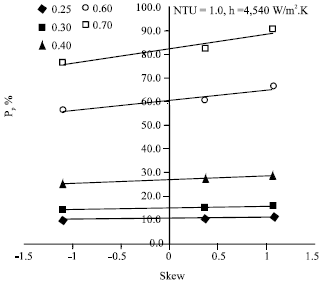
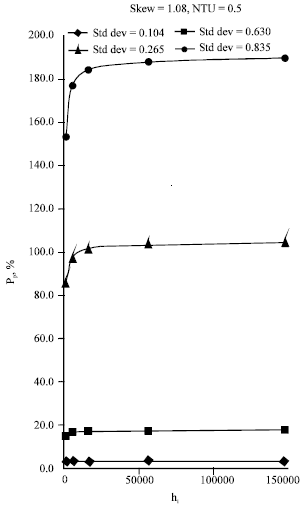
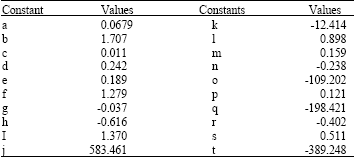
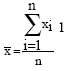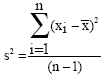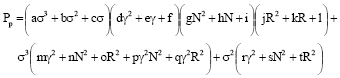Research Article
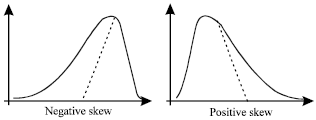
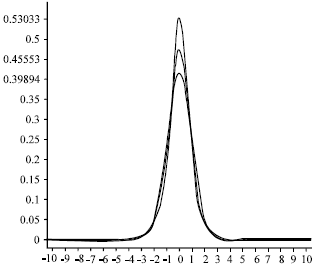
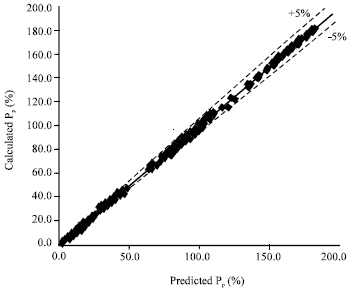
Effect of the Moments of Probability Density Function for Non-uniform Air Flow Distribution on the Hydraulic Performance of a Fin-tube Heat Exchanger
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia
Vijay R. Raghavan
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia