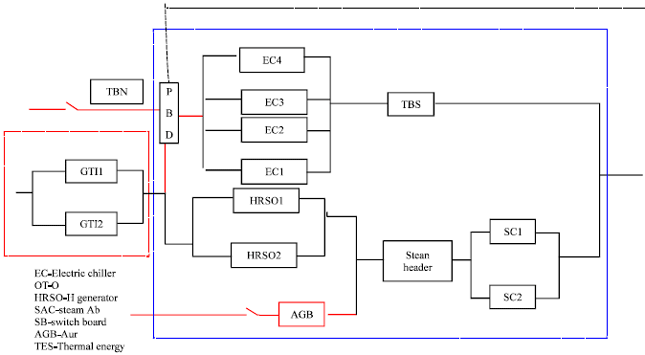
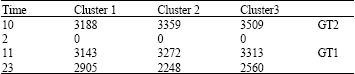
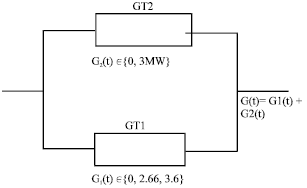
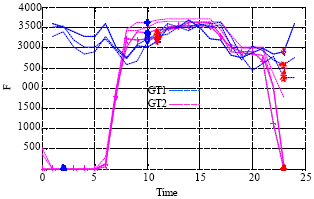
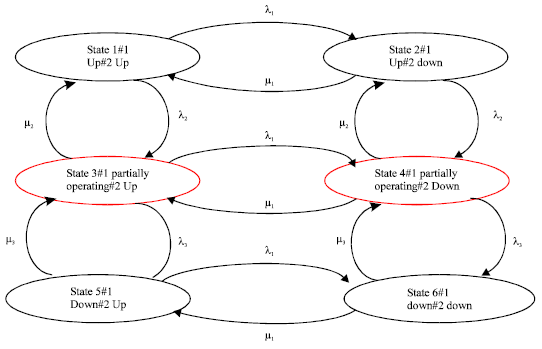
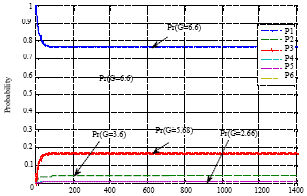
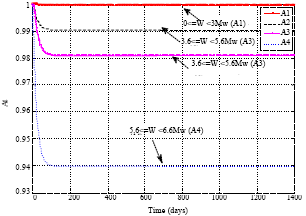
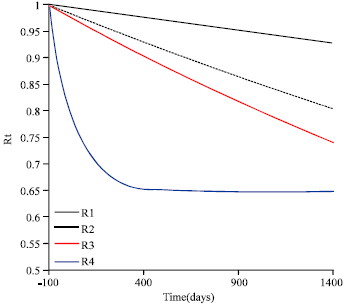
Research Article
A Multi-state Reliability Model for a Gas Fueled Cogenerated Power Plant
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia
Mohd Amin Abd Majid
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia