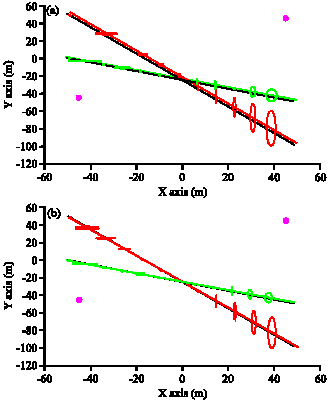
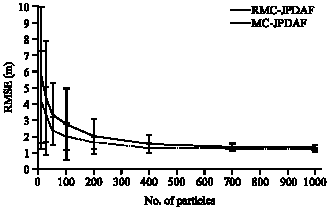
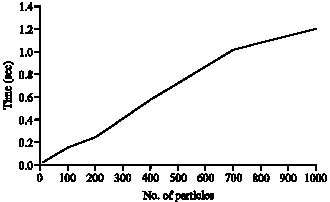
Research Article
Improved Joint Probabilistic Data Association Filter for Multi-Target Tracking in Wireless Sensor Networks
Faculty of Electrical and Computer Engineering, Tabriz University, Tabriz, Iran
M.A. Tinati
Faculty of Electrical and Computer Engineering, Tabriz University, Tabriz, Iran