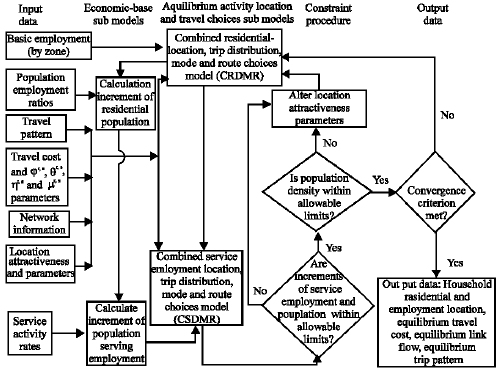
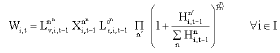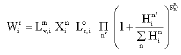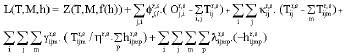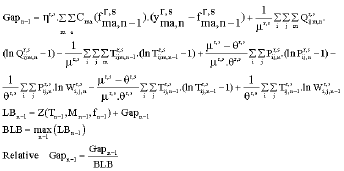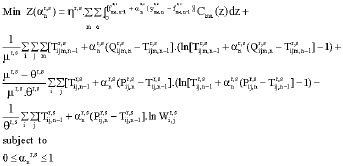Research Article
An Integrated Urban Land Use and Transportation Demand Model Based on Lowry Linage
Department of Civil Engineering, Iran University of Science and Technology,Narmak, P.O. Box 16765-163, Tehran, Iran
Morteza Araghi
Department of Civil Engineering, Iran University of Science and Technology,Narmak, P.O. Box 16765-163, Tehran, Iran