Research Article
Study of Tunneling Transport in Disorder DNA Structures
Faculty of Sciences and Engineering Sciences, Ibn Badiss Mostaganem University
S. Bentata
Faculty of Sciences and Engineering Sciences, Ibn Badiss Mostaganem University
Research on charge transport in DNA is a subject which has risen much interest recently, due to its fundamental roles in biological processes such as the repair mechanism after radiation damage Medvedev and Stuchebrukhov (2001) and in nanotechnologie e.g., construct nanowires directly using the DNA molecules, exploit DNA as a programmable material.
Extensive experimental and theoretical studies on charge transport properties of DNA have appeared in recent years.
These experiments showed that DNA molecules may behaves as an insulator De Pablo et al. (2000), Bockrath et al. (2001), Storm et al. (2001), Gomez-Navarro et al. (2002), a conductor Okahata et al. (1998), Fink et al. (1999) and Kasumov et al. (2001) and even a semi-conducteur Nakayama et al. (2001) and Porath et al. (2000).
This wide range of transport behaviors can be attributed to many experimental complications, one can cite: the type of metallic contact, the nature of devices used to measure conductivity, methods for DNA alignment and drying, the sequence and length of DNA.
Theoretically, several approaches such as one-dimensional quantum mechanical tight-binding models Zhang and Ulloa (2004a, b), Zhu et al. (2004), Klotsa et al. (2005) and Marcia et al. (2005), density-functional theory Taniguchi and Kawai (2004) and nonlinear methods Cuenda and Sanchez (2004) and Peyrard (2004), have been proposed.
In this research, we investigate the tunneling effect in electronic properties of DNA. A DNA molecule can be viewed as 1D chain composed of base pairs A-T and G-C in a typically random order. The gap of base pair A-T is greater than the G-C one, the idea is then to modelle the DNA molecule as a series of barriers and wells. The base pair A-T plays the role of barrier and the G-C one is considered as the well. We have numerically computed various physical quantities such as the transmission coefficient and the probability distribution of the resistance.
Formalism: In quantum mechanic, tunneling effect is particle penetration through the potential barrier even if particle total energy is less than the barrier height V0. This particle, with an energy E and mass m; is described by the Schrödinger equation:
| (1) |
Where
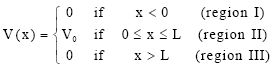 | (2) |
L is the width of a rectangular potential barrier.
Solutions take form:
 | (3) |
Applying the continuity conditions (at x = 0 and x = L) and using matrix representation, we obtain:
| (4) |
Where
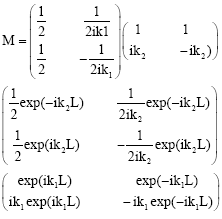 | (5) |
If we denote by:
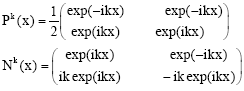 | (6) |
The relation 5 can be written as:
| (7) |
The transmission coefficient, which is the probability for particle to pass through the barrier, is given by:
| (8) |
Within the previous notation:
| (9) |
Here M11 is the M(1, 1) element of matrix M.
Now, generalizing for N regions where the j-th region may be barrier or well and let us call V, B, K the height, thickness and wave vector, respectively. They are defined as come:
| (10) |
| (11) |
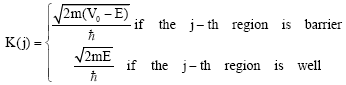 | (12) |
ba is the base pair separation, it’s about 3.4 Å.
We assume that the first region which is at x<0 is a well. Matrix M takes form:
Where
| (13) |
The transmission coefficient is then given by:
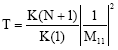 | (14) |
Once the transmission coefficient is determined, the dimensionless resistance is calculated by means the Landauer (1957) formula
| (15) |
To investigate the eigenstate nature in different DNA structure, the probability distribution W of lnρ is reported for various energies. It is well known from Berman et al. (1997) that in the strong localized regime, the function lnρ has a Gaussian distribution of one-dimensional disordered systems:
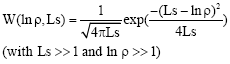 | (16) |
RESULTS AND DISCUSSIONS
This section concerns the statical description of the electronic transport in DNA, by means of numerical calculations of its transmission coefficient with the corresponding resistance probability distribution. We take into account the randomness of the pair sequence, which has important impact on electronic transport.
The value of V0=0.91eV is taken as the gap difference between base pair A-T and G-C Sairam et al. (2005).
Transmission coefficient: Transmission coefficient versus electron incident energy T (E) is plotted. The poly ![]() structure is studied; it’s a periodic and ordered one, each base pair A-T is followed by G-C one. Figure 1a shows in this case the existence of one miniband ranging from 0.4 to 0.97 eV where we remark the tunneling effect for energy values above 0.4 eV. This structure has the same behavior as the ordered semiconductors super lattices one Bentata (2005).
structure is studied; it’s a periodic and ordered one, each base pair A-T is followed by G-C one. Figure 1a shows in this case the existence of one miniband ranging from 0.4 to 0.97 eV where we remark the tunneling effect for energy values above 0.4 eV. This structure has the same behavior as the ordered semiconductors super lattices one Bentata (2005).
Figure 1b that the tunneling probability is 0 for poly (A-T) structure. Transmission takes place only at energy above V0. Above E0 = V0 =0.91 eV, it is observed an oscillatory behavior. The same result is found in quantum mechanic through a single rectangular barrier when the barrier’s width is large Bentata et al. (2000).
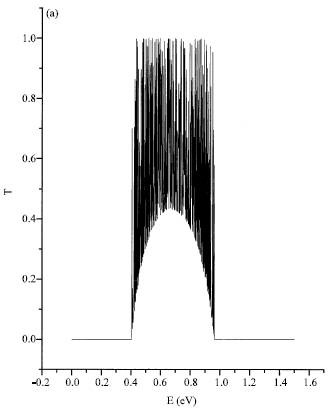 | |
| Fig. 1a: | Transmission coefficient of incident electron energy E for |
 | |
| Fig. 1b: | Transmission coefficient of incident electron energy E for poly(A-T ) DNA |
 | |
| Fig. 1c: | Transmission coefficient of incident electron energy E for different concentration (low concentrations) of base pair (A-T) in DNA molecule |
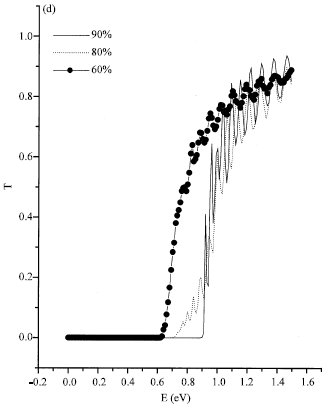 | |
| Fig. 1d: | Transmission coefficient of incident electron energy E for different concentration (high concentrations) of base pair (A-T) in DNA molecule |
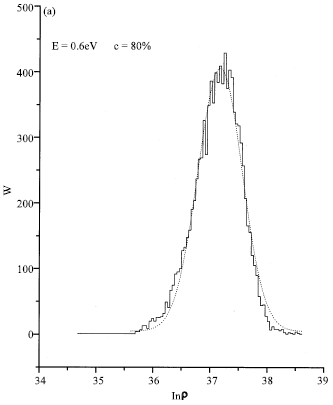 | |
| Fig. 2a: | Fit of Probability distribution for strongly localized states for c = 80% at E = 0.8 eV |
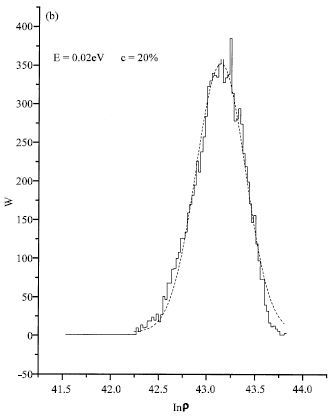 | |
| Fig. 2b: | Fit of Probability distribution W for strongly localized states for c = 20% at E = 0.02 e |
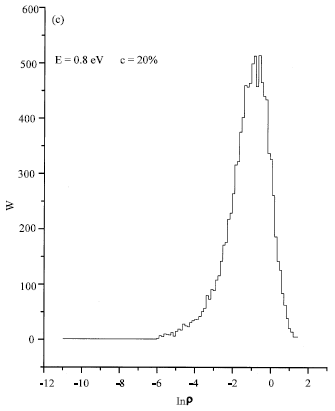 | |
| Fig. 2c: | Probability distribution W of ln ρ for c = 20% at E = 0.8 eV |
We can say that all the base pairs A-T are saw as a single barrier, its thickness is the sum of widths of base pairs A-T. Figure 1c and 1d shows the case where the base pair A-T is randomly distributed along the 1000 base pairs for different concentration. All the results reported in these cases correspond to an average over 600 configurations. We see that there is tunneling effect for 10, 20, 50% of concentration and the transmission coefficient decrease by increasing the concentration of base pair A-T (Fig. 1c); there is no tunneling effect for high concentration (Fig. 1d).
Probability distribution: We have reported the probability distribution of lnρ of various energies. All the results reported here correspond to 104 averages especially to obtain a desired accuracy for the fit of the Probability distribution of the resistance.
The function of lnρ is close to a Gaussian distribution (logarithmically normal in ρ) in the case where E = 0.8eV at concentration c = 80% (Fig. 2a), therefore the existence of strong localized states, Berman et al. (1997). The same result is found in (Fig. 2b) for c = 20% and E = 0.02 eV. When E = 0.8 eV and c = 20% an asymmetric character is observed (Fig. 2c).
We have shown that there is tunneling effect for periodic structure ![]() and also in disorder structure when base pairs A-T appears at low concentration and is randomly distributed along the DNA molecule.
and also in disorder structure when base pairs A-T appears at low concentration and is randomly distributed along the DNA molecule.
We have seen that there is no tunneling effect in poly(A-T) structure and also in disorder one when base pairs A-T appears at high concentration, strong localized states are found in these cases.