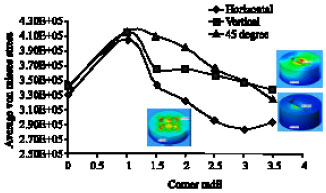
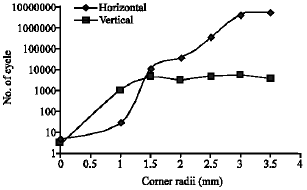
Research Article
The Effect of Corner Radii and Part Orientation on Fatigue Life of Closed-Forging Die
School of Mechanical Engineering, University Sains Malaysia, Engineering Campus,14300 Nibong Tebal, Penang, Malaysia
K.S. Ling
School of Mechanical Engineering, University Sains Malaysia, Engineering Campus,14300 Nibong Tebal, Penang, Malaysia
Z. Samad
School of Mechanical Engineering, University Sains Malaysia, Engineering Campus,14300 Nibong Tebal, Penang, Malaysia
S. Sahudin
School of Mechanical Engineering, University Sains Malaysia, Engineering Campus,14300 Nibong Tebal, Penang, Malaysia