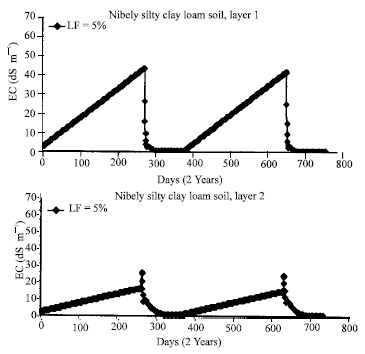
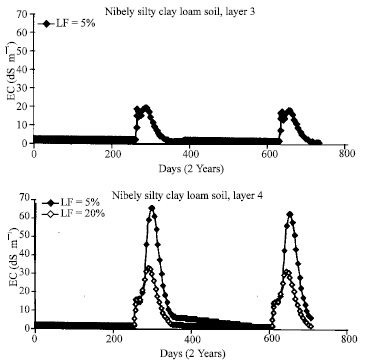
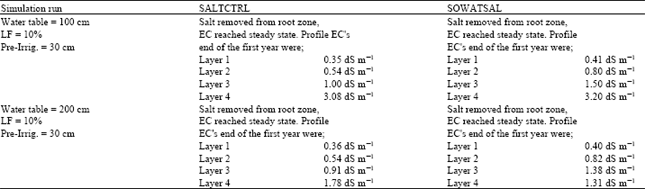
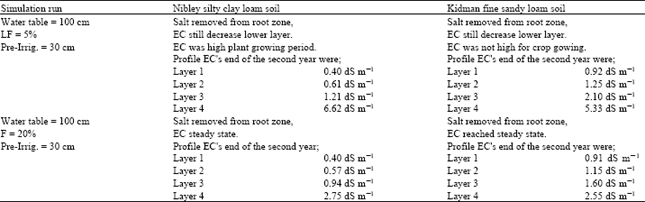
Research Article
Leaching Requirements to Prevent Soil Salinization
Department of Agriculture Structures and Irrigation, Faculty of Agriculture, Ondokuz Mayis University, Kurupelit, Samsun, 55139, Turkey
Lyman S. Willardson
Department of Biological and Irrigation Utah State University Logan, Utah, USA