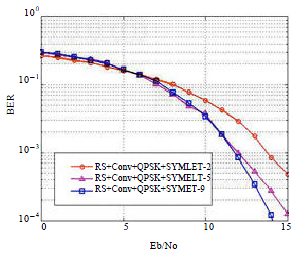
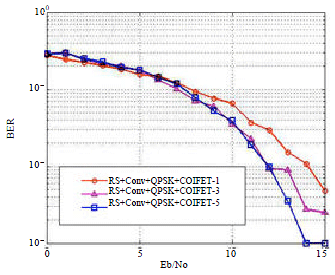
Research Article
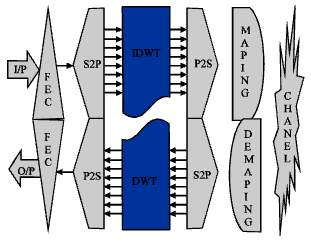
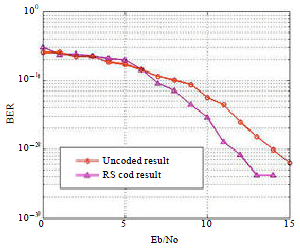
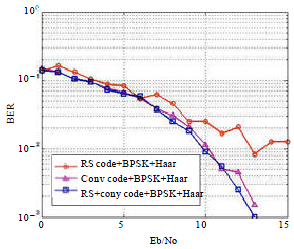
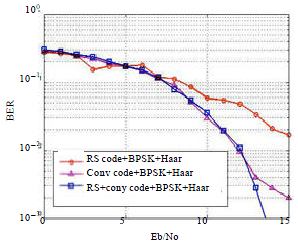
FEC and DWT Guided Multiband Orthogonal Frequency Division Multiplexing (MB-OFDM)-Enriched Quality
Department of ECE, SEEE, SASTRA University, Thanjavur, TamilNadu, India
K. Thenmozhi
Department of ECE, SEEE, SASTRA University, Thanjavur, TamilNadu, India