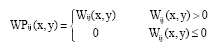Research Article
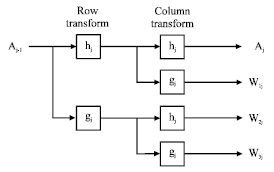
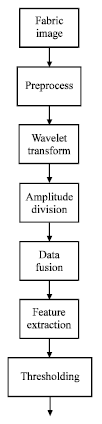
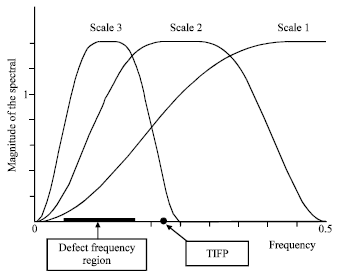
Fabric Defect Detection using Undecimated Wavelet Transform
Key Laboratory of Ministry of Education for Image Processing and Intelligent Control, Department of Control Science and Engineering, Huazhong University of Science and Technology, 1037 Luoyu Road, 430074, Hubei, Wuhan, China
Sun Zhigang
Key Laboratory of Ministry of Education for Image Processing and Intelligent Control, Department of Control Science and Engineering, Huazhong University of Science and Technology, 1037 Luoyu Road, 430074, Hubei, Wuhan, China