Research Article
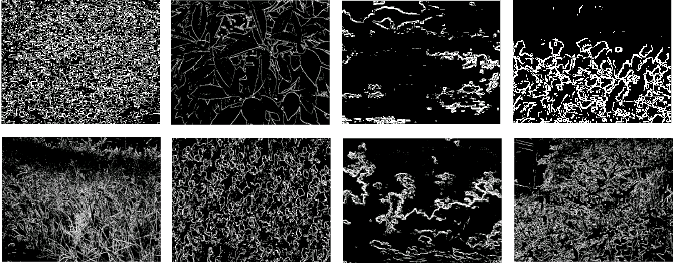
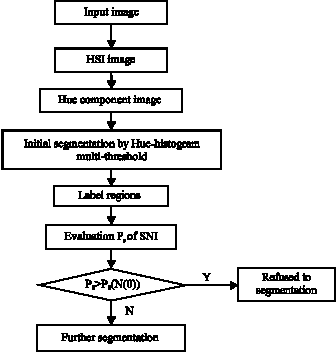
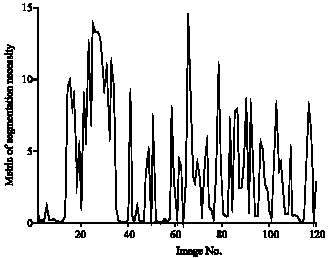
Research on the Image Segmentation Necessity for Regions-Based Image Processing
Department of Information and Communication Engineering, Xi`an Jiaotong University, China
Zhaowei Shang
College of Computer Science, Chongqing University, China
Junyi Shen
Department of Information and Communication Engineering, Xi`an Jiaotong University, China