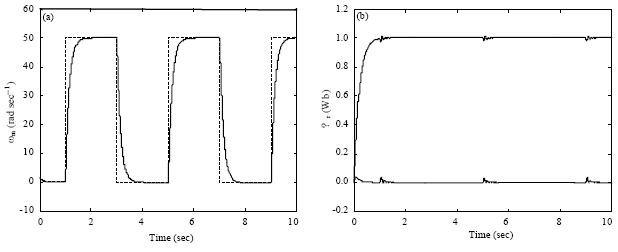
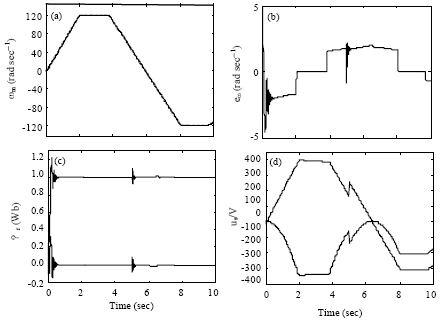
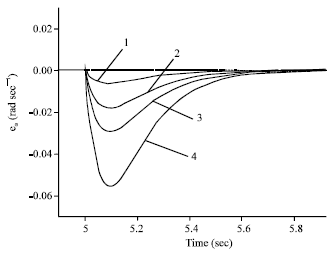
Research Article
Fuzzy Sliding-Mode Control for Induction Motors with Robust H∞ Performance
School of Computer Science, Hunan Institute of Engineering, Xiangtan 411104, Hunan Province, China
Wang Yaonan
School of Electrical and Information Engineering, Hunan University, Changsha 410082, Hunan Province, China
Yang Minsheng
School of Electrical and Information Engineering, Hunan University, Changsha 410082, Hunan Province, China