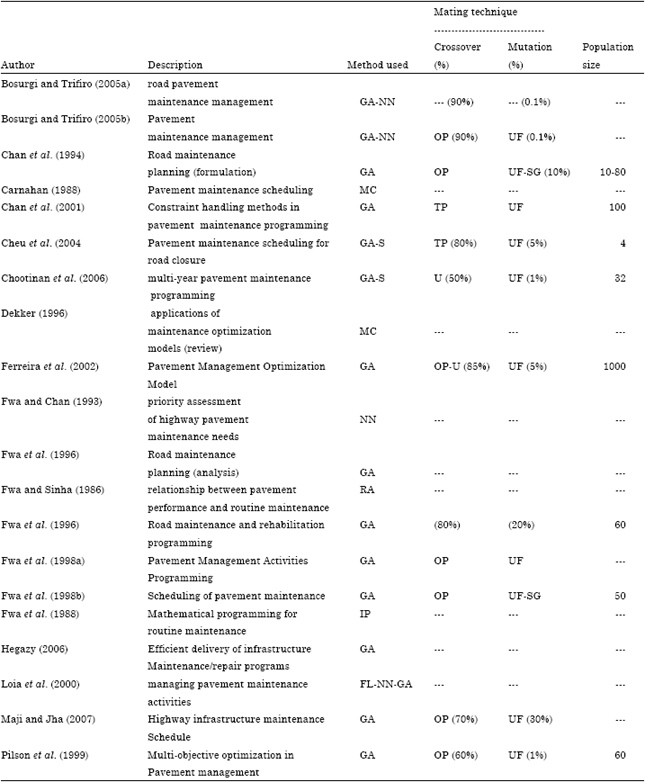
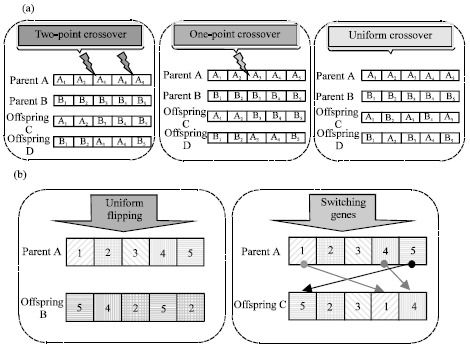
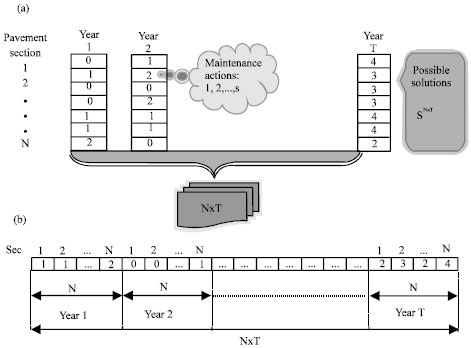
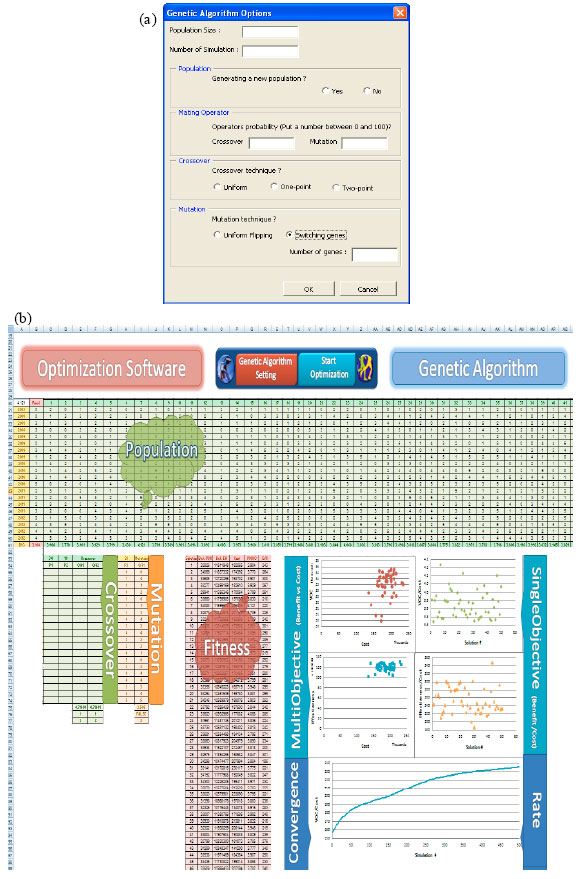
Research Article
Optimum Genetic Algorithm Structure Selection in Pavement Management
Department of Civil and Environmental Engineering, University of Waterloo, Waterloo, ON, N2L 3G1, Canada
Susan L. Tighe
Department of Civil and Environmental Engineering, University of Waterloo, Waterloo, ON, N2L 3G1, Canada