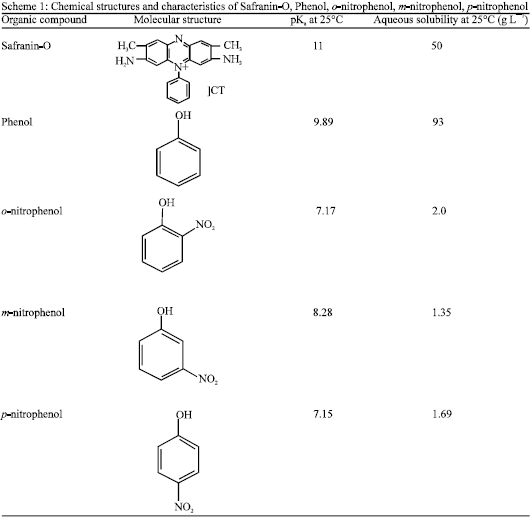
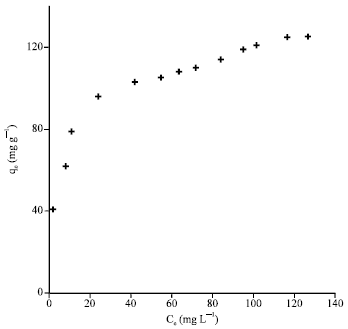
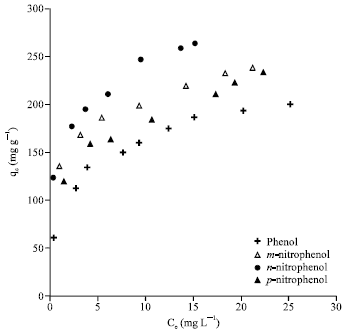
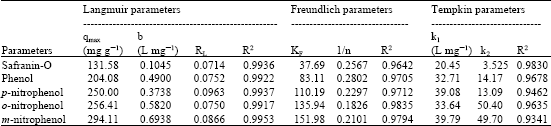
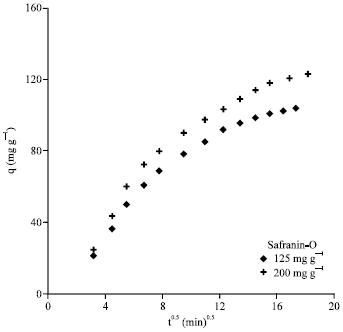
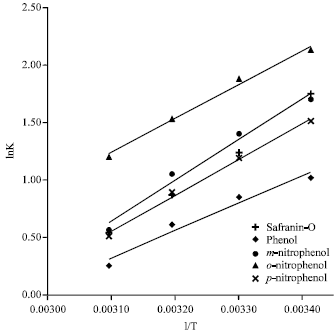
Research Article
Removal of Selected Organic Compounds in Aqueous Solutions by Activated Carbon
Department of Basic Pharmaceutical Sciences, Faculty of Pharmacy, Marmara University, Haydarpalsa 34668, Uskudar, Istanbul, Turkey
S. Kaluc
Department of Basic Pharmaceutical Sciences, Faculty of Pharmacy, Marmara University, Haydarpalsa 34668, Uskudar, Istanbul, Turkey