ABSTRACT
The aim of this study is to analyze a Job Satisfaction (JS) model by using an information theoretic approach based on the semi-parametric Generalized Maximum Entropy (GME) estimator. The GME is used in order to estimate the parameters of the Structural Equation Model (SEM), which represents the theoretical representation of the relationships between the human being and his job. Moreover, thanks to the entropy index measure, the theoretical model is analyzed in its some particular aspects, which can be seen as sub-structures in the relationships.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2011.686.692
URL: https://scialert.net/abstract/?doi=jas.2011.686.692
INTRODUCTION
The focus of this study is on the SEMs, applied to the JS study by using the GME estimator. More specifically, the information theoretic estimator is used to analyze a main model of JS, while in the second step, the normalized entropy measure (Golan et al., 1996) is used to evaluate the contribution of each sub-model, as part of the main model, which is interesting from a JS theoretical point of view and supported by the entropy index measure.
ESTIMATION METHODS FOR THE STRUCTURAL EQUATION MODELS
It’s well known in literature that the estimation methods for analyzing data for SEM in a soft and in a hard way are, respectively, Partial Least Squares (PLS) and Maximum Likelihood Estimation (MLE).
PLS and MLE are in the specification and in the restrictions conceptually different, as numerically different in the parameters estimation values (Wold, 1975), so, the definition of conditions to integrate the two estimation methods in a unique strategy of analysis, is not an easy practicable way. As a consequence of these distinct features, the two approaches has been reasonably considered as alternative instruments to be used according with the data availability, the conceptual assumptions, the theory background, the objective of the research and so on.
A middle way between the soft and hard modelling is represented by the GME estimation method. This method allows to explore the data by using a soft approach that can give a general view of the relationships among the variables and some indications about aspects that can be deeply investigated. This exploration should be made without taking into account restrictions about sample size, number of variables or distributional assumptions on the errors terms.
In the next paragraphs the GME estimation method and the use of normalized entropy index are presented to evaluate the sub-structure in the data.
The generalize maximum entropy estimation method: The GME method (Golan et al., 1996) represents a semi-parametric estimation method for the SEM (Al-Nasser, 2003; Ciavolino and Al-Nasser, 2009; Ciavolino, 2009) which works well in case of ill-behaved or nonlinear data. The SEM (Jöreskog, 1973), can be formulated in a system of equations as follows:
| (1) |
| (2) |
| (3) |
These equations consist of two main parts: the first part is the Structural Model (1) and represents the linear relationships among the latent variables; where η is the vector of the m endogenous latent variables, ξ the vector of the n exogenous latent variables, x and y, respectively the vectors of the q and p manifest exogenous and endogenous variables.
The coefficient matrices B and Γ contain the path coefficients of the effects of the endogenous on the endogenous variables and the exogenous on the endogenous variables.
The second part is the Measurement Model, representing the relationships between the manifest and the latent variables: endogenous in Eq. 2 and exogenous in Eq. 3.
The coefficient matrices Λy and Λx measure the relationships between the manifest and latent variables, endogenous and exogenous.
The vectors τ, ε and δ, are the structural and the measurement errors vectors. For the definition of the whole model, four other matrices have to be defined. The co-variance matrices: Φ, between the latent variables ξ; Ψ, between the error term τ; Θe, between the error term ε; Θδ, between the error term δ. The three SEM equations can be re-formulated as a unique function model:
| (4) |
With m endogenous latent variables, n exogenous latent variables and p and q manifest endogenous and exogenous variables. The GME approach considers the re-parameterization of the unknown parameters and the disturbance terms as a convex combination of expected value of a discrete random variable. The coefficient matrices, B, Γ, Λy, Λx and the co-variance matrices, Φ, Ψ, Θe, Θd, are all re-parameterized as expected values of discrete random variable with M fixed points1 for the coefficients and N for the errors ![]()
![]()
![]()
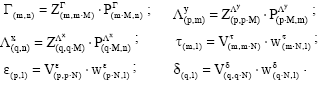 |
The matrices Z and V are diagonal and the generic matrix element is represented respectively by the vectors Z'k = [–c –c/2 0 c/2 c] with {k = 1, . . ., m; p; q} and V'h = [–b –b/2 0 b/2 b]with {h = 1, . . ., n; p; q}. These vectors define the support space and are called fixed points. Usually they are composed by five elements (M=N=5), but the fixed points vh, related to the sample observed, can be chosen by Chebychev’s inequality (Pukelsheim, 1994).
Given the re-parameterization and the re-formulation, the GME system can be expressed as a constrained non-linear programming problem. The coefficients and the error terms are estimated by recovering the probability distribution of the discrete random variables set. The vectors pB=vec(PB), pΓ=vec(PΓ), pΛy=vec(PΛy), pΛx=vec(PΛx), are obtained by using the vec operator of the matrices PB, PΓ, PΛy, PΛx. The probability vectors: pB, pΓ, pΛy, pΛx, wτ, wε, wδ, are calculated by maximizing the following Shannon (1948) entropy function:
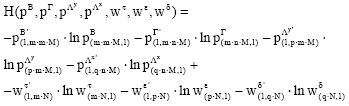 | (5) |
subjected to the consistency constraint, which represents the information about the model reported in the Eq. 4 and normalization constraints, that means, the sum of both coefficients and the error terms probability vectors have to be equal to 1:
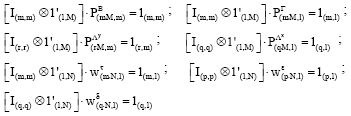 |
The GME provides, also, the normalized entropy measure (Golan et al., 1996; Golan, 2008) that quantifies the level of information in the data, giving a global measure of the goodness of relationships, hypothesized in a model.
The normalized entropy measure: The normalized entropy measure can be expressed by the following formulation:
| (6) |
The normalized index is a measure of the uncertainty information, where –p' · lnp is the Shannon’s entropy function, defined only for the coefficients probabilities; K is the number of the coefficients to be estimated and M is the number of the fixed points.
The quantity K · lnM represents maximum uncertainty, since in the case of no contribution of one variable, the entropy coefficient is that of a uniform distribution of the K variables with M outcomes:
| (7) |
If , there is no uncertainty, while means total uncertainty. The normalized entropy measure is used to derive the log-likelihood ratio statistic:
| (8) |
Which, under the null hypothesis that all the parameters are zero, converges in distribution to a χ2 with K degrees of freedom, where the degrees of freedom are the number of constraints imposed. Moreover a Pseudo-R2 can be defined as:
| (9) |
The R2 is a measure to derive a goodness of fit of the model, where the value 0 implies no informational value of the data and 1 implies perfect certainty or perfect in-sample prediction. This measure is the same as the information index in Soofi (1992).
The normalized entropy measure can be used also as a method for the selection of the explicative variables. In fact, it is possible to calculate the Shannon’s entropy function for one predictor (with K=1) as: –pk' · lnpk; so, the uncertainty information of the kth explicative variable is the following:
| (10) |
The normalized entropy measure can determine the uncertainty information of a specified sub-structure in the data. Let consider a SEM where according with some theoretical assumptions, can be divided into S elements, whose generic sth element defines a sub-model with a specific number of coefficients cs, such that cs�K. The level of the uncertainty information of the specified sth sub-model can be defined as follow:
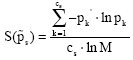 | (11) |
The quantity above defined expresses the contribution of the sth part of the model in making the uncertainty information of the whole SEM system. The normalized entropy measure of whole SEM, in case the sub-models are mutually exclusives, can be expressed as the weighted average of the normalized entropy measure of each sub-model, as follow:
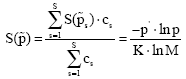 | (12) |
This measure can be a suitable tool to understand the percentage of information explained by the different sub-models that can be specified as a part of the principal model.
THE JOB SATISFACTION EVIDENCE
In order to show an application of the GME as method to detect SEM sub-structures in the data and to understand the human labor aspects, a job satisfaction model is presented. Data were gathered from a sample composed of 87 employees working in the private sector in the province of Lecce, a small town situated in the South of Italy.
The tool for studying the JS was a questionnaire, face to face administered and subdivided into specific evaluation areas for investigating on JS related to workers’ attitudes.
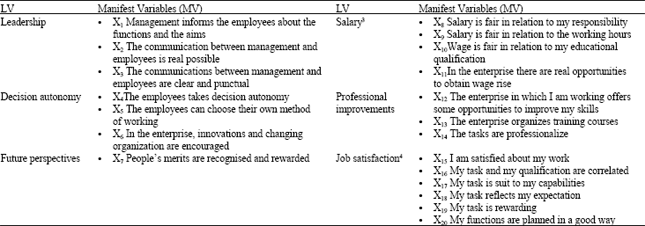
The questionnaires was made up of 20 items, used for measuring 6 latent constructs (Leadership, Future Perspective, Decision Autonomy, Salary, Professional Improvement and Job Satisfaction2) which represent both intrinsic and extrinsic aspects of one’s job (Carpita, 2009). Each item is an indicator (manifest variable) having the form of a positive statement concerning several elements of the working reality of the subjects interviewed.
The workers were asked to evaluate the statements by using an ordinal scale consisting in five response choices ranging from 1 (total disagree) to 5 (maximum agree). Table 1 shows the Manifest Variables (MVs) related to each Latent Variables (LVs) for the job satisfaction measurement model Ciavolino (2009).
The main model is reported in Fig. 1, where the SEM graphical representation considers: latent variables, defined by using the Greek letters and drawn by circles; manifest variables, defined by Latin letters and drawn by rectangles.
The main model of job satisfaction: The Fig. 2 shows the GME estimated structural coefficients (β and γ) of the theoretical JS model above defined. All the causal relationships are significant. The GME provides first step of explorative analysis in order to evaluate the relationships among the selected latent and manifest variables, without requiring any assumptions, with respect to the errors distribution, the sample size and the multi-collinearity.
| Table 1: | Latent and manifest variables |
 | |
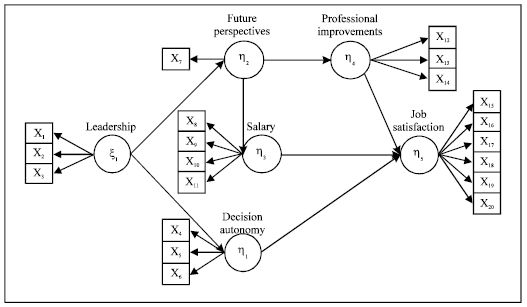 | |
| Fig. 1: | The path diagram of the job satisfaction main model |
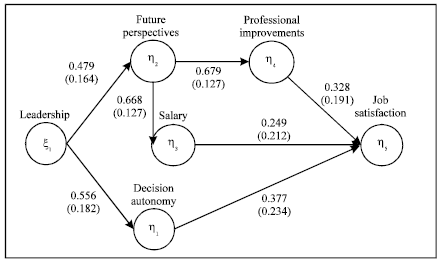 | |
| Fig. 2: | The estimate coefficients of the job satisfaction main model |
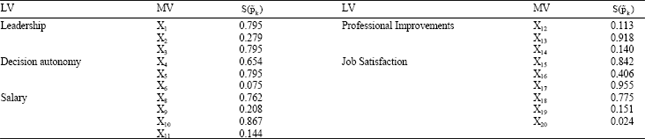
| Table 2: | The normalized entropy measures of manifest variables |
 | |
The first Job Satisfaction model hypothesized involves a remark about the Leadership style (Ciavolino and Dahlgaard, 2009; Dahlgaard and Ciavolino, 2007). The main challenges for leaders are to build a long-term vision, to increase commitment, to build teams and coalitions in order to reach required organizational objectives (Kuean et al., 2010). This consideration lie at the bottom of the decision to link the latent variable Leadership with the Decision Autonomy (0.479) and the future perspectives (0.556) constructs.
The future perspectives in their turn influence the perception about Salary (0.668) and Professional Improvements (0.679). It is reasonable to hypothesize that, if an enterprise offers to the employees the chance to obtain promotions and embraces a meritocratic principle by recognizing and rewarding workers’ merits (considering a long term perspective), employees are incited to improve their skills and to better their performance. Salary (0.249) and Professional Improvements (0.328) act on Job Satisfaction. The Salary represents one of the most important extrinsic feature, taking into account monetary aspect, but the LV above defined is more related to the distributive fairness and consequently the non-monetary (e.g., working hours or professional development) aspects of the work. Moreover opportunity to achieve professional improvements seems to have an higher impact than the salary. In the model theorized Decision Autonomy, influenced by Leadership, acts on Job Satisfaction (0.377). An enterprise democratically regulated, in which workers can propose suggestions and choose their own working method taking part in the decision-making process.
The sub-models analysis: Table 2 reports the values of the normalized entropy for each manifest variable that measures the reduction in uncertainty information of each manifest variable. The quantity ![]() gives information about the distance between the probability distribution of each coefficient and a uniform distribution. The value
gives information about the distance between the probability distribution of each coefficient and a uniform distribution. The value ![]() implies a strong relationship, while the value
implies a strong relationship, while the value ![]() implies the variable is extraneous from the model.
implies the variable is extraneous from the model.
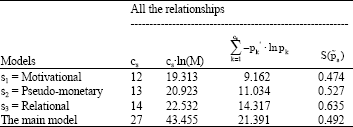
| Table 3: | The normalized entropy measures of each sub-model |
 | |
This table could be also interpreted as a further item-scale analysis which takes into account the casual relationships among the LVs. In this case it is possible to read that same items, as for instance the X13 for the Professional Improvements or X18 for the Job Satisfaction, could be considered not belonging the this JS model. These results suggest us that additional considerations can be done on the specification of the measurement model, but for the aim of this paper we will take all the manifest variables.
The first explorative study allows to test the validity of the theoretical hypotheses based on the main model, by analyzing the statistical features of the structural and measurement relationships, but, at the same time, it allows to evaluate the contribution of each sub-model. Leaving out the interpretation of the manifest variables, we focalize on how the normalized entropy measure can reflect the uncertainty information of each above specified structure in the model (supra §2.2).
By reminding this, three sub-models have been individuated with the following structure: The sub-models contain the LV Future Perspective as exogenous variable which, in the first sub-model, acts on the Professional Improvements; in the second sub-model acts on the Salary. These endogenous variables, in both of cases, have a direct and causal action on the JS. The former sub-model has been named Motivational Model (s1) the latter is the Pseudo-Monetary5 (s2) one. The third sub-model is the so called Relational model (s3) linking the exogenous variable Leadership to the Decision Autonomy, related to Job Satisfaction.
Table 3 contains the results of the normalized entropy measures related to each sub-model.
The number of fixed points M is equal to 5. The first two columns “cs and cs·ln(M)” report, respectively: the number of constraints on the variables, that means the number of coefficients estimated and the entropy value in case of maximum uncertainty condition.
The following two columns “![]() and
and ![]() ”, represent respectively: the entropy estimated and normalized entropy measure to evaluate the informational content of the estimates with 1 reflecting uniformity (complete ignorance) of the estimates and 0 reflecting perfect knowledge (supra §2.2).
”, represent respectively: the entropy estimated and normalized entropy measure to evaluate the informational content of the estimates with 1 reflecting uniformity (complete ignorance) of the estimates and 0 reflecting perfect knowledge (supra §2.2).
The first three rows report the results of the three sub-models (s1=Motivational, s2=Pseudo-Monetary, s3=Relational), while in the last row there is the result of the Main Model.
In this case the sub-models are not disjoint, that means, some parts of one specific model are also a part of another model (the common parts are the future perspective and the job satisfaction), so the whole SEM system normalized entropy measure cannot be obtained as a entropy weighted average of each sub-models (Eq. 12).
The JS main model has a goodness of fit equal to 0.508, which represents a good level of reduction of uncertainty generated by this theoretical model. The contributions of each sub-model in reduction of uncertainty are respectively ![]() =0.474,
=0.474, ![]() =0.572,
=0.572, ![]() = 0.635.
= 0.635.
Although the model are not disjoint, it is interesting to see that same sub-models have a value of ![]() smaller then the main model, meaning that the introduction of the other variables and coefficients, improve the interpretability of the JS model and the reduction of the uncertainty.
smaller then the main model, meaning that the introduction of the other variables and coefficients, improve the interpretability of the JS model and the reduction of the uncertainty.
In particular the Relational Model, with an ![]() seems to give no so strong contribution in the reduction of the uncertainty information of the main model.
seems to give no so strong contribution in the reduction of the uncertainty information of the main model.
On the other hand, Motivational Model and Pseudo-Monetary are the most important parts in the contribution in making the information of the whole SEM system. As the matter of the fact, the contribution of each sub-model is quite similar and very close the entropy expressed by the main. The interpretation is that these two part of the main model represent two of the main important aspects to be considered in the explanation of the JS, because the introduction of other parameters don’t give a so high impact in the reduction of uncertainty.
CONCLUSIONS AND DISCUSSION
This study has focused on a study of the JS based on a survey composed by 87 Italian employees working in the private sector, in order to show the GME as method to detect SEM sub-structures in the data and to understand the human labor aspects.
It has been shown how normalized entropy measure can be a suitable tool to improve the interpretative overall results by dividing and measuring the contribution of each part of the model in making the reduction of the uncertainty information.
This method gave us the chance to strengthen the theoretical substratum of the model and to pick out some sub-models for better understanding the working dynamics for JS (Hosseinian et al., 2008).
Through the Motivational Model it is emerged that the Future Perspective emphasizes the importance of the Professional Improvements during the working life to improve the JS. Instead, through the Pseudo-Monetary Model it is emerged the Future Perspective influence on the perception about own Salary. In this theoretical position, Salary is a no monetary variable because it doesn’t contain monetary measures but social measures. Besides, given the Future Perspective causal action on the Salary, this last has been defined such as dynamic subjective variable which changes in according to future expectations.
The last local structure analysis of Job Satisfaction has been developed on the model specifying causal relationships between Leadership, Decision Autonomy and Job Satisfaction. It is emerged that the so called Relational Model in the reduction of uncertainty information of the main model is not so strong. It is undoubted that the quality of interpersonal exchange between superiors and a subordinate can make up an important element of the employee's job satisfaction and for the performance of the enterprise, for this reason this sub-model of the main JS model should be better studied or measured in the survey used for the analysis, to improve the contribution in the specification of the JS.
In conclusion, the results obtained by conducting the SEM GME analysis allowed fixing some relevant points to be taken into account in implementing policies aiming at realizing an efficient and satisfying organization of work. In this sense individual components of work (and their satisfaction) are to be considered a focal resource for enterprises which decide to invest on human capital giving rise to a series of activities which enable working people and their employing organizations to agree about the objectives and nature of their working relationships and secondly, ensures that the agreement and goals are fulfilled.
REFERENCES
- Kuean, W.L., S. Kaur and E.S.K. Wong, 2010. The relationship between organizational commitment and intention to quit: The Malaysian companies perspectives. J. Applied Sci., 10: 2251-2260.
CrossRef - Hosseinian, S., Y. Seyedeh-Monavar, Z. Shaghayegh and A. Fathi-Ashtiani, 2008. Emotional intelligence and job satisfaction. J. Applied Sci., 8: 903-906.
CrossRefDirect Link - Al-Nasser, A.D., 2003. Customer satisfaction measurement models: Generalized maximum entropy approach. Pak. J. Stat., 19: 213-226.
Direct Link - Ciavolino, E. and A.D. Al-Nasser, 2009. Comparing generalized maximum entropy and partial least squares methods for structural equation models. J. Nonparam. Stat., 21: 1017-1036.
CrossRefDirect Link - Ciavolino, E. and J.J. Dahlgaard, 2009. Simultaneous equation model based on generalized maximum entropy for studying the effect of the management's factors on the enterprise performances. J. Applied Statist., 36: 801-815.
CrossRef - Dahlgaard, J.J. and E. Ciavolino, 2007. Analysing management factors on enterprise performance. Asian J. Q., 8: 1-10.
Direct Link - Golan, A., 2008. Information and entropy econometrics-a review and synthesis. Foundation Trends Econ., 2: 1-145.
Direct Link - Shannon, C.E., 1948. A mathematical theory of communication. Bell Syst. Tech. J., 27: 379-423.
Direct Link - Soofi, E.S., 1992. A generalizable formulation of conditional logit with diagnostics. J. Am. Statistical Assoc., 87: 812-816.
Direct Link








