ABSTRACT
In this study, we implement a relatively new analytical technique, the Adomian Decomposition Method (ADM), for solving Abelian differential equations. The analytical and numerical results of the equations have been obtained in terms of convergent series with easily computable components. The method is applied to solve two problems. The current results are compared with these derived from the established Runge-Kutta method in order to verify the accuracy of the ADM. It is shown that there is excellent agreement between the two sets of results. This finding confirms that the ADM is powerful and efficient tool for solving Abelian differential equations.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2008.1962.1966
URL: https://scialert.net/abstract/?doi=jas.2008.1962.1966
INTRODUCTION
In this study, we consider the Abelian differential equations of the type:
| (1) |
with initial condition
| (2) |
where, fj (x), j = 0,..., 3, are given continuous, linear or non-linear functions and c is a real finite constants.
The Adomian Decomposition Method (ADM) (Adomian, 1988, 1991) will be effectively used to approach Eq. 1. The Adomian algorithm introduces the solution in the form of a rapidly convergent series with elegantly computable terms. In the literature, the decomposition method has been used to obtain approximate solutions of a large class of linear or nonlinear differential equations (Adomian, 1988, 1991, 1994; Adomian et al., 1991; Adomian, 1994). This computational method yields analytical solutions and has certain advantages over standard numerical methods. It is free from rounding off errors as it does not involve discretization and does not require large computer obtained memory or power.
ADM consists of splitting the given equation into linear and nonlinear parts, inverting the highest-order derivative operator contained in the linear operator on both sides, identifying the initial and\or boundary conditions and the terms involving the independent variable alone as initial approximation, decomposing the unknown function into a series whose components are to be determined, decomposing the nonlinear function in terms of special polynomials called Adomian`s polynomials and finding the successive terms of the series solution by recurrent relation using Adomian`s polynomials. ADM is quantitative rather than qualitative, analytic, requiring neither linearization nor perturbation and continuous with no resort to discretization and consequent computer-intensive calculations. The method is well addressed in (Guellal and Cherruault, 1995).
The convergence of the decomposition series has been investigated by several researchers, Abbaoui and Cherruault (1996), Adomian (1988), Seng et al. (1996), Cherruault (1989) and Cherruault and Adomain (1993). They obtained some results about the speed of convergence of this method. Abbaoui and Cherruault (1996) have proposed a new approach of convergence of the decomposition series. The authors have given a new condition for obtaining convergence of the decomposition series to the classical presentation of the ADM in Abbaoui and Cherruault (1996). In this study we use ADM for obtaining approximate solutions of the Abelian differential equation. In the case of f3 (c) = 0, Eq. 1 reduces to the well known Riccati equation. The importance of this equation usually arises in the optimal control problems. The feed back gain of the linear quadratic optimal control depends on a solution of a Riccati differential equation which has to be found for the whole time horizon of the control process (Zill, 1997; Bulut and Evans, 2002) applied the decomposition method for solving Riccati differential equation. El-Tawil et al. (2004) applied the multistage Adomian,s decomposition method for solving Riccati differential equation and compared the results with standard ADM. Recently, Momani and co-workers extended the method to fractional differential equations, (Momani, 2006; Momani and Shawagfeh, 2006; Momani and Qaralleh, 2007). In this study, the Adomian Decomposition Method (ADM) proposed in (Adomian, 1988, 1991) is used to handle the non-linear differential Equations (1). Comparisons are also made between the present method and fourth-order Runge-Kutta method to show the efficiency of the present method.
ANALYSIS OF METHOD
Here, we review the Adomian decomposition method by following the procedures of (Adomian, 1988, 1991). However the same techniques can be applied on other system of equations (Bulut and Evans, 2002). To introduce this method, we consider the operator equation Fu = G, where F represents a general nonlinear ordinary differential operator and G is a given function. The linear part of F can be decomposed into L + R, where L is easily invertible and R is the remainder of F. Thus the equation may be written as:
| (3) |
where, N is a nonlinear operator, L is the highest-order derivative which is assumed to be invertible, R is a linear differential operator of the order less than L and G is the source term.
The method is based on applying the operator L-1 formally to the expression
| (4) |
So by using the given conditions we obtain
| (5) |
where, h is the solution of the homogeneous equation Lu = 0, with the initial/boundary conditions.
The problem now is the decomposition of the nonlinear term Nu. To do this, Adomian developed a very elegant technique as follows:
Define the decomposition parameter λ as ![]() , then N (u) will be a function of λ, u0, u1,..., next expanding N (u) in Maclurian series with respect to λ we obtain
, then N (u) will be a function of λ, u0, u1,..., next expanding N (u) in Maclurian series with respect to λ we obtain ![]() , where
, where
| (6) |
where, the components of An are the so-called Adomian polynomials, they are generated for each non-linearity, for example, for N (u) = f(u), the Adomian polynomials are given as:
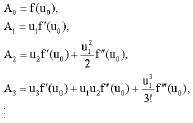 |
They can be found from the formula (Adomian, 1990):
| (7) |
where, f(k) (u0) = dkf(u0)/ duk and C (k, n) means the sum of possible products of k components of u, whose subscripts add to n, divided by the factorial of the number of repetitions.
Now, we parameterize Eq. 3 in the form
| (8) |
where, λ is just an identifier for collecting terms in a suitable way such that un depends on u0, u1,..., un-1 and we will later set λ = 1
| (9) |
Equating the coefficients of equal powers of λ, we obtain
 | (10) |
And in general
| (11) |
Finally an N-term approximate solution is given by
and the exact solution is ![]() .
.
APPLICATION AND NUMERICAL RESULTS
The decomposition method requires that the Abelian differential Eq. 1 be expressed in terms of operator form as
| (12) |
where, ![]() .
.
The ADM suggests the solution y(x) be decomposed by the infinite series of components
| (13) |
and the nonlinear terms
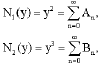 | (14) |
where, An and Bn are the Adomain polynomials of y2, y3, respectively. The first four components of Adomain polynomials reads
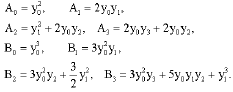 | (15) |
Substitution the decomposition series Eq. 13 and 14 into both sides of (12), then applying the inverse L-1 gives:
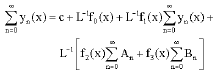 | (16) |
From this equation, the iterates are determined by the following recursive way:
| (17) |
The decomposition method provides a reliable technique that requires less work if compared with traditional techniques. To give a clear overview of the methodology, the following two examples will be discussed. All the results are calculated by using the symbolic calculus software Mathematica.
Example 1: Consider the following Abelian differential equation
| (18) |
subject to the initial condition
| (19) |
Substituting Eq. 18 and the initial condition Eq. 19 into Eq. 17 and using Eq. 16 to calculate the Adomian polynomials, yields the following recursive relation
| (20) |
Using the above recursive relationship and Mathematica, the first few terms of the decomposition series are given by:
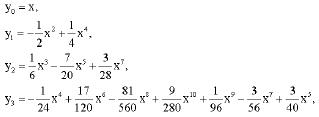 |
other components are determined similarly. The fourth-term approximate solution is given by
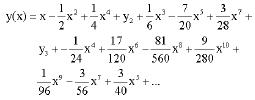 | (21) |
The graphs of the approximate solution Eq. 21 and the solution obtained by fourth-order Runge-Kutta method are given in Fig. 1. It can be seen that the results from the ADM match the results of the Runge-Kutta method very well, which implies that the ADM can predict the motion of the Abelian differential equation accurately for the region under consideration.
Example 2: Consider the following Abelian differential equation
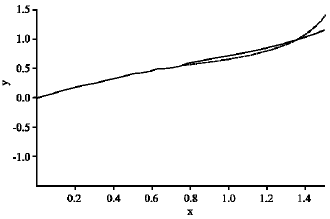 | |
| Fig. 1: | Plots of y versus x. Runge-Kutta method (—); Eq. 21 (- - -) |
| (22) |
subject to the initial condition
| (23) |
Substituting Eq. 22 and the initial condition Eq. 23 into Eq. 17 and using Eq. 16 to calculate the Adomian polynomials, yields the following recursive relation
| (24) |
Using the above recursive relationship and Mathematica, the first few terms of the decomposition series are given by
 |
other components are determined similarly. The fifth-term approximate solution is given by
 | |
| Fig. 2: | Plots of y versus time x. Runge-Kutta method (—); Eq. (25) (- - -). |
 | (25) |
Numerical results are shown in Fig. 2. It is clear, as in the previous case, that the ADM solution works very well. Errors are small and may be made smaller by using more terms of the ADM truncated series.
CONCLUSIONS
In this study, the Adomian decomposition method has been successfully applied to finding the approximate solution of the Abelian differential Eq. 1. All of the examples show that the results of the present method are in excellent agreement with those obtained by the fourth order Runge-Kutta method. The Adomian decomposition method was clearly very efficient and powerful technique in finding the solutions of the proposed equation. The reliability of the method and reduction in the size of computational domain give this method a wider applicability.
REFERENCES
- Abbaoui, K. and Y. Cherruault, 1996. New ideas for proving convergence of decomposition method. Comput. Math. Applied, 29: 103-108.
CrossRef - Adomian, G., 1988. A review of decomposition method in applied mathematics. J. Math. Anal. Appl., 135: 501-544.
CrossRef - Adomian, G., 1990. A review of the decomposition method and some recent results for nonlinear equations. Comput. Math. Applic., 21: 101-127.
CrossRefDirect Link - Adomian, G., 1990. A review of the decomposition method and some recent results for nonlinear equations. Comput. Math. Applic., 21: 101-127.
CrossRefDirect Link - Adomian, G., R.C. Rach and R.E. Meyers, 1991. An efficient methodology for the physical sciences. Kybernetes, 20: 24-34.
CrossRef - Bulut, H. and D.J. Evans, 2002. On the solution of the Riccati equation by the decomposition method. Int. J. Comput. Math., 79: 103-109.
CrossRef - Cherruault, Y. and G. Adomian, 1993. Decomposition methods: A new proof of convergence. Math. Comput. Modelling, 18: 103-106.
CrossRefDirect Link - El-Tawil, M.A., A.A. Bahnasawi and A. Abdel-Naby, 2004. Solving Riccati differential equation using Adomian's decomposition method. Applied Math. Comput., 157: 503-514.
CrossRef - Guellal, S. and Y. Cherruault, 1995. Application of the decomposition method to identify the distributed parameters of an elliptical equation. Math. Comput. Model., 21: 51-55.
CrossRef - Momani, S., 2006. Non-perturbative analytical solutions of the space and time-fractional Burgers. Chaos Solitons Fractals, 28: 930-937.
CrossRef - Momani, S. and N. Shawagfeh, 2006. Decomposition method for solving the fractional Riccati differential equation. Applied Math. Comput., 182: 1083-1092.
CrossRef - Momani, S. and R. Qaralleh, 2007. Numerical approximations and Pade approximants for a fractional population growth model. Applied Math. Model., 31: 1907-1914.
CrossRef - Seng, V., K. Abbaoui and Y. Cherruault, 1996. Adomian's polynomials for nonlinear operators. Math. Comput. Model., 24: 59-65.
CrossRef








