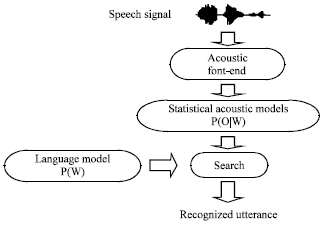
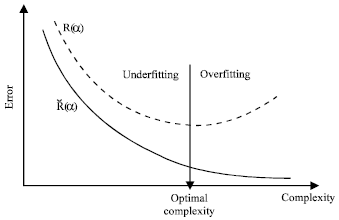
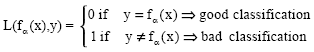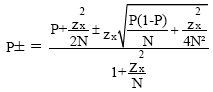Research Article
Towards Discriminative Training Estimators for HMM Speech Recognition System
Ecole Nationale d�Ingenieurs de Sfax, �ENIS�, Department of Genie Electrique, BP W, 3038, SFAX, Tunisia
Z. Ben Messaoud
Ecole Nationale d�Ingenieurs de Sfax, �ENIS�, Department of Genie Electrique, BP W, 3038, SFAX, Tunisia
A. Ben Hamida
Ecole Nationale d�Ingenieurs de Sfax, �ENIS�, Department of Genie Electrique, BP W, 3038, SFAX, Tunisia