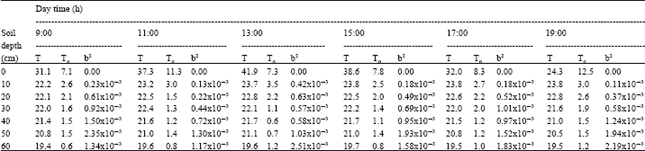
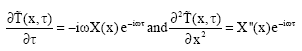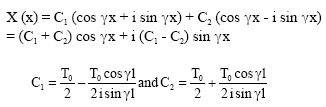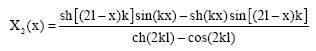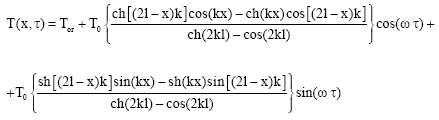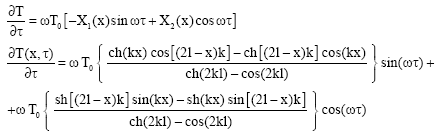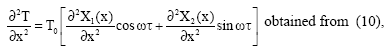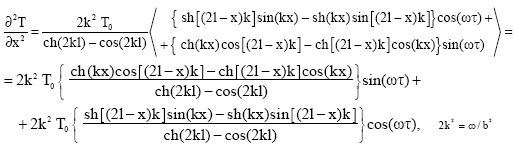Research Article
Determination of Initial Unconditional Solution of Heat Conductivity Equation for Evaluation of Temperature Variance in Finite Soil Layer
Department of Soil Science, Faculty of Agriculture Ondokuz May1S University, 55139 Samsun, Turkey