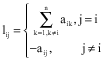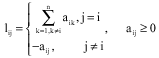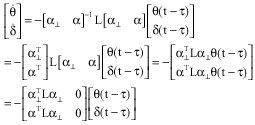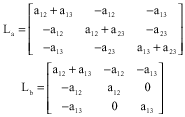Research Article
Optimal Weights for Consensus of Networked Multi-Agent Systems
Department of Control Science and Engineering, Huazhong University of Science and Technology, Wuhan 430074, China
Hua-Jing Fang
Department of Control Science and Engineering, Huazhong University of Science and Technology, Wuhan 430074, China