Research Article
Determining the Factors Affecting Efficiency Scores in Agriculture
Department of Agricultural Economics, Faculty of Agriculture, Adnan Menderes University, Aydin, Turkey
INTRODUCTION
As in other sectors, absolute measurement of efficiency and productivity is of great importance in the agricultural sector. If efficiency has not been achieved in production, detection and correction of the source of failure would minimize the potential economic loss. For the agricultural enterprises to realize sustainable production, it is necessary to determine their efficiency level and the factors affecting efficiency. Data envelopment analysis comes first among the classical methods used to evaluate the performance of decision- making units. Efficiency measurement with the method of data envelopment analysis is widely used in the agricultural sector as well. The measurement of efficiency, an important indicator used in the decision-making process, is widely used in production processes where different inputs and outputs are used together (Zhu, 2000; Sharma et al., 1999; Rahman, 2003; Tauer, 2001).
Majority of efficiency studies were focused on dairy farms. Baily et al. (1989) estimated efficiency on a sample of Ecuadorian dairy farms. They found a positive relationship between enterprises size and technical efficiency. In contrast to the New England study, medium sized Ecuadorian farms were found to be as allocatively efficient as large farms. Bravo-Ureta and Rieger (1991) examined efficiency of a sample of New England dairy farms, using the Stochastic Frontier Approach and Cobb-Douglas production function. They found overall economic inefficiencies of on average 30%. However it was little difference between technical and allocative efficiency. Mbaga et al. (2003) conducted a study in Canada, based on Cobb-Douglas type production functions. They reported that the mean herd size was 57.7 animals on Quebec dairy farms and the growth rate was 6.8%. Another important finding of this research was that DEA allowed for the easy performance of multiple output calculations on the basis of multiple inputs; it was found to be superior to the Stochastic Production Frontier analysis method. Lansink et al. (2002) studied technical efficiency of Finnish farms using data envelopment analysis. They reported that the conventional livestock farms had technical efficiency scores of 69%. Although DEA should not be used for comparison between different studies, since the scores only measure the relative efficiency within the sample (Coelli et al., 2002).
This study attempts to determine the factors affecting bounded continuous efficiency scores obtained through logistic regression method, in addition to the classical efficiency measurement.
THE MODEL AND DATA
Measurement of input and output amounts applied by the decision-making units of the enterprise for the economic decision is needed for the efficiency measurement of any production enterprise. This provides information on the efficiency of the production activities on the basis of a comparison between inputs and outputs. There are three types of efficiency, which are total efficiency, technical efficiency and scale efficiency. Technical efficiency is the success of obtaining maximum output by using the input composition in the most appropriate way. Technical efficiency allows one to compare between decision making units in terms of production maximization. The success of production on the right scale is called as scale efficiency. Total efficiency is obtained by multiplying technical efficiency and scale efficiency.
Mathematical basis of DEA dates back Farell (1957) who attempted to find out benefits of efficiency measurement and its application in practice. DEA is an efficiency measurement method first developed by Charnes et al. (1978, 1981) for the purpose of measuring relative efficiency of economic decision making units which are similar in terms of the products produced. In most simple terms, DEA is a non-parametric linear programming technique that measures the distance between the input and output values to the effective limit. When the relative efficiency of a unit is above the efficient limit on DEA, it means that the unit is efficient. When it is below this limit, it means the unit is inefficient (Amiteimoori and Kordrostami, 2005).
Assume each of I decision making unit consumes m different inputs, to produce outputs Let xij≥0 denote the inputs i consumed and yrj≥0 denote the output r produced by decision making unit j. Assume xij >0 and yrj >0 for some i and r for all j. Then the problem of DEA can be stated as:
(1) |
(2) |
Equation 1 is normalization constraint for each decision making unit. However, this problem will have infinite number of solutions. Since for different levels of virtual input, we will have different levels of virtual output. Thus, by imposing
Charnes et al. (1978) take a representative solution. The problem becomes maximizing the virtual output given a predetermined level of virtual input. Then the maximization problem will be:
(3) |
(4) |
| | (5) |
The solution to the above problem will be vectors Y and X, which will consist of μr s and vi s and finally z will be the efficiency score.
The calculated z scores were excepted as a dependent variable in logistic regression model. Dependent variable is generally integrated to the analysis in binary form in the logistic regression model which is widely used. In an alternative use of the logistic regression model, the dependent variable is continuous, but this alternative offers limited range (Manning, 1996).
The logistic regression model offers various virtues. Firstly it is easily transformed into a simple linear regression and secondly it yields predicted values within the natural boundaries of dependent variable. According to classical assumptions, ordinary least squares estimation of the logit model is also free of the heteroscedasticity problem caused by the use of using the logistic regression with bounded continuous data (Maddala, 1983).
S, which is between zero and unity and which is a function of a vector of dependent variables and X and some error term, ε, symmetrically distributed around zero are bounded continuous variables. When we apply the functional form of the logistic distribution on these variables, we obtain the following finding:
(6) |
Then we see that standard transformation then produces the simple linear regression equation:
(7) |
This study was conducted at 58 crop farms and 78 dairy farms which were selected from 6989 enterprises in Aydin-Turkey, by using randomly layer sampling method based on Eq. 8 (Yamane, 1967):
(8) |
| Where: |
| n | : | Sample size |
| N | : | Population size |
| Nh | : | Number of subjects in each layer |
| Sh | : | Standard deviation in each layer |
| D2 | : | Permitted error amount from the main mass mean d2/z2 d, where z shows the z value on the standard normal distribution table according to the error rate |
Crops produced by the crop farms are fig, olive, cotton, corn and wheat. Efficiency scores of the enterprises were found with DEA analysis. In DEA analysis, gross production was accepted as the sole output value. Four variables were taken as input. First and second input values applied were the variable costs used in the production. The third one is the labor used in the production. This includes the household labor and foreign labor as the value of input man work unit and this labor is assumed to work 300 days a year. In Man Work Unit, 0.50 coefficient was used for the age group 7-14; 0.75 coefficient was used for the women and 1.00 coefficient was used for men in age group 15-49; 0.75 coefficient for the men and 0.50 coefficient for the women in the age group 50 and above. The fourth input is the monetary value of the production areas for the crop farms and the monetary value of the
| Table 1: | Summary statistics for the output, inputs and DEA scores |
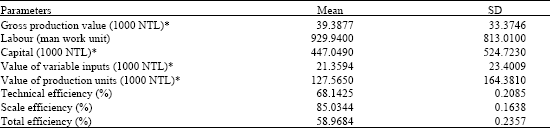 | |
| 1 US $ = 1.2732 New Turkish Lira (NTL) | |
total animal assets for the dairy farms. Definitive statistics concerning outputs and inputs and DEA scores are shown in Table 1.
At the first stage, efficiency scores of the enterprises were determined by the output oriented DEA (CCR). At the second stage, Logistic Regression Model was applied, by considering the efficiency scores obtained from DEA as the dependent variable in order to determine the effects of the various explanatory variables on efficiency. The model was used separately for total efficiency, technical efficiency and scale efficiency.
The DEA scores show the bounded and continuous structure between zero and unity. Therefore, the analysis of DEA scores was carried out by using the logistic regression method.
(9) |
The Eq. 3 was fitted by using the Gretl (Cottrell and Lucchetti, 2006).
(10) |
The variables which are thought to explain the efficiency scores in the model are as follows: age of the producer (X1: year), education period of the producer (X2: year), experience of the producer (X3: year), dummy variable (X4: 1 for the milk dairies, 0 for others) and enterprise scale (X5: 1 small scale enterprises, 2: bottom group medium scale enterprises, 3: top medium scale enterprises, 4: large scale enterprises). The model was developed primary for the purpose of revealing the extent to which the owner of the enterprise, general features of the enterprise can explain the technical efficiency, scale efficiency and total efficiency.
RESULTS AND DISCUSSION
Table 1 presents DEA scores of 136 agricultural enterprises, including 58 crop farms and 78 dairy farms. An analysis of these scores revealed that the technical efficiency was 70%, scale efficiency was 85% and total efficiency was 60% among the enterprises. According to these scores, it is necessary to reveal the factors affecting the technical efficiency in order to increase technical efficiency. For this purpose, estimations concerning to what extent features of the farm owner, scale of the enterprise affect the efficiency level of the crop farms and dairy farms are shown in Table 2. Findings of the logistic regression analysis indicate that the model explains the total efficiency by 60%. The extent to which the model can explain technical and scale efficiency is very low. Total efficiency level in the dairy farms was significantly higher than the crop farms. In addition, the finding that efficiency level decreases while enterprise scale increases was also found statistically significant. It is consistent with previous studies (Bravo-Ureta and Rieger, 1991; Tauer, 2001; Binici et al., 2006).
| Table 2: | The results of logistic regression for efficiencies |
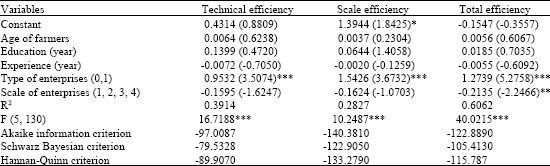 | |
| (t-statistics are in the parenthesis.) *: p<0.05, **: p<0.01, ***: p<0.001 | |
CONCLUSIONS
These findings indicate that conventional dummy variables such as age, education end experience do not constitute significant factors in explaining level of efficiency. The findings also reveal that small scale enterprises display a better performance than the large scale enterprises in terms of utilizing the resources. It is recommended that dairy production should be included in the production activity for the purpose of increasing efficiency of this enterprise in the region, since type of enterprises favors dairy production in terms of efficiency level.
ACKNOWLEDGMENT
I sincerely appreciate the help of our colleagues Altug Ozden and Suleyman Nizam during the field research.