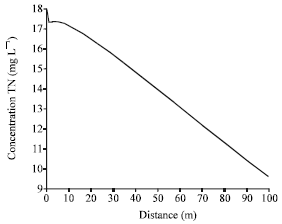
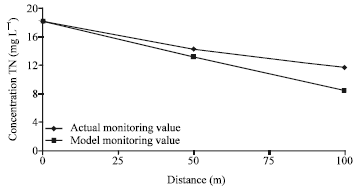
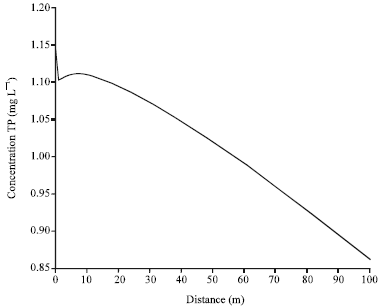
Research Article
The Research on Water Quality of Water Area around Drain Outlets of Longwangzui Sewage Plant in China
Department of Civil Engineering and Architecture,Wuhan University of Technology, Mail Box 169, West Mafang Shan Campus,No. 205 Luoshi Road, Wuchang 430070, Peoples Republic of China
LiveDNA: 964.28023