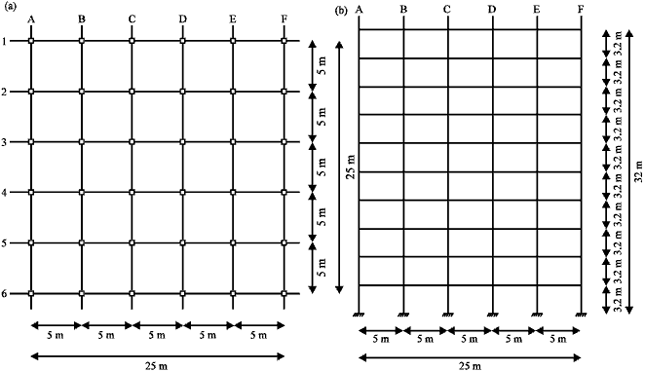
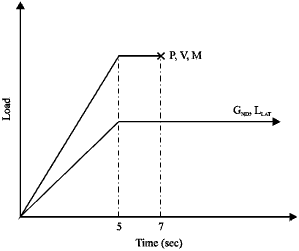
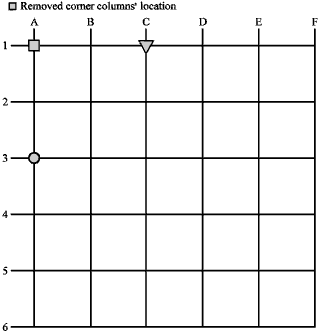
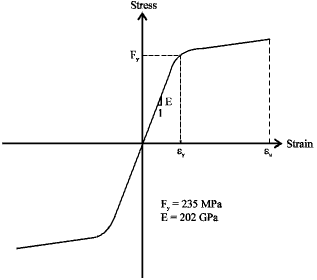
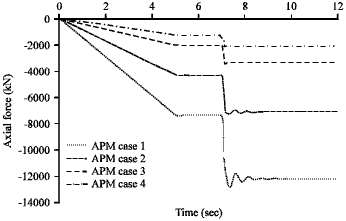
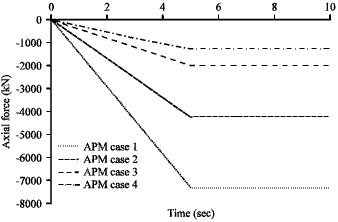
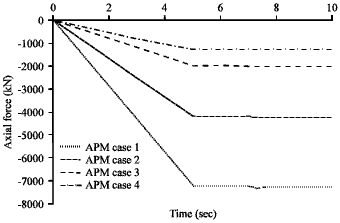
Research Article
Vulnerability Assessment of Progressive Collapse of Steel Moment Resistant Frames
Department of Civil Engineering, Faculty of Engineering, Lorestan University, Lorestan, Iran
Mojtaba Hosseini
Department of Civil Engineering, Faculty of Engineering, Lorestan University, Lorestan, Iran
Nader Fanaie
Department of Civil Engineering, K.N. Toosi University of Technology, Tehran, Iran