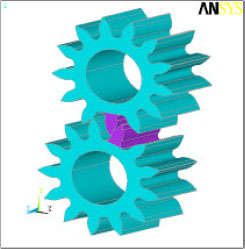
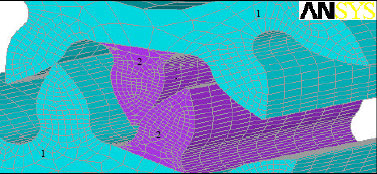
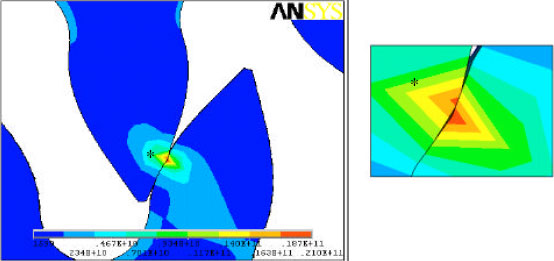
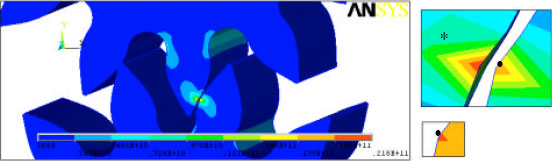
Research Article
Fatigue Analysis of Hydraulic Pump Gears of JD 1165 Harvester Combine through Finite Element Method
Deparment of Mechanic of Agricultural Machinery, University of Tehran, Karaj, Iran
A. Jafari
Deparment of Mechanic of Agricultural Machinery, University of Tehran, Karaj, Iran
S.S. Mohtasebi
Faculty of Engineering and Agricultural Technology, University of Tehran, Karaj, Iran
A.M. Setayesh
Department of Research and Development, ICM Company, Arak, Iran