Research Article
An Extended Kalman Filter Approach for Flux-Sensorless Control of a Linearized and Decoupled Induction Motor Drive
Department of Electrical and Electronic Engineering, Institute National Polythechnique Houphouet Boigny, BP 1093 Yamoussoukro, C�te d�Ivoire
S. Ouattara
Department of Electrical and Electronic Engineering, Institute National Polythechnique Houphouet Boigny, BP 1093 Yamoussoukro, C�te d�Ivoire
K.E. Ali
Department of Electrical and Electronic Engineering, Institute National Polythechnique Houphouet Boigny, BP 1093 Yamoussoukro, C�te d�Ivoire
Z. Yeo
Department of Electrical and Electronic Engineering, Institute National Polythechnique Houphouet Boigny, BP 1093 Yamoussoukro, C�te d�Ivoire
M. Koffi
Department of Electrical and Electronic Engineering, Institute National Polythechnique Houphouet Boigny, BP 1093 Yamoussoukro, C�te d�Ivoire











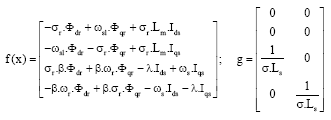
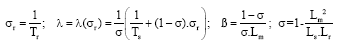
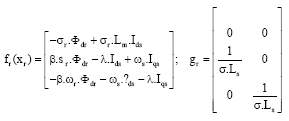


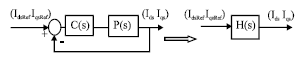
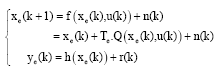
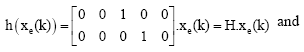
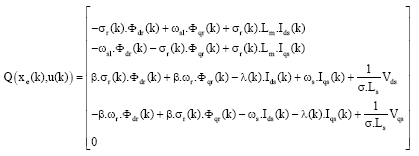
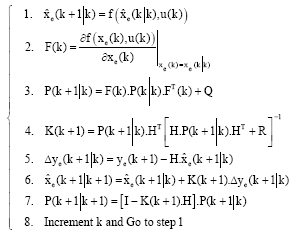
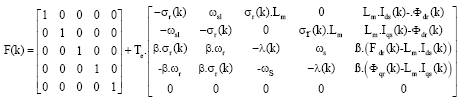
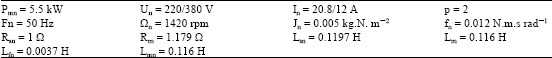
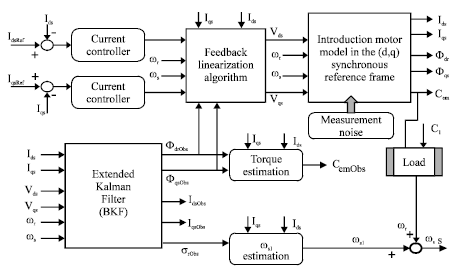
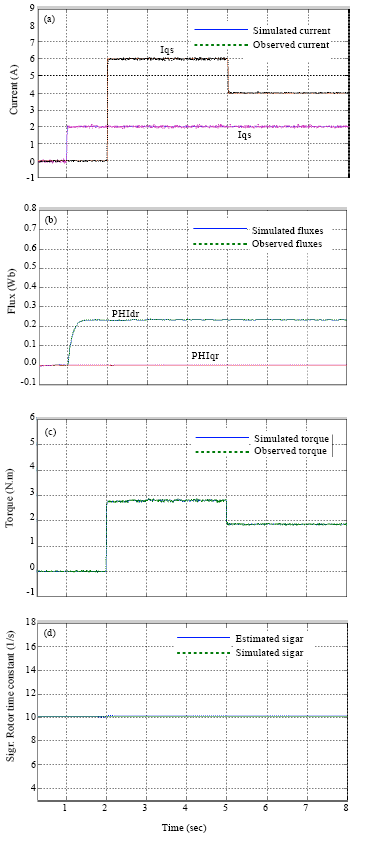
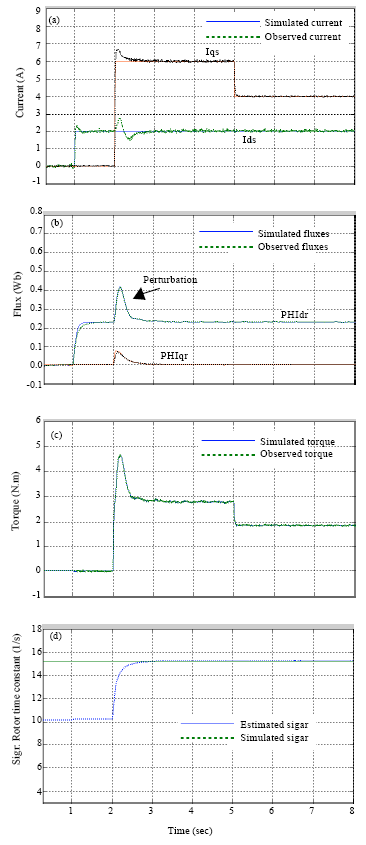
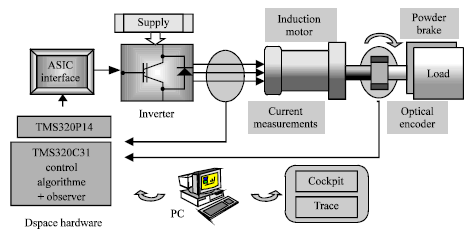
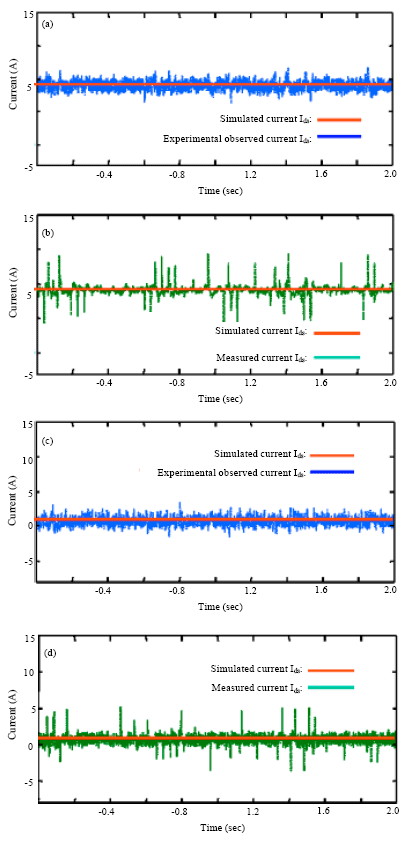
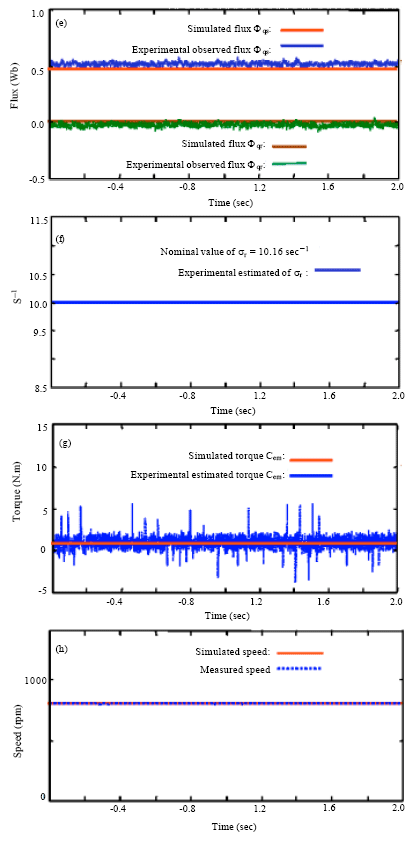
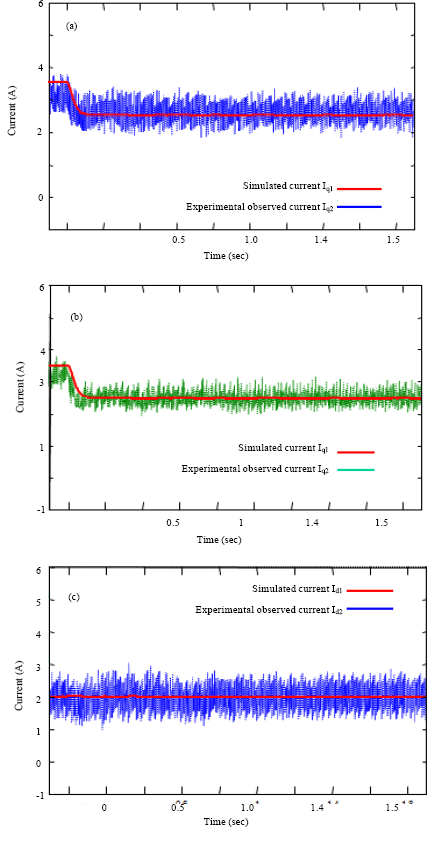
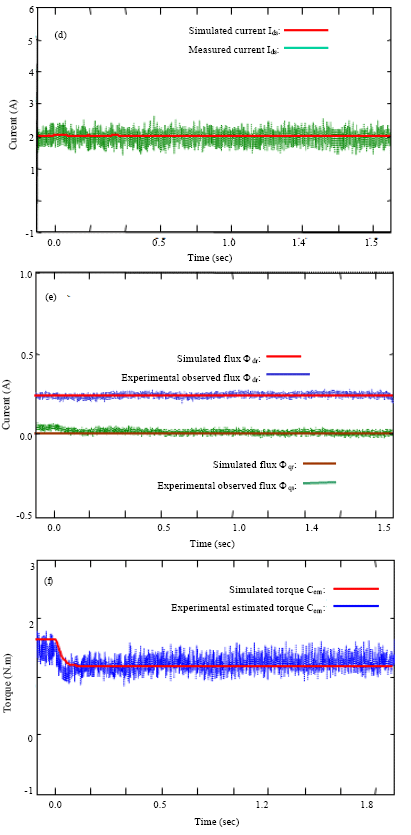
Alm Reply
thank you very much its a wonderfull site easy to use and usefull papers