On Modified Boubaker Polynomials: Some Differential and Analytical Properties of the New Polynomials Issued from an Attempt for Solving Bi-varied Heat Equation

INTRODUCTION

Through history, polynomials have been a very useful guide for mathematics, analytic theory of numbers and applied analysis (Bateman and Erdélyi, 1953; Guertz et al., 2000). The early works on polynomials can be attributed to Al-Khawarizmi (830) with his attempt to solve six canonical equations, followed by Omar Al-Khayyam (1050-1123) who tried to solves cubics geometrically by intersecting conics (Kiltz and Winterhof, 2006).

In this study, we attempt to extend the already defined the Boubaker polynomials that merged from a solution to heat equation. Once defined, registered and published, the Boubaker polynomials, as practical functional classes, were not considered and dealt with as an abstract mathematical object. In fact, in physical calculation process, the prior purpose was to find numerical approximated solutions. We present here to the worldwide scientific community, the modified Boubaker polynomials that are closer to mathematical analysis as long as they can be easily subjected to arithmetical and integral analysis.

MAIN CLASSICAL POLYNOMIALS

Classical polynomials have been defined by several methods according to their applications. Thus, as functional classes, they can be ranged according to the definition expression and its application. In this context, we can cite among others: the polynomials defined as solutions to differential equations, like Gegenbauer and Legendre polynomials, those defined by recursive formulae, like Fibonacci, Euler, Bessel and Bernoulli polynomials, those defined relatively to a set of values like Lagrange and Newton polynomials and finally the polynomials defined through trigonometric relations like the well-known Chebyshev polynomials

BOUBAKER POLYNOMIALS

Definition and Historic
The Boubaker polynomials were established for the first by Boubaker et al. (2006) as a guide for solving a one-dimensional formulation of heat transfer equation:

(1)

defined in the domain D, defined by Eq. 2:

(2)

The Boubaker polynomials have the demonstrated (Boubaker, 2007) explicit form:

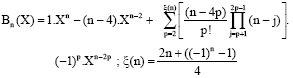(3)

According to this definition, the first Boubaker polynomials were (ONPDA, 2007):

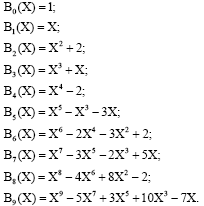(4)

The Modified Boubaker Polynomials
Definition
The Boubaker polynomials were tested and submitted to several studies from 2003 to 2007. Nevertheless they seemed not to be solution to any regular differential equation of the kind:

(5)

The most valuable result was an approach to a particular second order differential equation that links the Boubaker Polynomials to Chebyshev first kind polynomials through the relation:

(6)

At this stage, several expert colleagues advised us to propose a new form of the Boubaker polynomials, which fits better Eq. 6 and thus can yield a proper differential equation. After several tests and trials, we set the new proposed polynomials, which are the modified Boubaker polynomials defined mainly by Eq. 7:

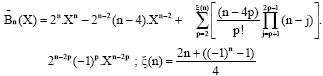(7)

According to this definition, the first modified Boubaker polynomials are:

(8)

The Modified Boubaker Polynomials Properties
The Modified Boubaker Polynomials Characteristic Differential Equation
Oppositely to the early defined Boubaker polynomials, the modified Boubaker polynomials are solution to a second order characteristic equation:

(9)

where T_n(X), for n>2, are the Chebyshev (1947) first order polynomials

The Modified Boubaker Polynomials Graphical Representation

The graphics of first modified Boubaker polynomials are presented in Fig. 1 and 2:

The Modified Boubaker Polynomials Quasi-polynomial Expression:

Thanks to relations given by Eq. 6 and 7, we were able to establish a quasi-polynomial expression of the modified Boubaker polynomials:

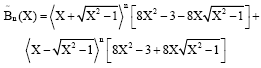(10)

or by setting:

(11)

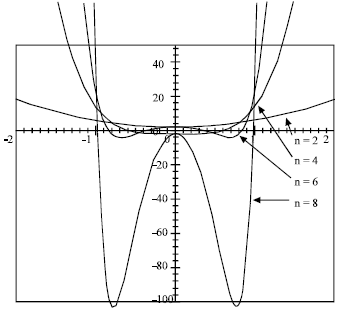Fig. 1:	Modified Boubaker polynomials (first even orders)

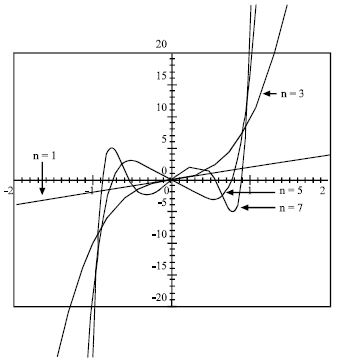Fig. 2:	Modified Boubaker polynomials (first odd orders)

so that:

(12)

we obtain simplified relation, Eq. 13:

(13)