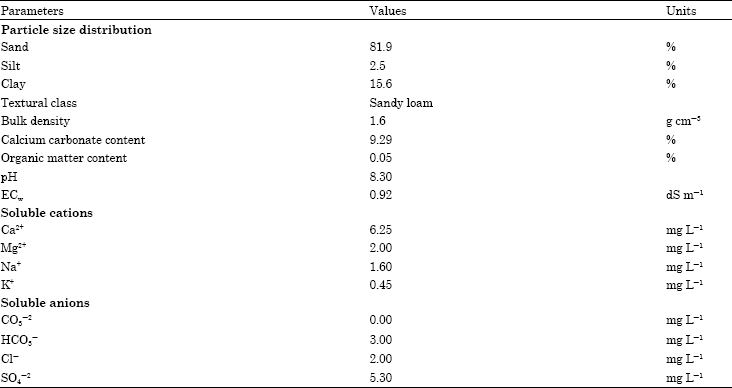
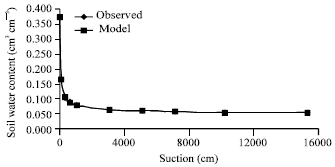
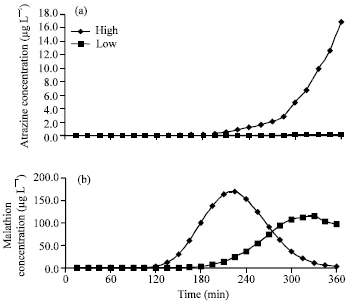
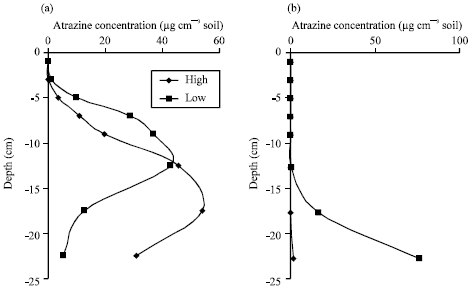
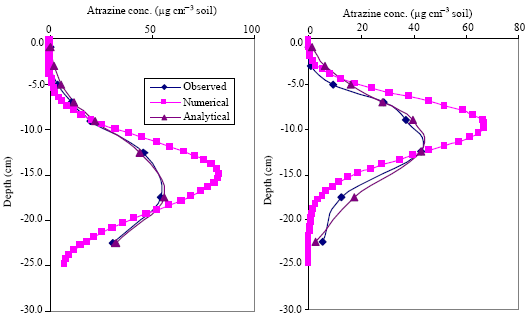
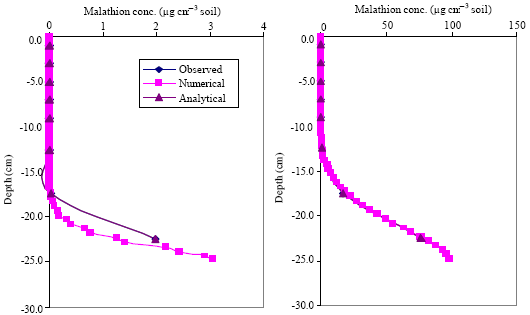
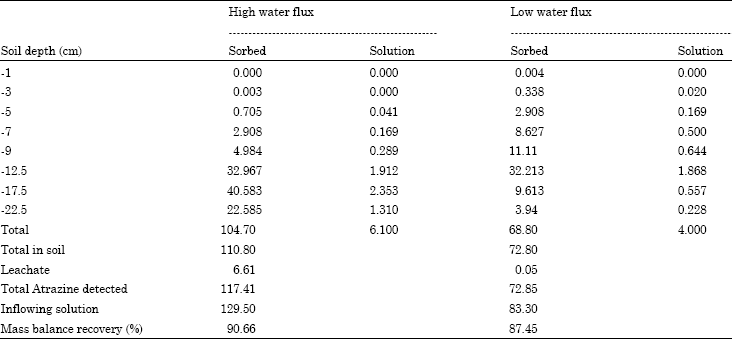
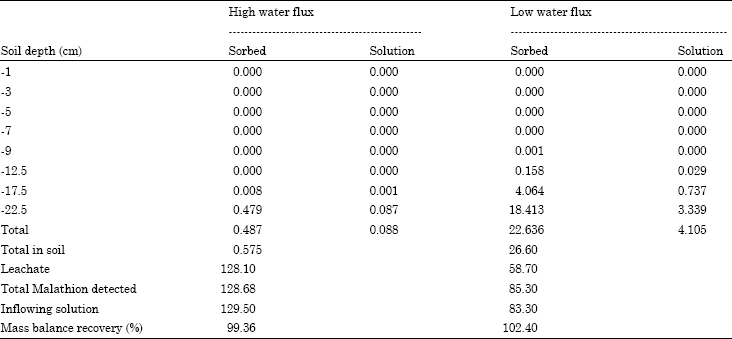
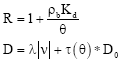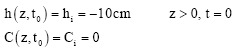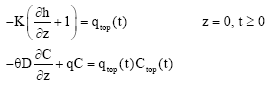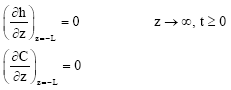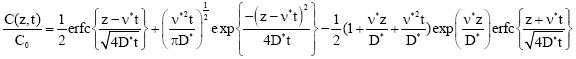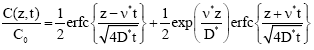Research Article
Behavior of Atrazine and Malathion Pesticides in Soil: Simulation of Transport Process using Numerical and Analytical Models
Dapartment of Soil Science, College of Food and Agricultural Sciences, King Saud University, P.O. Box 2460, Riyadh 11451, Saudi Arabia
A.M. Al- Turki
Dapartment of Soil Science, College of Food and Agricultural Sciences, King Saud University, P.O. Box 2460, Riyadh 11451, Saudi Arabia
M.I. Al- Wabel
Dapartment of Soil Science, College of Food and Agricultural Sciences, King Saud University, P.O. Box 2460, Riyadh 11451, Saudi Arabia
M.H. El- Saeid
Dapartment of Soil Science, College of Food and Agricultural Sciences, King Saud University, P.O. Box 2460, Riyadh 11451, Saudi Arabia