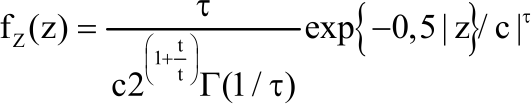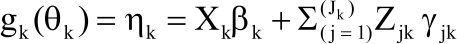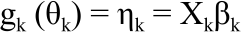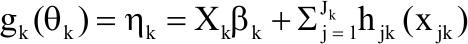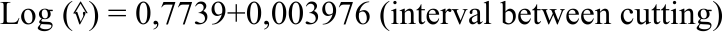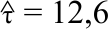Research Article
Using an Algorithm to Fit a GAMLSS Model on Dry Matter Data from Brachiaria brizantha
Faculty of Forestry and Environmental Engineering, Universidad Nacional de Jaén, Cajamarca, Peru
LiveDNA: 58.34881
Nora Valbuena Torres
Agricultural and Marine Sciences Program, Universidad Nacional Experimental de los Llanos Occidentales Ezequiel Zamora, Guanare, Venezuela
Manuel Milla Pino
Faculty of Civil Engineering, Universidad Nacional de Jaén, Cajamarca, Peru
Martín Grados Vásquez
Agricultural and Marine Sciences Program, Universidad Nacional Experimental de los Llanos Occidentales Ezequiel Zamora, Guanare, Venezuela
Ydalia Velásquez Casana
Graduate School, Universidad Nacional de Trujillo, Peru
Erick Delgado Bazan
Faculty of Civil Engineering, Universidad Nacional de Jaén, Cajamarca, Peru
César Osorio Carrera
Graduate School, Universidad César Vallejo, Peru
Ricardo Shimabuku Ysa
Faculty of Mechanical and Electrical Engineering, Universidad Nacional de Jaén, Cajamarca, Peru
River Chávez Santos
Faculty of Economic and Administrative Sciences, Universidad Nacional Toribio Rodríguez de Mendoza de Amazonas, Peru
Luis Ramírez Calderón
Graduate School, Universidad César Vallejo, Peru
Clelia Jima Chamiquit
Faculty of Health Sciences, Universidad Nacional Toribio Rodríguez de Mendoza de Amazonas, Peru