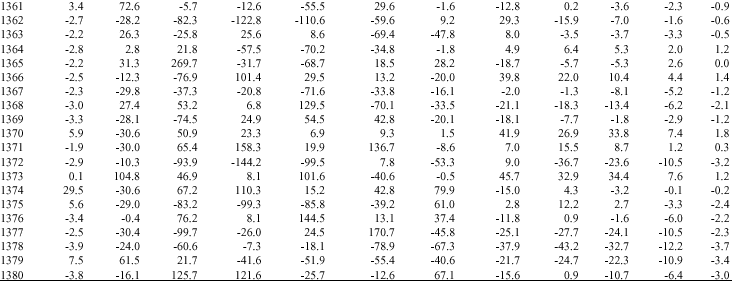
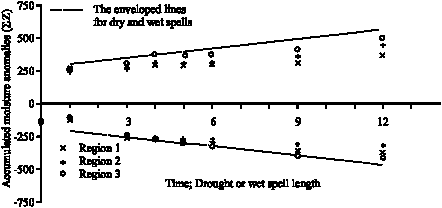
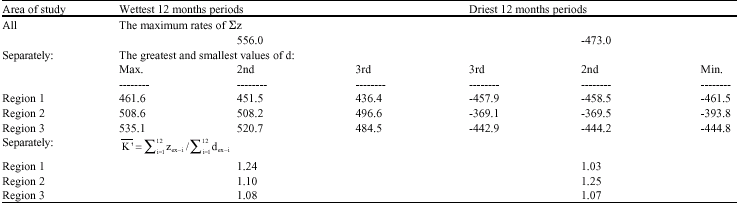
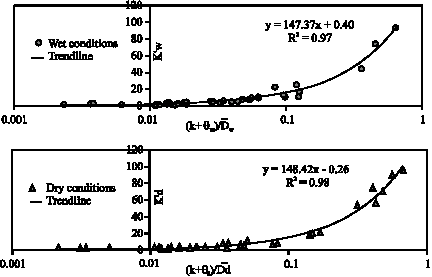
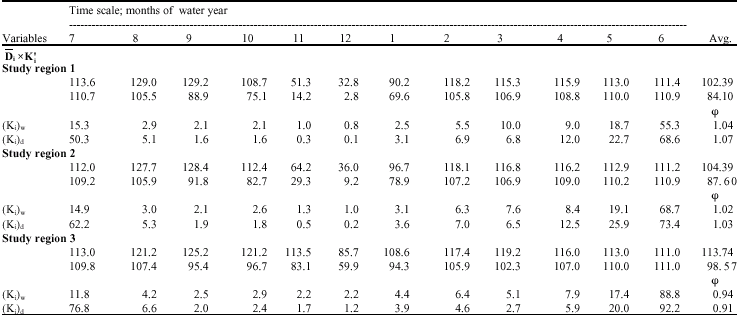
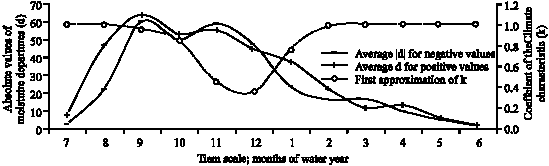Research Article
The Scaling Technique in Palmer Drought Severity Index; Generalized Calibration and Modification
Department of Agricultural Engineering-Water, Agricultural College, Shiraz University, Shiraz, Islamic Republic of Iran
Sefollah Amin Sichani
Department of Agricultural Engineering-Water, Agricultural College, Shiraz University, Shiraz, Islamic Republic of Iran
Saied Mohammad Jafar Nazemossadat
Department of Agricultural Engineering-Water, Agricultural College, Shiraz University, Shiraz, Islamic Republic of Iran
Mohammad Karamouz
Department of Civil Engineering, Engineering College, Tehran University, Tehran, Iran
Soheila Javanmard
Department of Atmospheric Sciences and Meteorological Research Center, Pazhuhesh City, Tehran, Iran