ABSTRACT
Use of an event scale MUSLE model for obtaining accurate long-term annual sediment yield estimates from micro-watersheds was evaluated. Such estimates are extremely important for designing appropriate soil/ water conserving measures. For easy extraction and inputting of model input parameters, the proposed model was interfaced to an Arc-View/Spatial Analyst geographic information system. Application of this GIS interfaced MUSLE model on two gauged (pine and oak forest) hilly micro-watersheds viz., Salla Rautella (0.47 km2) and Naula (0.42 km2), in Almora district of Uttaranchal, India showed that it could estimate annual sediment yields with absolute mean relative errors ranging between 12-14%. Even long-term average sediment yields for Salla Rautella (observed: 9.58 tons and estimated: 10.92 tons) and Naula: (Observed: 23.89 tons and estimated: 26.61 tons) micro-watersheds could be quite realistically simulated by the proposed model.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/pjbs.2008.270.274
URL: https://scialert.net/abstract/?doi=pjbs.2008.270.274
INTRODUCTION
Soil erosion, continues to be a global constraint to economic development. Despite decades of efforts to arrest soil erosion, many farmers are reluctant or unable to adopt appropriate land-use practices. Often these practices fail to combine high productivity, increased soil fertility, reduced soil erosion and enhanced welfare. Still, soil conservation is proposed as a viable route to obtain these objectives (Ekbom 1998). The negative changes in soil quality is a worldwide concern, especially in developing countries where soil erosion is becoming a limiting factor in increasing or even sustaining agricultural production. Heenrink et al. (2001) describe that 38% of the world`s agricultural land is degraded, while in Africa and Central America, the share of degraded land in total agricultural land is as high as 65 and 74%, respectively. South America`s agricultural degraded land is around 45%.
It is estimated that in India out of a total geographic area of 328 million hectare, about 187 million hectare are subject to varying degrees of water erosion problems (Anonymous, 1996). It has been observed that the trap efficiency of Indian reservoirs is about 90%. The heavy sedimentation of these reservoirs/dams has not only resulted into drastic reduction in their live storage capacity but also resulted into a reduction of their lifespan and carrying capacity to just 1/4th of what was assumed at the time these were designed thereby leading to an equally alarming situation of serious floods in the country. Floods hit India almost every year. It has been estimated that about 5334 million tones of soil is lost annually due to runoff and associated activities thereby leading to an annual average national soil erosion rate of about 16.75 t ha-1 year-1 against the permissible level of 7.5 to 12.5 tones for various regions (Bhan, 1997). Further, it has been assessed that annually about 8.4 metric tones of soil nutrient lost due to soil erosion problem are much greater than the quantity we are using at present in Indian agriculture (Singh and Poonia, 2003). Due to this, in terms of annual food grain production, soil erosion accounts for a total productivity loss of about 40 million tones. Thus, accurate soil loss estimates are extremely important for designing appropriate resource managing and soil/water conserving measures.
Well-validated watershed scale hydrologic models are excellent predictive tools for obtaining accurate sediment yield estimates from agro-ecologically diverse watersheds. In this context Universal Soil Loss Equation (USLE) (Wischmeier and Smith, 1978), due to its dependence on easily available soil, topographic and vegetation data, has emerged as the most commonly used soil loss estimating model. As USLE predicts gross soil loss, it needs to be multiplied by a sediment delivery ratio to give sediment yield estimates. It has been shown that delivery ratios for determining sediment yields from soil loss predictions suffer from uncertainty due to considerable variations in rainfall distributions with time. Due to uncertainty in delivery ratio and inability of USLE model to give direct sediment yield estimates, Modified Universal Soil Loss Equation (MUSLE) was proposed by Williams and Berndt (1977). However, in contrast to USLE, MUSLE model has been generally used to predict sediment yields on single storm basis. Although there are some reports that it can also be used to predict sediment yields on annual basis by determining soil loss for events at varying return periods (Simons and Senturk, 1992). Yet, it has not been widely applied for obtaining long term annual sediment yield estimates. Further, it is observed that USLE model generally gives highly overestimated soil loss for small sized drainage basins (Weggel and Rustom, 1992). However whether the same holds true for the MUSLE model also has not been tested widely.
Thus with this in background the present investigation was mainly aimed at Testing long term annual sediment yield estimating potential of MUSLE model on two hilly micro-watersheds in Almora district of Uttaranchal, India.
MATERIALS AND METHODS
To meet the proposed objective two gauged micro-watersheds viz., Salla Rautella (0.47 km2) and Naula (0.42 km2), with continuous rainfall and discharge records for 6 years (i.e., 1991-93 and 1996-98), were selected. These micro-watersheds, extending between 29°35’05” N to 29° 35’30” N latitudes and 79°33’10” E to 79°33’ 33” longitudes, are situated about 32-38 km northwest of Almora town of Uttaranchal (Fig. 1a). Dense (reserved) pine (Pinus roxburghii) and oak (Banj sp.) forests are the major land use types for the Salla Rautella and Naula micro-watersheds, respectively. Their absolute relief and average slope are about 1650 and 2190 m above m.s.l. and 26.4° and 25.0°, respectively. The soils of these test watersheds are in general of sandy loam to loamy sand texture with average organic matter content of 0.74-1.40%, saturated hydraulic conductivity of 134-235 mm h-1 and volumetric soil moisture contents at field capacity and saturation as 15 and 30%, respectively (Kaur et al., 2002). In general, the climate of this region is sub-temperate with moderate summers (18-22°C), a short spell (about 2 months) of chilling winter and general dryness, except during southwest monsoon season. Average annual rainfall for the Salla Rautella (Pine forest) and Naula (Oak forest) micro-watersheds stands at 927 and 981 mm, respectively (Rawat et al., 1999).
MUSLE model input data generation: The sediment yield (Y, tones) in Modified Universal Soil Loss Equation (MUSLE) is in general expressed as (Williams and Berndt, 1977):
(1) |
| Where: |
| Q | = | Total runoff volume (in m3) |
| qp | = | Peak runoff rate in (m3 sec-1) |
| K | = | Soil erodibility factor |
| LS | = | Slope length and gradient factor |
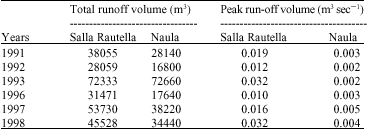
| Table 1: | Annual total run-off volumes and peak run-off rates for Salla Rautella (Pine forest) and Naula (Oak forest) micro-watersheds |
 | |
C=Cropping management factor | |
These input parameters were estimated as per the following procedures.
Run-off volume (Q) and peak run-off rate (qp) estimation: Annual run-off volume (Q, m3) and peak runoff rate (qp, m3 sec-1) for 1991-93 and 1996-98 years was obtained from weekly stage hydrograph data obtained through water level stage recorder installed at the mouth of each watershed (Rawat et al., 1999). The annual total run-off and peak run-off rates for Salla Rautella (Pine forest) and Naula (Oak forest) micro-watersheds was show in Table 1.
Soil erodibility factor (K) estimation: The soil erodibility factor (K) represents average soil loss from a specific area of soil in cultivated continuous fallow with a standard plot length as 22.13 meters and a standard percentage slope as 9%. It varies from 0.70 for the most fragile soil to 0.01 for the most stable soil. The K factor was determined through a particle size, organic matter, soil structure and permeability data based soil erodibility nomograph (Johnson et al., 1984). The following formula was used to evaluate the nomograph readings:
(2) |
| Where: |
| M | = | particle size diameter = {(%silt + %very fine sand)x(100 - %clay)} |
| a | = | Percent organic matter |
| b | = | Soil structure code |
| c | = | Profile permeability class |
In the present study, the above %sand, %silt, %clay, %organic matter, soil structure and soil permeability data for the test watersheds (Table 2) were obtained from Kaur et al. (2002).
GIS based topographic factor (LS) estimation: The slope length and gradient factor (LS) is defined as the ratio of soil loss from any slope length and gradient to soil loss
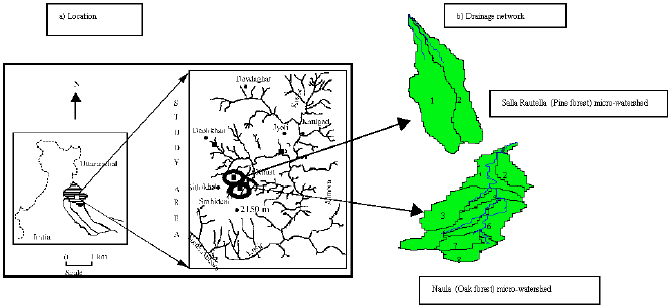 | |
| Fig 1: | Location of test Salla Rautella (Pine forest) and Naula (Oak forest) micro-watersheds and their drainage networks |
| Table 2: | General soil characteristics of test micro-watersheds |
 | |
from a 22.13 m plot with 9% slope and same soil type and other conditions. It varies from 0.1 to 5 in the most frequent farming contexts in West Africa and may reach 20 in mountainous areas. This factor is defined by the multiplication of the L and S-factors (Moore and Burch, 1986), where:
(3) |
Here, Lai is the mean overland flow length (in m) of an ith order test watershed and is computed probabilistically (Rodriguez-Iturbe and Valdes, 1979), based on the GIS interface derived total watershed area, its stream number, order and length, in the following manner:
(4) |
| Where: |
| A | = | Test watershed area (in m2), PoAi (i.e., initial state probability) is the probability of a raindrop to (initially) fall on an ith order overland region and is equal to the ratio of the total area of ith order overland region to the total watershed area |
| Ni | = | No. of ith order streams |
| Lci | = | Mean ith order channel length (m) and m is a slope dependent exponent computed as (McCool et al., 1989) |
(5) |
Where, θ = slope of test watershed in degrees = tan-1 (watershed slope in %/100). While, slope gradient (S) factor was computed as
(6) |
| Where: |
s = Mean slope (in %) of test watersheds
In the present study, this topographic data for each test watershed was obtained through avenue programming of above procedures in an Arc View/Arc View Spatial Analyst interface (ESRI, 1999). For this, firstly the two micro-watersheds and their sub-watersheds and drainage networks were digitally delineated from the test area`s digital elevation model (Kaur and Dutta, 2002). Figure 1b gives a pictorial depiction of the delineated test watersheds and their drainage networks. Each sub
| Table 3: | GIS interfaced geomorphologic parameters Salla Rautella and Naula micro-watersheds |
 | |
| Table 4: | Observed VS MUSLE model simulated sediment yields for Salla Rautella and Naula micro-watersheds |
 | |
watershed within any test watershed was identified by the order of the stream flowing through it. Streams were ordered as per Strahler`s (1952) stream ordering method. Table 3 shows these GIS interface derived geomorphologic parameters for the two test micro-watersheds.
Crop management and conservation practice factor (CP) estimation: The cropping management factor (C) represents the ratio of soil loss from land with specific cropping and management to that from tilled and fallow conditions on which the K factor is evaluated. The C-factor, also called the cover and management factor, generally varies from 1 for bare soil to 1/1000 for forest, 1/100 for grasslands and cover plants and 1 to 9/10 for root and tuber crops. The erosion-control-practice factor (P), on the other hand, represents the effect of conservation practices. The P factor is determined as the ratio of soil loss using one of the conservation practices to the soil loss using straight row farming. The P factor for straight row farming is always equal to unity. It generally varies from 1 for bare soil with no erosion control to about 1/10 for tied ridging on a gentle slope.
In the present study, average CP-factors for the two micro-watersheds were determined through inverse modelling on annual hydrologic and sediment yield records for 1991 and 1992. This resulted into CP values of 0.008 and 0.03 for the Salla Rautella and Naula micro-watersheds, respectively. As the two test watersheds with pine and oak forests had no conservation practices, therefore the above CP values can also be treated as C-factor values for the two test watersheds. These crop management factor values, obtained through inverse modelling technique, for the two test watersheds were found to be quite close to those given by Jianguo (2001) for the mixed pine and oak tree (coniferous) -forests.
MUSLE model validation and evaluation: The sediment yields estimated through above procedures were validated on four years (i.e., 1993 and 1996-1998) annual sediment yield records for Salla Rautella (Pine forest) and Naula (Oak forest) micro-watersheds. Long term annual sediment yield estimating potential of MUSLE model on micro-watersheds was evaluated in terms of mean relative errors (Green and Stephenson, 1986). Relative Errors (RE) were expressed as:
(7) |
| Where: |
| S | = | MUSLE simulated sediment yield (tons) |
| O | = | Observed sediment yield (tons) |
RESULTS AND DISCUSSION
Long term annual sediment yield estimates through MUSLE: The above analysis showed that Salla Rautella is first order micro-watershed while Naula is second order micro-watershed (Table 3). It was further observed that as expected Naula micro-watershed, with higher LS-factor value (28.71) than Salla Rautella micro-watershed (25.40), was associated with higher sediment yields (Table 4). It could be clearly observed from Table 4 that MUSLE model estimated sediment yields were associated with about (-) 12 to 14% overall mean relative errors. Comparison of actually observed mean and standard deviation values for annual sediment yields from test micro-watersheds (i.e., Salla Rautella: mean = 9.58 tons; STD = 4.10 tons and Naula: mean = 23.89 tons; STD = 5.10 tons) with their corresponding simulated values (i.e., Salla Rautella: mean = 10.92 tons; STD = 4.67 tons and Naula: mean = 26.61tons; STD = 6.37 tons) further showed that long term annual sediment yields could be quite realistically simulated by the MUSLE model. The present study could thus clearly show that MUSLE model can give accurate long-term average annual sediment yield estimates for micro-watersheds.
CONCLUSIONS
In Indian, there are about 3297 watersheds, of which about 70% are un-gauged of remaining 30% watersheds that are gauged, very few have functional gauging stations. As most of the Indian watersheds are un-gauged or inadequately gauged, therefore a successful application of the MUSLE model for long-term annual sediment yield estimation on two Indian micro-watersheds in fact projected its tremendous application potential for the evolution of a decentralized planning process, at micro-watersheds scales, in the country.
REFERENCES
- Heenrink, N., A. Kuyvenhoven and M.S. Van-Wijk, 2001. Economic Policy Reforms and Sustainable Land Use in Developing Countries: Issues and Approaches. In: Economic Policy and Sustainable Land Use: Recent Advances in Quantitative Analysis for Developing Countries, Heerink, N., H. Van-Keulen and M. Kuiper (Eds.). Physica-Verlag, New York.
- Kaur, R., K. Sanjeev, H.P. Gurung, J.S. Rawat, A.K. Singh, P. Shiv and R. Geeta, 2002. Evaluation of pedo-transfer functions for predicting field capacity and wilting point soil moisture contents from routinely surveyed soil texture and organic carbon data. J. Indian Soc. Soil Sci., 50: 205-208.
Direct Link - Rodriguez-Iturbe, I. and J.B. Valdes, 1979. The geomorphological structure of hydrologic response. Water Resour. Res., 15: 1409-1420.
CrossRefDirect Link - Strahler, A.N., 1952. Dynamic basis of geomorphology. Bull. Geol. Soc. Am., 63: 923-938.
CrossRefDirect Link - Weggel, J.R. and R. Rustom, 1992. Soil erosion by rainfall and runoff-state of the Art. Geotextiles Geomembr., 11: 551-572.
CrossRef - Williams, J.R. and H.D. Berndt, 1977. Sediment yield prediction based on watershed hydrology. Trans. ASAE, 20: 1100-1104.
Direct Link








