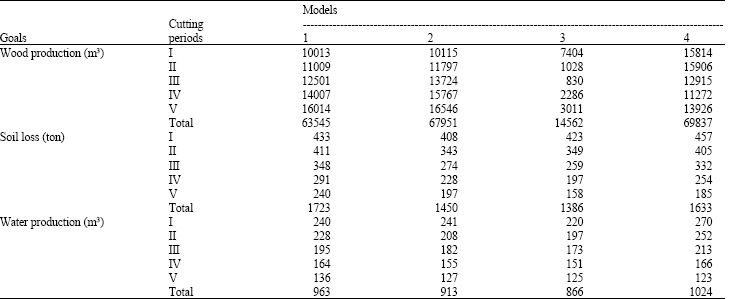
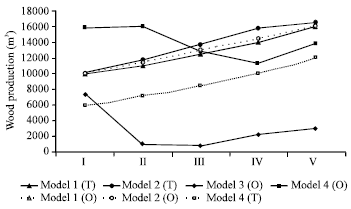
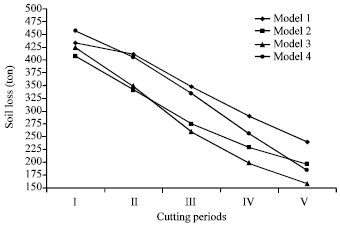
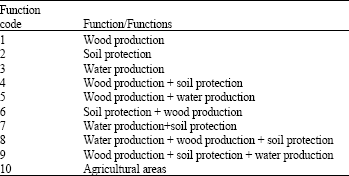
Research Article
Developing a Multi-Objective Forest Planning Process with Goal Programming: A Case Study
Faculty of Forestry, Karadeniz Technical University, 61080 Trabzon, Turkey
Mehmet Misir
Faculty of Forestry, Karadeniz Technical University, 61080 Trabzon, Turkey