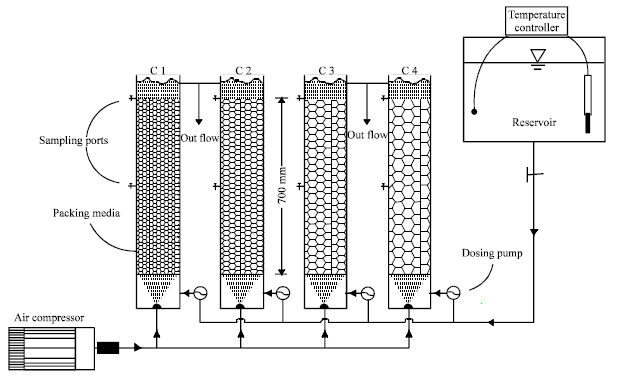
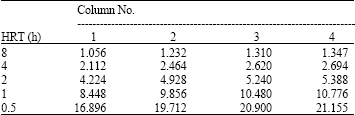
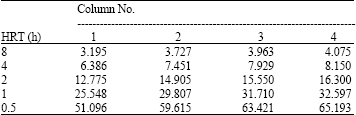
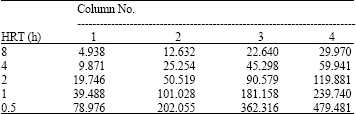
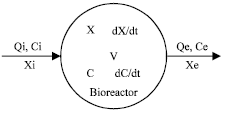
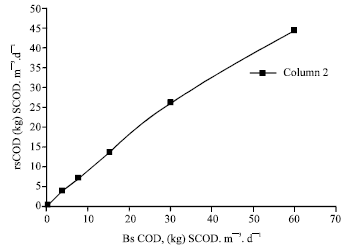
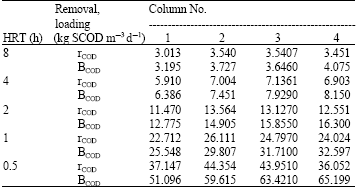
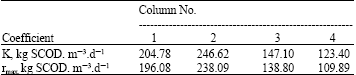
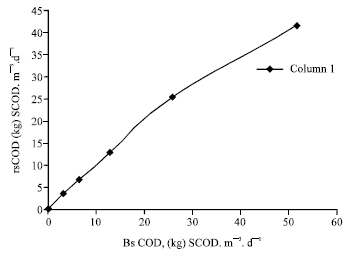
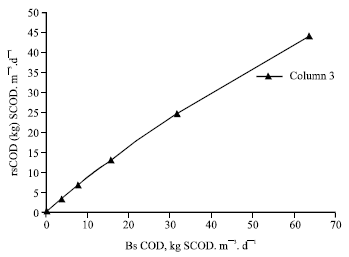
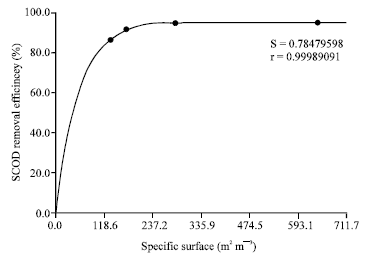
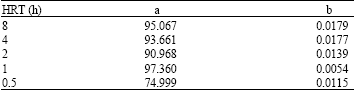
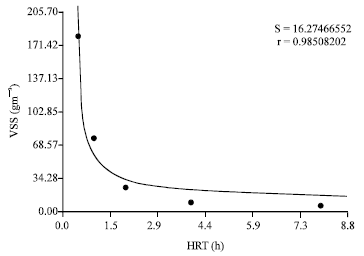
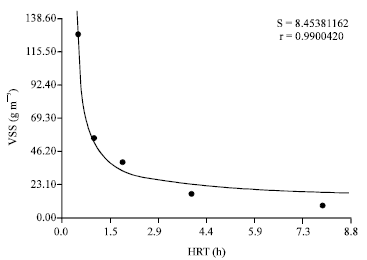
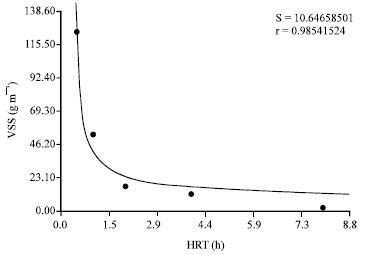
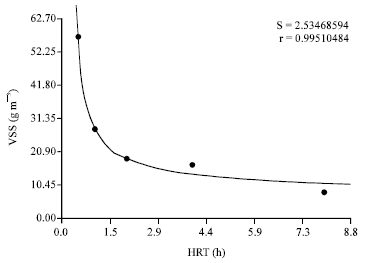
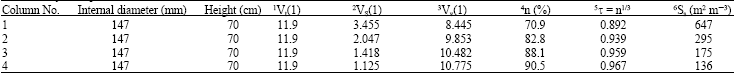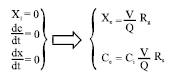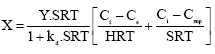Research Article
Evaluation of Operation of Submerged Aerated Filters in Wastewater Treatment and Excess Sludge Production
Civil Engineering College, Iran University of Science and Technology, Tehran, Iran
Ibrahim Jabbari
Civil Engineering College, Iran University of Science and Technology, Tehran, Iran