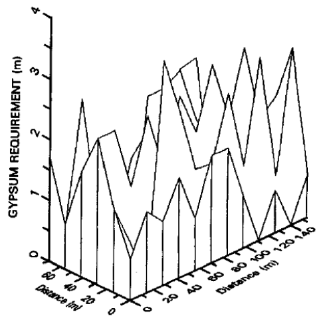
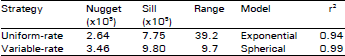Research Article
Patterns in Gypsum Requirement Before and After Gypsum Application
Department of Soil Science, NWFP Agricultural University, Peshawar
Ahmad Bakhsh
Agricultural Research Institute, Dera Ismail Khan, Pakistan
Akbar Hussain Gurmani
Agricultural Research Institute, Dera Ismail Khan, Pakistan